C применением кодов Хаффмана
Кафедра 308
Лабораторная работа №2
на тему: «Методы сжатия изображений»
по дисциплине
«Обработка аудио- и видеоинформации»
Вариант 5
Студент:
Группы № 03-518
Шпилевой С.Г.
Преподаватель:
Доцент, к.т.н.
Максимов А.Н.
Москва 2013
Задание
1) Провести «вручную» сжатие 2-ух фрагментов данных методом группового кодирования. Сравнить полученные коэффициенты сжатия.
2) Провести «вручную» сжатие 2-ух фрагментов данных методом LZW. Сравнить полученные коэффициенты сжатия.
3) Провести «вручную» сжатие 2-ух фрагментов данных с применением кодов Хаффмана. Сравнить полученные коэффициенты сжатия.
4) Провести «вручную» сжатие 2-ух фрагментов данных с применением алгоритмов RLE, LZW и кодов Хаффмана. Описать полученные результаты и сделать соответствующие выводы.
5) Реализоваь алгоритм JPEG в среде Mathcad и применить его для сжатия двух фрагментов изображения согласно варианту задания при q=2 для 1-ого фрагмента и при q=2 и 7 для 2-ого фрагмента. Сравнить полученные коэффициенты сжатия и объяснить результаты. Сделать вывод о влиянии пиксельных значений исходных фрагментов изображения на эффективность сжатия.
Исходные данные
| Номер задания | |||||
| 1 (RLE) | 2 (LZW) | 3 (Haffman) | 4 (все три метода) | 5 JPEG | |
| Вариант 5 | 1,2 | 5,8 | 11,10 | 21,26 |
Практическая часть
Сжатие «вручную» 2-ух фрагментов данных
Методом группового кодирования
Алгоритм группового кодирования известный в англоязычной литературе как RLE – Run Length Encoding является самым простым и, как следствие, самым быстрым и нетребовательным к ресурсам ЭВМ. Его идея предельно проста: если во входном потоке данных встречаются повторяющиеся группы символов (байтов), то в выходной (сжатый) поток записываются лишь число символов в группе и сам повторяющийся символ.
1) Исходная строка символов:
bbbbbbbccccccbbcaaaaaaabbbccccaaaaaaabbbbbaaaaadddddddddaaaadd
Исходная строка символов после кодирования будет иметь вид:
7b6c2b1c7a3b4c7a5b5a9d4a2d
Так как исходная строка занимала 62 байта, а кодированная – 26 байт, то в результате достигается коэффициент сжатия Kсж = 62/26 = 2,385 > 1, следовательно,сжатие считается эффективным.
2) Исходная строка символов:
cbcbbbbcdccddaddabbddccaaaccddddccbbbaaadddddbbbbcacccddaabb
Исходная строка символов после кодирования будет иметь вид:
03cbc4b02cd2c2d1a2d1a2b2d2c3a2c4d2c3b3a5d4b02ca3c2d2a2b
Так как исходная строка занимала 60 байт, а кодированная – 55 байт, то в результате достигается коэффициент сжатия Kсж = 60/55 = 1,09 > 1, следовательно, сжатие считается эффективным.
Сжатие «вручную» 2-ух фрагментов
Данных методом LZW
LZW относится к группе словарных методов сжатия, которые разбивают входной поток данных на слова. Словом называется последовательность символов (байт). Совокупность всех слов называется словарем, в котором каждое слово содержится под своим номером (индексом, ссылкой). В выходной поток записываются только ссылки. Эффект сжатия возникает за счет того, что длина ссылок, как правило, меньше длины слов. Словарь формируется итеративно, по ходу работы алгоритма сжатия/распаковки.
5) b | a | a | c | c | b | cc | bc | a | ba | cc | ab | ba | ab | aa | ab |cc
1 0 0 2 2 1 6 8 0 3 6 11 3 11 4 11 6
| Номер слова | Слово | Номер слова | Слово |
| a | bca | ||
| b | ab | ||
| c | bac | ||
| ba | cca | ||
| aa | abb | ||
| ac | baa | ||
| cc | aba | ||
| cb | aaa | ||
| bc | abc | ||
| ccb |
Сжатый поток состоит из ссылок:
1 0 0 2 2 1 6 8 0 3 6 11 3 11 4 11 6
Входной поток был байтовым, на каждую ссылку отводится тоже один байт, получаем коэффициент сжатия Ксж = 27/17 = 1.588 > 1. Сжатие считается эффективным.
8) aïaaïcïbïcbïbïbbïcïccïbbïbcïaïcc
0 3 2 1 5 1 8 2 10 8 6 0 10
| Номер слова | Слово | Номер слова | Слово |
| a | bb | ||
| b | bbc | ||
| c | cc | ||
| aa | ccb | ||
| aac | bbb | ||
| cb | bca | ||
| bc | ac | ||
| cbb |
Сжатый выходной поток состоит из ссылок: 0 3 2 1 5 1 8 2 10 8 6 0 10.
Входной поток был байтовым, на каждую ссылку отводится тоже один байт, получаем коэффициент сжатия Ксж = 20/13 = 1.538 > 1, следовательно, сжатие считается эффективным.
Сжатие «вручную» 2-х фрагментов данных
c применением кодов Хаффмана
11) gdadafghggfghababahbagggabcdcdcahhggaghhhgacagca
Рассчитаем частоты появления символов алфавита:
g = 13/48 = 0,271
d = 4/48 = 0,083
a = 12/48 = 0,25
f = 2/48 = 0,042
h = 8/48 = 0,167
b = 4/48 = 0,083
c = 5/48 = 0,104
Сформируем дерево:
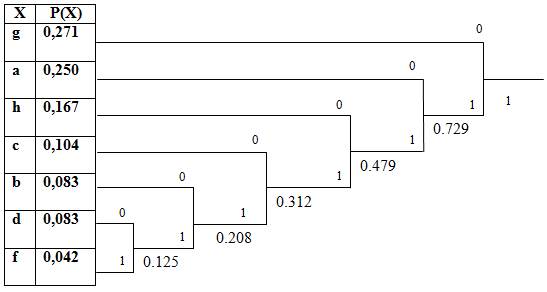
Код Хаффмана символов алфавита:
| X | Code |
| g | |
| a | |
| h | |
| c | |
| b | |
| d | |
| f |
Предположим, что входной поток был байт ориентированным, тогда
Kсж = 8/ (0,271∙1 + 0,250∙2 + 0,167∙3 + 0,104∙4 + 0,083∙5 + 0,083∙6 + 0,042∙6) = 8/ 2,853 = 2,804.
Сжатие считается эффективным.
10) faaadddddbbbccbaffbbbaabbabbbabbfcadcbfababadddab
Рассчитаем частоты появления символов алфавита:
a = 13/49 = 0,265
b = 18/49 = 0,367
c = 4/49 = 0,082
d = 9/49 = 0,184
f = 5/49 = 0,102
Сформируем дерево:

Код Хаффмана символов алфавита:
| X | Code |
| b | |
| a | |
| d | |
| f | |
| c |
Предположим, что входной поток был байт ориентированным, тогда
Kсж = 8/ (0,367∙1 + 0,265∙2 + 0,184∙3 + 0,102∙4 + 0,082∙4) = 8/ 2,185 = 3,661.
Сжатие считается эффективным.
