Системы сравнения с нормой

Существуют два типа систем оценивания относительно нормы; они обеспечивают систему координат, па основе которой кандидатов мож­но сравнить друг с другом. Позиционной называется такая система оценивания, где происходит только классификация кандидатов по от­ношению друг к другу; стандартизированные системы оценок дают информацию как о классификации кандидатов, так и о величине раз­личия между ними. Важно подчеркнуть, что как процентиль, так и результат в рамках стандартизированной системы должны рассмат­риваться но отношению к подходящей эталонной группе. Другими словами, не имеет никакого смысла сравнивать баллы, полученные медсестрами-стажерами, с результатами банковских менеджеров.

Позиционные системы оценки

Наиболее простыми позиционными системами оценки являются те, где результат, полученный кандидатом, оценивается как выше или ниже среднего или же осуществляется ранжирование результатов в порядке убывания, от самых лучших до самых худших. Например, кандидат А по результатам теста А занял третье место, пятое по тесту В и девятое по тесту С. Однако следует помнить, что результаты ран­жирования зависят от количества людей, выполняющих тест, и поло­жение кандидата окажется неодинаковым, если в тестировании при­мут участие меньшее или большее число человек, — это мешает делать обоснованные суждения о том, насколько хорошо люди выполнили задание по сравнению с остальными. Другая сложность состоит в том, что компетентность или другие достоинства кандидатов не отражают­ся на их размещении. Все кандидаты, сдающие тест, могут оказаться более высокого или низкого уровня, чем предыдущие группы.

Позиционные системы оценки ■ 215

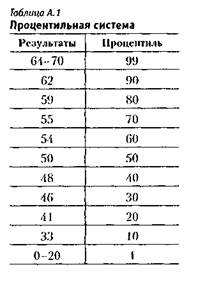
Наиболее сложным типом позиционпой оценки является ироцентиль, т. е. расположение кандидатов в по­рядке репрезентативной очереди,где место каждого определяется по отно­шению к 99 другим (см. табл. А 1). Процентнль показывает, какая доля от остальных кандидатов получили результат ниже, чем те, кто получили определенный процентнльнып ранг. Так, например, если кандидат А полу­чает 75-й процентнль, то это говорит о том, что 75% испытуемых получи­ли более низкие результаты, чем дан­ный кандидат. Причина этого заклю­чается в том, что система основана на процентильных показателях, которые находятся в диапазоне от нуля до ста,при этом самым худшим показателем является нуль, а лучшим — сто. В группе из 100 человек, где все получили разные баллы, тот, чей про-центильный показатель составил 50, будет помещен в очереди на 50-е место, а тот, чей показатель равен 60, — на 60-е. Па практике нор­мальное распределение характеристик людей может приводить к тому, что процентил ьная шкала будет вводить в заблуждение, если ее смысл не до конца понятен. В качестве примера можно представить распре­деление баллов, которые 100 человек получили при выполнении те­ста на вычислительные навыки. Очень немногие люди получат особен­но высокие или крайне низкие результаты; большинство результатов будут сгруппированы вокруг среднего показателя. Десятка лучших ис­пытуемых может получить результаты от, например, 80 до 95 (разни­ца составит 15 пунктов). В середине разброса результатов из-за боль­шой их скученности 50-й процентнль может соответствовать, напри­мер, результатам от 47 до 50 (разница составит 3 пункта). Другими словами, различие, выраженное в форме процентиля, не отражает ре­альной разницы величин полученных баллов. С точки зрения отличий по качеству выполнения заданий расхождения между двумя людьми, помещенными на уровень 90-го и 95-го процентилей, вероятнее всего, окажутся значительно больше, чем между теми, кто находится на 50-м и 55-м процентилях. Все же, даже с учетом этого недостатка, пред-

216 ■ Приложение А. Системы сравнения с нормой

ставлен не результатов в виде процентиля дает два преимущества: кан­дидата возможно сравнить со всеми остальными, выполнившими оп­ределенный тест; кроме того, легко можно оценить данные, получен­ные одним кандидатом при выполнении разных тестов, друг с другом. Основной недостаток состоит в том, что результаты, представленные в форме процентиля, не показывают величину различия между тесто­выми результатами отдельных кандидатов, так как они фиксируют только относительные достижения кандидатов в рамках конкретного тесла.

В случаях, когда требуется более точная и пригодная для интер­претации оценка относительных показателей достижений, становит­ся необходимым учесть не только ранжирование кандидатов, но и ве­личину различия между ними. Именно ото делается с помощью си­стем оценивания, основанных на нормальной кривой, в отношении так называемых стандартных показателей результатов. Из свойств нор­мальной кривой (см. рис. А.1) известно, что одно среднее квадратич­ное отклонение (отрицательное или положительное) охватывает об­ласть, в которой располагаются 68,26% от общего количества резуль­татов теста, два средних квадратичных отклонения соответствуют области расположения 95,44% результатов и 99,74% будут лежать в пределах трех квадратичных отклонений (более подробное рассмот­рение этого вопроса можно найти в работе Миллера, Miller, 1984 tor a fuller discussion). .Зная это свойство нормальной кривой, можно легко выстроить взаимосвязь процентиля и баллов, полученных кандида­тами, и, таким образом, можно получить более удобную для интерпре­тации информацию; делается .это на основе стандартизованного бал­ла (результатов по сравнению со стандартным показателем).

Стандартизованный балл показывает положение балла, получен­ного кандидатом, относительно среднеарифметического балла всех кандидатов, проходивших конкретный тест (т. е. выше или ниже сред­него арифметического), а также то, насколько результат кандидата отличается от среднеарифметического. Эти два свойства стандарти­зованного балла просто отражают две основные характеристики нор­мальной кривой: среднее арифметическое и среднее квадратичное от­клонение. Среднее арифметическое показывает средний результат всех принявших участие в тесте кандидатов, тогда как среднее квадра­тичное отклонение говорит о том, насколько полученный балл отли­чается от среднеарифметического, и становится, таким образом, еди­ницей измерения разброса.

Позиционные системы оценки ■ 217

Самой простой разновидностью стандартизованного балла явля­ется Z-показатель, который указывает только на то, на сколько сред­них квадратичных отклонений результат кандидата выше или ниже среднеарифметического. Кандидат, который получил Z-показатель, равный нулю, находится точно на уровне среднеарифметического по­казателя; гот, у кок) Z-показатель составил минус два (-2) (т. е. отри­цательный балл), -- на два средних квадратичных отклонения ниже среднеарифметического, а кандидат, получивший положительный Z-иоказатель, равный 1,56, находился на 1,56среднего квадратичного отклонения выше среднеарифметического. 11реобразовапне необрабо­танных баллов (rawscores), подученных при помощи теста, в Z-пока­затель осуществляется элементарно просто. Нужно только вычестьпз среднеарифметического балла по тесту «сырой» балл, а затем разде­лить эту разницу на величину размаха (т. е. на среднее квадратичное отклонение). В бол ыпинстве опубликован пых гестов указывается как среднеарифметическое, так и среднее квадратичное отклонение, ос­нованные на норма!тпшых таблицах. Так, например, если среднеариф­метическое для теста составляет 75, а среднее квадратичное отклоне­ние - 15, то у кандидата, получившего на тесте 90 баллов, Z-иоказа­тель будет равен 1,т. е. (90 -75)/15 = 1.

Преимущество применении баллов, основанных на нормальной кривой, для определения различия между кандидатами заключается в том, что каждого из них можно разместить по отношению к осталь­ным, при этом также определяя величину различий между тестовыми результатами. Кроме того, при ;лом не происходит искажения или пре­увеличения различий между кандидатами,так как величина различий в пределах показателей среднего квадратичного отклонения одинако­ва. Следовательно, анализ и интерпретация баллов, полученных по ре­зультатам теста, становится несколько легче.

Как уже было отмечено выше, возможно достаточно эффективное использование взаимосвязи между стандартизованными баллами и процентильными эквивалентами. Стандартизованный балл +1 пока­зывает, что выполнение задания оценивается как одно среднее квад­ратичное отклонение выше среднеарифметического. Как показано на рисунке А.1, известно, что на нормальной кривой определенный процент людей (84,13%) получат стандартизованный балл, состав­ляющий менее +1, а 15,87% получат более высокие результаты. С по­мощью такого способа стандартизованные баллы могут получать интерпретацию непосредственно в форме процентилыюго эквива­лента, и наоборот. Например, для того чтобы оказаться в числе 5%,

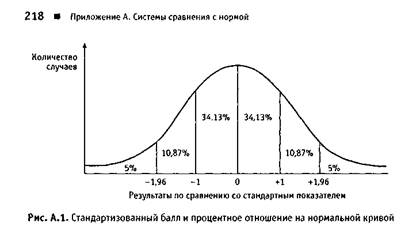
получивших наилучшие результаты, кандидат должен иметь стандар­тизованный балл +1,96. Аналогичным образом стандартизованный балл -1,96 будет указывать на то, что испытуемый относится к 5% вы­полнивших тест хуже всех. Небольшой недостаток стандартизован­ных баллов состоит в том, что форма их представления включает зна­ки «плюс» пли «минус», а также десятичные дроби, при этом знаки после запятой часто теряются при переписывании результатов. Для того чтобы исключить эти проблемы, можно использовать другие виды стандартизованных баллов, полученные путем трансформации Z-иоказателя. Во многих широко распространенных психологических тестах, например в тесте 16PF, часто используются Т-иоказатель (T-score), 10-балльпая шкала пли шкала станов. При переводе в шка­лу станов среднеарифметическому баллу присваивается значение 50, а среднее квадратичное отклонение составляет 10, при атом количе­ство баллов может составлять от 20 до 80. На 10-балльной шкале сред­неарифметическому присваивается значение 5,5, а среднее квадратич­ное отклонение равно 2. Недостатки десятибалльной шкалы состоят в использовании половинных показателей очков, а также в том, что при вычислениях относительно тех, кто получил максимальный ре­зультат, приходится использовать двузначное число. На шкале станов среднеарифметическому присваивается значение 5; шкала станов на­поминает десятибалльную, но при этом стандартизованные баллы могут составлять от 0 до 9. Обе эти разновидности стандартизован­ных баллов не используют показателей ниже 0 и могут непосредствен­но переводиться в форму процентиля.

Приложение Б

Анализ полезности

Подсчет соотношения размеров выгоды и затрат

Для того чтобы создать необходимые условия для обеспечения прибыли, ожидаемой от применения хороших процедур отбора, часто необходимо найти критерий (пли точку отсчета) для сравнения. Обычно эта точка определяется на основе оценки финансовом при­были, которую ожидают получить в том случае, если бы организация-работодатель отбирала людей случайным образом, без учета их уме­ний, навыков пли способностей.

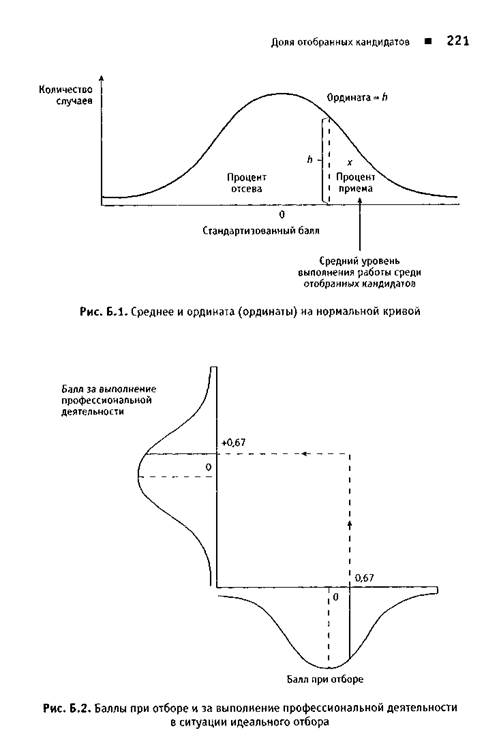
Если бы отбор персонала осуществлялся совершенно случайным образом, то принималось бы большое число людей со средними по­казателями качества их работы, при этом большинство из них оказа­лось бы посередине при ранговой оценке. Показатели качества рабо­ты небольшого числа людей будут располагаться от отметки «ниже среднего» и до очень неудовлетворительного уровня. Такое же не­большое число людей покажет результаты до некоторой степени выше средних. Другими словами, как видно на рис. Б.1, показатели баллов за выполнение работы получили бы нормальное распределение ко-локолообразной формы, имеющее три особенно важных характери­стики:

• центральную точку кривой, соответствующую среднему баллу {среднеарифметическое);

• среднее квадратичное отклонение (5D), представляющее разброс баллов от среднеарифметического;

• ординату, представляющую высоту кривой в любой данной точке нижней оси.

220 ■ Приложение Б. Анализ полезности

Доля отобранных кандидатов

Хорошим отбор кадров определяется наличием числа кандидатов, превышающего число вакансии. Действительно, если бы не было воз­можности произвести отбор из группы имеющихся кандидатов, то баллы кандидатов за выполнение работы имели бы такое же распре­деление, как и в случае отбора сотрудников случайным образом.

Однако в случае, когда имеется возможность отобрать пз каждых четырех кандидатов одного, т. е. кандидатов в четыре раза больше, чем предлагаемых рабочих мест, можно предположит!), что принятие ре­шений но отбору персонала принесет некоторую прибыль. Другими словами, в ситуации идеального отбора доля отобранных кандидатов (т. е. отношение числа должностей к числу кандидатов) составляет около 0,25. В атом случае становится возможным отобрать 25% самых лучших с точки зрения балла при отборе кандидатов, и они также бу­дут темп 25% сотрудников, кто выполняет работу на самом высоком уровне (рис. Б.2).

Следовательно, при оценке финансовом прибыли от отбора персо­нала в первую очередь следует учесть долю отобранных кандидатов. If ел и же необходимо принять всех кандидатов (т. е. доля отобранных равна единице), то получить прибыль от отбора невозможно. Следо­вательно, чем большее имеется число кандидатов и чем меньше число вакансий, тем меньше будет доля отобранных кандидатов и тем боль­шую потенциальную прибыль сможет получить организация благо­даря отбору небольшой группы хороших кандидатов из большего чи­сла претендентов. Таким образом, по сути, доля отобранных кандида­тов отражает достоинства, пли качество, принимаемых кандидатов, и она может использоваться для установления минимально допусти­мого уровня показателей, разграничивающего принимаемых и отсеи­ваемых кандидатов.

Аналогичным образом доля отобранных кандидатов может исполь­зоваться для того, чтобы оценить средний уровень будущей работы принимаемых кандидатов. (Перед тем как начать разбираться с основ­ными идеями, изложенными в следующих абзацах, читателю следует обязательно обратиться к той части приложения А, где речь идет об определении «стандартизованных баллов».) Если бы возможно было безошибочно определить 25% лучших кандидатов (т. е. если бы про­цедура отбора была абсолютно совершенна), то те же самые люди выполняли бы работу на аналогичном уровне. Для любой группы

222 ■ Приложение В. Анализ полезности

нормально распределенных баллов можно подсчитать средний балл. Для этого соответствующий стандартизованный балл (см. приложе­ние Л) следует разделить на высоту (ординату) той части нормальной кривой, где располагается стандартизованный балл. 11а основе стати­стических таблиц можно определить, насколько производительность труда 25% лучших кандидатов будет выше, чем у остальных; для это­го следует найти соответствующий стандартизованный балл и орди­нату. Например, если доля отобранных кандидатов равна 0,25, то их баллы будут расположены на 0,67 среднего квадратичного отклоне­ния выше среднеарифметического, а соответствующая этой точке ор­дината при нормальном распределении составляет 0,319. Если затем ординату разделить на долю отобранных кандидатов, то полученный результат будет указывать па средний уровень выполнения профес­сиональной деятельности темп, чьи результаты располагаются в соот­ветствующем диапазоне; этот уровень, стандартизованный балл за выполнение профессиональной деятельности {standardizedperformance score), обозначается как Z_x. (В рамках целен нашей книги вывод мате­матического выражения для этого этапа мы решили не рассматри­вать.) В случае идеально проведенного отбора доля отобранных канди­датов, равная 0,25, говорит о том, что средние показатели выполнения задания отобранными кандидатами на 1,28 среднего квадратичного отклонения выше среднего (т. е. 0,319/0,33).