Разделение канального ресурса во времени

4.1. Обслуживание пуассоновских потоков

Длительность занятия канального ресурса на передачу информации, относящейся к одному соединению, определяется статистическими свойствами источника трафика и используемой дисциплиной распределения свободного ресурса.

Существует две модели занятия канального ресурса: статическая и динамическая. В статической модели продолжительность случайного времени занятия ресурса определяется выбранной функцией распределения и не зависит от процесса передачи информации в данном соединении и от степени загрузки рассматриваемого сегмента сети. В динамической модели, напротив, длительность времени занятия канального ресурса увеличивается или уменьшается в зависимости от уровня загрузки сети и определяется используемыми механизмами контроля QoS. Динамический режим может, например, осуществляться введением приоритетов обслуживания для заявок различного типа, когда канальный ресурс предоставляется заявками более высоких приоритетов, а низкоприоритетные заявки ожидают своей очереди.

В дальнейшем, более детально мы рассмотрим модели, характеризующие поступление пакетного трафика от различного типа услуг, на уровне доступа [1].

Допустим, что оператор выделяет некоторому коллективному абоненту, для оказания K различных типов услуг (k=1…K), канальный ресурс, с пропускной способностью С [бит/с]. По каждому k-му типу услуги у абонента имеется N_k пользователей. Средняя интенсивность поступления пакетов от пользователя k-й услуги составляет l_pk пакетов в секунду. Тогда, средняя суммарная интенсивность поступления пакетов от всех пользователей услуги k может быть представлена формулой (4.1).

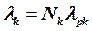(4.1)

Допустим, что каждая услуга, типа k, реализуется посредством передачи пакетов, имеющих битовую длину L_k (включая минимальный межпакетный интервал). Тогда, длительность передачи одного пакета k -го типа примет вид (4.2), а коэффициент загрузки канального ресурса передачей пакетов услуги k -го типа – вид (4.3).

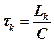	(4.2)
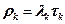	(4.3)

Параметр r_k показывает вероятность того, что канал занят передачей пакетов услуги k -го типа, т.е. долю канального ресурса, занимаемую передачей пакетов, относящихся к указанной услуге.

Суммарную долю канального ресурса, занятую передачей всех пакетов, выразим как (4.4).

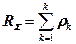(4.4)

Устойчивая передача всех пакетов без потерь возможна лишь при условии R_S £ 1.

С учетом улучшения показателей качества обслуживания QoS, пакетам различных услуг присваиваются различные приоритеты передачи. Пакетам услуг, чувствительным к задержкам по времени, присваиваются более высокие приоритеты.

Таким образом, рассматриваемая модель предлагает разделение во времени всего канального ресурса между отдельными пользователями. Каждому пакету услуги k -го типа отводится для передачи канальный ресурс, в виде интервала времени t_k, причем, интервалы не пересекаются.

Из теории вероятностей известно, что при суммировании большого числа независимых потоков заявок с малыми интенсивностями и постоянной суммарной интенсивностью, свойства результирующего потока будут приближаться к пуассоновскому закону.

Будем считать, что для рассматриваемого сегмента мультисервисной сети выполняются предположения о возможности использования пуассоновской модели входного потока заявок с интенсивностью поступления и потребностями в канальном ресурсе, зависящими от номера потока. Данное предложение можно считать справедливым в транзитной части сети, где происходит смешивания большого числа потоков заявок.

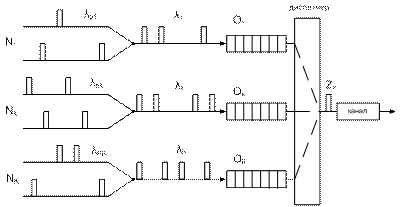Рис. 4.1

На рис. 4.1 представлена организация обработки заявок с относительными приоритетами в одноканальной системе с разделением ресурса во времени. Относительность приоритета связана с тем, что никакая заявка более высокого приоритета не может прервать передачу заявки (пакета), уже находящейся на обслуживании в канале. Любая заявка, захватившая канал передачи имеет на это время самый высокий приоритет.

Заявки каждого из приоритетов выстраивается в соответствующие очереди O₁…O_k…O_K.

Программа «диспетчер» выбирает заявку из очереди, имеющей на данный момент наивысшей приоритет. Если в систему поступают k приоритетные простейшие потоки (k=1…K) с интенсивностями l₁…l_K, длительности передачи пакетов каждого потока имеют математические ожидания 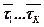и вторые начальные моменты 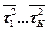, соответственно, то среднее время ожидания пакетов заявок, имеющих приоритеты 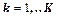, определяется соотношением (4.5).

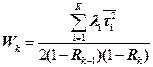,	(4.5)
где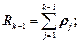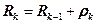

Среднее количество пакетов k-го приоритета, ожидающих в очереди (4.6)

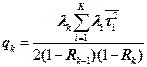(4.6)

При бесприоритетном обслуживании К потоков с различными математическими ожиданиями 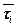и вторыми начальными моментами 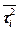времени обслуживания, число заявок k-го потока в очереди определяется соотношением (4.7).

,

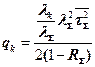(4.7)

где

,

,

.

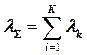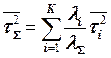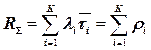l_k/l_S - представляет вероятность заявки k-го типа в суммарном потоке заявок. Суммарное число заявок всех типов q_S, находящихся в очереди .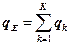

И, наконец, если рассматриваются однопоточные системы, с заданным законом распределения времен обслуживания, то справедливо соотношение (4.8).

,

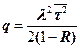(4.8)

где

l=lS ,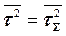

,

R=RS..

Формула (4.8) называется формулой Хинчина–Поллячека, носит в теории очередей фундаментальный характер и широко используется при расчете систем массового обслуживания с очередями.

В таблице 4.1 показаны основные соотношения, определяющие средние значение задержек и очередей для различных систем массового обслуживания.

Напомним, что перечисленные результаты получены при условии, что все потоки являются пуассоновскими, в этом случае и результирующий поток также является пуассоновским. Пуассоновская модель обычно относится к потоку первичных заявок, получаемому от многих однородных источников одновременно.

Таблица 5.

Формулы для распределения математических ожиданий
Время обслуживания в очереди	Размер очереди
Обслуживание К потоков с относительными приоритетами и случайными временами обслуживания
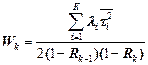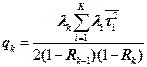Бесприоритетное обслуживание К потоков со случайными временами обслуживания
;
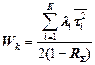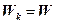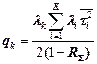Обслуживание бесприоритетное К потоков с различными постоянными временами об служивания
;
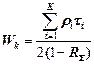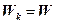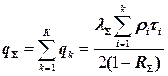Обслуживание бесприоритетное К потоков с одинаковыми случайными временами обслуживания
;
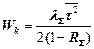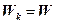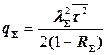Обслуживание одного потока интенсивности l и случайным временем
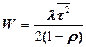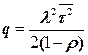