Оценка надежности программ по числу прогонов (модель Нельсона)
В такой модели за показатель надежности программы принимается вероятность 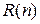 безотказного выполнения n прогонов программы.
безотказного выполнения n прогонов программы.
Вероятность того, что j–й прогон закончится отказом,
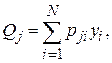 (2.6)
(2.6)
где 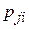 – вероятность выбора i-ого набора входных данных при j–м прогоне некоторой последовательности прогонов;
– вероятность выбора i-ого набора входных данных при j–м прогоне некоторой последовательности прогонов; 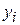 – «динамическая переменная», принимающая значение 0, если прогон программы при i–м наборе входных данных оказывается успешным, и значение 1, если этот прогон заканчивается отказом; N – число возможных наборов входных данных.
– «динамическая переменная», принимающая значение 0, если прогон программы при i–м наборе входных данных оказывается успешным, и значение 1, если этот прогон заканчивается отказом; N – число возможных наборов входных данных.
На практике надежность программы может быть оценена путем прогона программы на n наборах входных данных и вычисления значения оценки
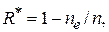
где 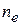 – число наборов входных данных, при которых произошли отказы.
– число наборов входных данных, при которых произошли отказы.
Для получения 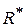 вначале находят «функциональный разрез» программы, т. е. множество вероятностей
вначале находят «функциональный разрез» программы, т. е. множество вероятностей 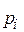 того, что будет сделан выбор i–ого варианта входных данных. Для этого разбивают все пространство входных переменных на подпространства и находят вероятности того, что выбранный набор входных данных будет принадлежать конкретному подпространству. Это можно сделать, оценивая вероятности появления различных входов в реальных условиях функционирования, для которых оценивается надежность программы.
того, что будет сделан выбор i–ого варианта входных данных. Для этого разбивают все пространство входных переменных на подпространства и находят вероятности того, что выбранный набор входных данных будет принадлежать конкретному подпространству. Это можно сделать, оценивая вероятности появления различных входов в реальных условиях функционирования, для которых оценивается надежность программы.
Далее формируют случайную выборку из n наборов входных данных, распределенных в соответствии с 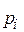 (например, с помощью датчика случайных чисел), и проводят n прогонов программы, находят
(например, с помощью датчика случайных чисел), и проводят n прогонов программы, находят 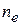 и вычисляют
и вычисляют 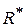 .
.
Чтобы установить связь между моделями по наработке и по прогонам, запишем
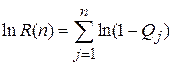 (2.7)
(2.7)
или
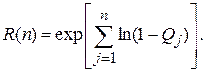 (2.8)
(2.8)
Обозначим 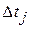 время выполнения j-ого прогона программы
время выполнения j-ого прогона программы
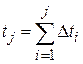 – суммарное время выполнения первых j прогонов программы и примем, что
– суммарное время выполнения первых j прогонов программы и примем, что
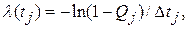 (2.9)
(2.9)
при этом
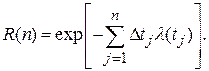 (2.10)
(2.10)
При 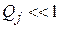 функция
функция 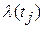 может рассматриваться как функция интенсивности отказов.
может рассматриваться как функция интенсивности отказов.
Оценка надежности программ на ранних стадиях проектирования.Описанные выше модели надежности программ требуют оценки ряда параметров по статистическим данным, получаемым при тестировании, отладке программ или на этапе передачи программ в эксплуатацию. На ранних этапах проектирования программ отсутствует возможность проведения экспериментов, могут быть использованы статистические данные об отказах аналогичных программ, созданных ранее той же группой программистов. Рядом исследователей выявлена стабильность относительной частоты ошибок в различных типовых конструкциях алгоритмических языков высокого уровня. Рассмотрим модель надежности программы, основанную на этом явлении и учитывающую структуру программы и распределение исходных данных.
В этой модели предполагается, что:
а) исходные данные выбираются случайно в соответствии имеющимся распределением их вероятностей;
б) ошибки в элементах программы независимы;
в) программа образована из элементов немногих s классов с одинаковыми вероятностями pl правильного однократного исполнения элементов класса l.
При этих допущениях условная вероятность pi правильного однократного пути исполнения программы при условии исполнения пути i
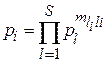 , (2.11)
, (2.11)
где mli – количество элементов l – ого класса в i-ом пути (путь – последовательность элементов программы, не содержащая ответвлений и используемая при выполнении программы с определенными исходными данными).
Вероятность правильного однократного исполнения всей программы
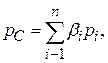 (2.12)
(2.12)
где 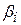 – вероятность выбора i-ого пути (зависит от сочетания значений исходных данных).
– вероятность выбора i-ого пути (зависит от сочетания значений исходных данных).
Если программа в процессе эксплуатации не корректируется, т. е. проявившиеся ошибки не устраняются, вероятности pi неизменны. При корректировании программ вероятность правильного однократного исполнения элемента l-го класса в период между (j-1)-й и j-й ошибками
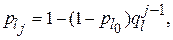 (2.13)
(2.13)
где 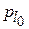 – вероятность правильного однократного исполнения элемента l-го класса до начала эксплуатации или отладки программы; ql – параметр эффективности корректировки (показывает, во сколько раз изменяется вероятность появления ошибки в элементе l–ого класса после ее устранения).
– вероятность правильного однократного исполнения элемента l-го класса до начала эксплуатации или отладки программы; ql – параметр эффективности корректировки (показывает, во сколько раз изменяется вероятность появления ошибки в элементе l–ого класса после ее устранения).
При одинаковых ql = q вероятность правильного однократного исполнения всей программы между (j-1)и j–м отказами
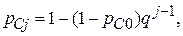 (2.14)
(2.14)
где pC0 – вероятность правильного однократного исполнения программы до начала ее эксплуатации или отладки.
Если программа не корректируется после обнаружения в ней ошибок, q=1. Если корректировки неудачны, например, из-за плохого знания программы, q>1. При 0<q<1 корректировки повышают надежность программы.
Если элементами программы являются операторы алгоритмического языка высокого уровня, целесообразно объединить операторы в следующие группы:
1) элементы ввода-вывода (включая операторы формата);
2) элементы цикла: операторы цикла, в том числе и операторы условного перехода, с помощью которых организуется цикл;
3) логические элементы: операторы условного и безусловного переходов;
4) исполняемые элементы: вычислительные операторы, операторы присваивания, вызова подпрограмм;
5) неисполняемые элементы: операторы задания режимов, распределения памяти, закрепления устройств и т. д.
Для приближенной оценки выделяется всего два класса, в один из которых входят элементы групп 2 и 3, в другой – групп 1, 4, 5.
На практике наиболее часто используемые пути программы отлаживаются очень тщательно, вплоть до полного исключения возможных ошибок (полной отлаженности пути). Эту особенность можно учесть, предположив, что программа передается в эксплуатацию после полной отлаженности всех путей, вероятность выбора которых превышает 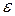 . Учтя зависимость проявления отказа в элементе программы от исходных данных, имеем
. Учтя зависимость проявления отказа в элементе программы от исходных данных, имеем

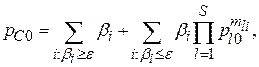 (2.15)
(2.15)
где первая сумма находится по всем путям с номерами i, для которых вероятность выбора 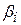 превышает
превышает 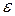 , вторая – по маловероятным путям, вероятность выбора которых меньше
, вторая – по маловероятным путям, вероятность выбора которых меньше 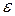 .
.
Оценки pC0 и q по экспериментальным данным находятся по числу 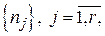 прогонов программы до обнаружения отказа. При этом максимально правдоподобные оценки получаются в результате решения системы уравнений:
прогонов программы до обнаружения отказа. При этом максимально правдоподобные оценки получаются в результате решения системы уравнений:
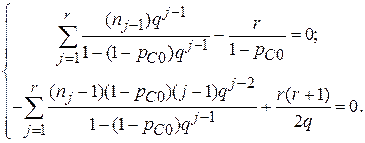 (2.16)
(2.16)
