Двумя точками ( а и в )

Через эти точки можно провести прямую линию получим отрезок [BA]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка:

[A1B1] < [BA]; [A2B2] < [BA]; [A3B3] < [BA].

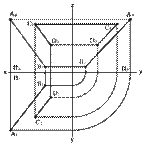
2. Двумя проекциями. Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [А1В1] и [A2B2]. Проведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные, линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А1В1] и
[А2В2].

Рис. 18. Задание прямой двумя проекциями

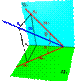
3. Точкой и углами наклона к плоскостям проекций.

Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве.

Геометрические образы, заданные неподвижными объектами, создают статичные геометрические образы. Статичные геометрические образы рассматриваются при создании неподвижных объектов: проектировании зданий, промышленных сооружений.

Рис. 19. Задание прямой точкой и углами

Кинематически прямая задаётся одной точкой и единственным направлением движения. Если при перемещении точка меняет направление движения, то формируется либо ломаная, состоящая из отрезков, либо кривая линия.

Кинематическую линию в быту называют траекторией. В свою очередь, линии (траектории) бывают плоскими, если некоторая точка (букашка) перемещается по плоскости, и пространственными, если некоторая точка (букашка) перемещается (летает) в пространстве, меняя направление перемещения в трёхмерном пространстве.

Рис. 20. Виды траекторий

Плоскость – одно из основных понятий геометрии.

Рис. 21. Плоскость

Некоторые характеристические свойства плоскости:

1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;

2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.

Плоскость в линейной алгебре - поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением 1-ой степени. Общее уравнение плоскости:

Ax+By+Cz+D=0,

где А, В, С, и D - постоянные, причем А, В и С одновременно не равны нулю.

Положение плоскости в пространстве можно определить:

1.

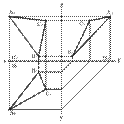Тремя точками, не лежащими на одной прямой линии

Рис. 22

2. Прямой линией и точкой, не принадлежащей этой прямой

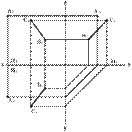Рис. 23

3.

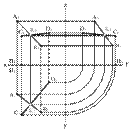Двумя пересекающимися прямыми

Рис. 24

4.

Двумя параллельными прямыми

Рис. 25

Поверхность - двумерный геометрический образ (можно измерить площадь данного рассматриваемого объекта), представляет непрерывное множество точек, расположение которых подчинено определённому закону, определяемому алгоритмом формирования задаваемого геометрического образа.

Рис. 26. Поверхность

Как и линии, поверхности могут быть представлены статично и кинематически.

На чертежах поверхности обозначают прописными буквами греческого алфавита: Α, Β, Γ, Δ, Ε, Ζ,…, а строчными буквами греческого алфавита: α, β, γ, δ, ε,ζ,..., - обозначают углы.

Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z) - многочлен n-ой степени) и трансцендентные (F(x,y,z) - трансцендентная функция).

Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. То есть, произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность.

В начертательной геометрии фигуры задаются графически, поэтому целесообразно поверхность рассматривать как совокупность всех последовательных положений некоторой перемещающейся в пространстве линии.

Рис. 27

Поверхность можно рассматривать, как совокупность последовательных положений l₁,l₂… линии l, перемещающейся в пространстве по определенному закону. В процессе образования поверхности линия l может оставаться неизменной или менять свою форму - изгибаться или деформироваться.

Подвижную линию принято называть образующей, неподвижные - направляющими. Такой способ образования поверхности принято называть кинематическим.

По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая.

Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся.

Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Это так называемые циклические поверхности

Рис. 28

Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности.

Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом.

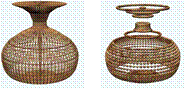а) б)

Рис. 29. а) каркас, б) точечный каркас

Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.

Различают две части определителя: геометрическую и алгоритмическую.

Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.

Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.

ПОВЕРХНОСТИ ВРАЩЕНИЯ

Поверхности вращения – это поверхности созданные при вращении образующей mвокруг оси i.

Геометрическая часть определителя состоит из двух линий: образующей m и оси i.

Алгоритмическая часть включает две операции:

1. На образующей mвыделяют ряд точек A, B, C,…F;

2. Каждую точку вращают вокруг оси i.

Рис. 30

Так создается каркас поверхности, состоящей из множества окружностей, плоскости которых расположены перпендикулярно оси i.

Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором.

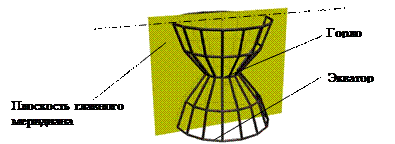Рис. 31

Из закона образования поверхности вращения вытекают два основных свойства:

1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.

2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам.

Плоскость проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана.

Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими.

Сфера – образуется вращением окружности вокруг её диаметра.

При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг большой оси то эллипсоид называется вытянутым, если вокруг малой – сжатым или сфероидом.

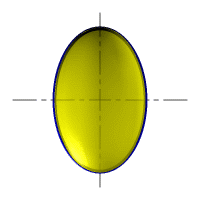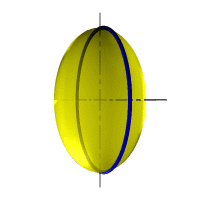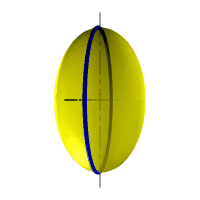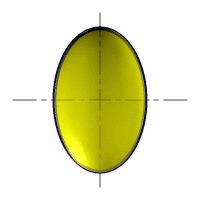
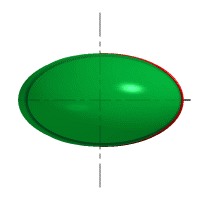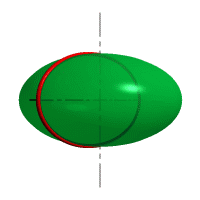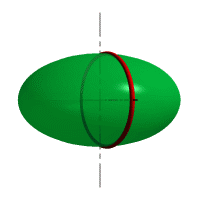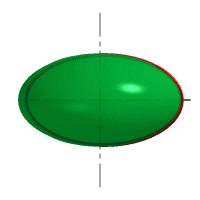
Рис. 32. Сфера, вытянутый эллипсоид, сжатый эллипсоид

Тор– поверхность тора формируется при вращении окружности вокруг оси, не проходящей через центр окружности.

Параболоид вращения– образуется при вращении параболы вокруг своей оси.

Гиперболоид вращения– различают одно и двух полостной гиперболоиды вращения.

Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.

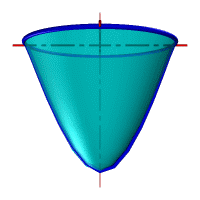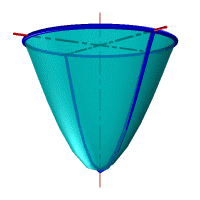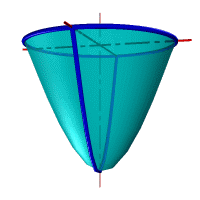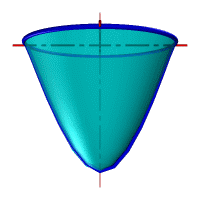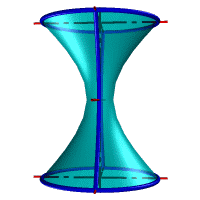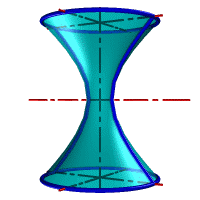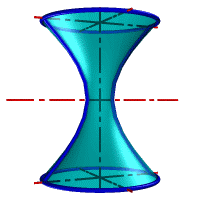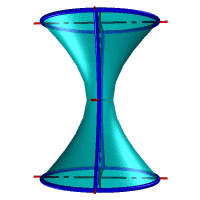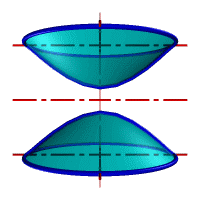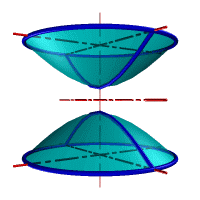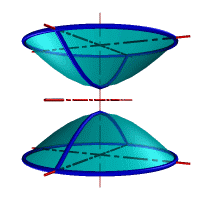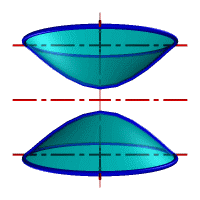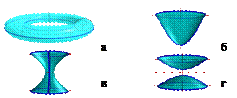Рис.33. а) тор, б) параболоид, в) однополостной гиперболоид, г) двухполостной гиперболоид

ВИНТОВЫЕ ПОВЕРХНОСТИ

Винтовые поверхности образуются винтовым движением некоторой линии – образующей.

Под винтовым движением понимается совокупность двух движений: поступательного параллельно некоторой оси, и вращательного, вокруг той же оси.

Рис. 34. Винтовая поверхность

При этом поступательное и угловое перемещение находятся в определенной зависимости

∆h=k∆v,

где ∆h – линейное перемещение за время ∆t, ∆v– угловое перемещение за то же время, k – коэффициент пропорциональности.

Если k=Const, то шаг поверхности постоянный.

Геометрическая часть определителя винтовой поверхности ни чем не отличается от поверхности вращения и состоит из двух линий: образующей m, и оси i(рис.35).

А

С

В

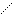
Рис. 35

Алгоритмическая часть:

1. На образующей m выделяют ряд точек А, В, С, …

2. Строят винтовые линии заданного шага и направления, по которым перемещаются заданные точки.

ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА (ПОВЕРХНОСТИ КАТАЛАНА)

Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих), параллельных некоторой плоскости α (плоскости параллелизма) и пересекающих две данные направляющие m, n.

В зависимости от формы направляющих образуются три частных вида поверхностей.

Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих), параллельных некоторой плоскости α (плоскости параллелизма) и пересекающих две данные направляющие m, n.

В зависимости от формы направляющих образуются три частных вида поверхностей.

Цилиндроид. Цилиндроидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим кривым линиям, при этом образующая во всех положениях параллельна плоскости параллелизма (см. рис.36).

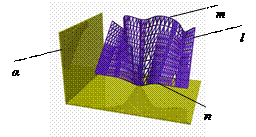
Рис. 36

Коноид. Коноидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим, одна из которых кривая линия, а другая прямая, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.37).

Рис.37

Гиперболический параболоид.Гиперболическим параболоидом или косой плоскостью называется поверхность, образованная движением прямолинейной образующей, параллельной плоскости параллелизма, по двум направляющим линиям – скрещивающимся прямым (рис. 38).

Рис.38