Простейшие алгоритмы направленного случайного поиска
Алгоритм парной пробы.В данном алгоритме четко разделены пробный и рабочий шаги.
Пусть  – найденное на
– найденное на 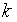 -м шаге наименьшее значение минимизируемой функции
-м шаге наименьшее значение минимизируемой функции 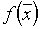 . По равномерному закону генерируется случайный единичный вектор
. По равномерному закону генерируется случайный единичный вектор  и по обе стороны от исходной точки
и по обе стороны от исходной точки  делаются две пробы: проводим вычисление функции в точках
делаются две пробы: проводим вычисление функции в точках 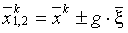 , где
, где  -величина пробного шага.
-величина пробного шага.
Рабочий шаг делается в направлении наименьшего значения целевой функции. Очередное приближение определяется соотношением
 .
.
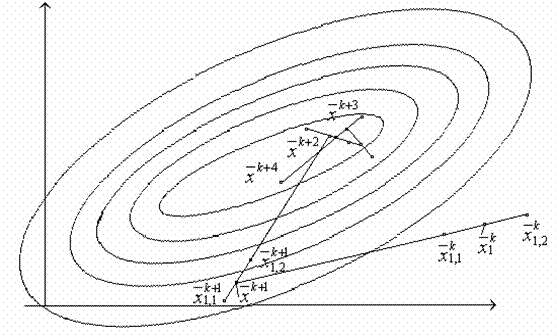
Рис.
Особенностью данного алгоритма является его повышенная тенденция к “блужданию”. Даже найдя экстремум, алгоритм может увести процесс поиска в сторону.
Алгоритм наилучшей пробы. На 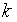 -м шаге мы имеем точку
-м шаге мы имеем точку  . Генерируется
. Генерируется 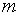 случайных единичных векторов
случайных единичных векторов  . Делаются пробные шаги в направлениях
. Делаются пробные шаги в направлениях 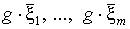 и в точках
и в точках 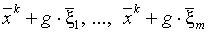 вычисляются значения функции. Выбирается тот шаг, который приводит к наибольшему уменьшению функции:
вычисляются значения функции. Выбирается тот шаг, который приводит к наибольшему уменьшению функции: 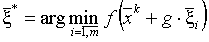 . И в данном направлении делается шаг
. И в данном направлении делается шаг
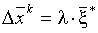 .
.
Параметр  может определяться как результат минимизации по направлению, определяемому наилучшей пробой, или выбираться по определенному закону.
может определяться как результат минимизации по направлению, определяемому наилучшей пробой, или выбираться по определенному закону.
С увеличением числа проб выбранное направление приближается к направлению  .
.
Если функция  близка к линейной, то есть возможность ускорить поиск, выбирая вместе с наилучшей и наихудшую пробу. Тогда рабочий шаг можно делать или в направлении наилучшей, или в направлении, противоположном наихудшей пробе.
близка к линейной, то есть возможность ускорить поиск, выбирая вместе с наилучшей и наихудшую пробу. Тогда рабочий шаг можно делать или в направлении наилучшей, или в направлении, противоположном наихудшей пробе.
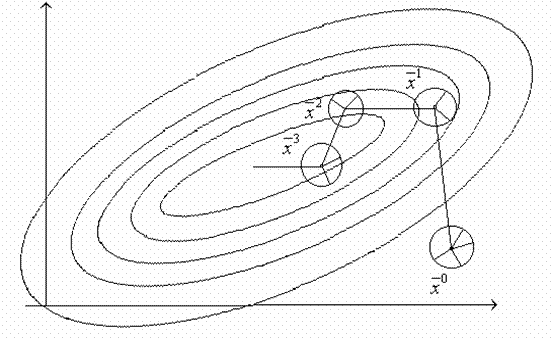
Рис.
Метод статистического градиента.Из исходного состояния  делается
делается 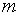 независимых проб
независимых проб  в
в 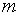 случайных направлениях, а затем вычисляются соответствующие значения минимизируемой функции в этих точках. Для каждой пробы запоминаем приращения функции
случайных направлениях, а затем вычисляются соответствующие значения минимизируемой функции в этих точках. Для каждой пробы запоминаем приращения функции
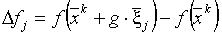 .
.
После этого формируем векторную сумму
 .
.
В пределе при 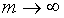 направление
направление  совпадает с направлением градиента целевой функции. При конечном
совпадает с направлением градиента целевой функции. При конечном 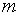 вектор
вектор  представляет собой статистическую оценку направления градиента. В направлении
представляет собой статистическую оценку направления градиента. В направлении  делается рабочий шаг и, в результате, очередное приближение определяется соотношением
делается рабочий шаг и, в результате, очередное приближение определяется соотношением
 .
.
При выборе оптимального значения  , которое минимизирует функцию в заданном направлении, мы получаем статистический вариант метода наискорейшего спуска. Существенное преимущество перед детерминированными алгоритмами заключается в возможности принятия решения о направлении рабочего шага при
, которое минимизирует функцию в заданном направлении, мы получаем статистический вариант метода наискорейшего спуска. Существенное преимущество перед детерминированными алгоритмами заключается в возможности принятия решения о направлении рабочего шага при  . При
. При 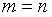 и неслучайных ортогональных рабочих шагах, направленных вдоль осей координат, алгоритм вырождается в градиентный метод.
и неслучайных ортогональных рабочих шагах, направленных вдоль осей координат, алгоритм вырождается в градиентный метод.

Рис.
Алгоритм наилучшей пробы с направляющим гиперквадратом. Внутри допустимой области строится гиперквадрат. В этом гиперквадрате случайным образом разбрасывается 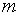 точек
точек  , в которых вычисляются значения функции. Среди построенных точек выбираем наилучшую. Таким образом, на 1-м этапе координаты случайных точек удовлетворяют неравенствам
, в которых вычисляются значения функции. Среди построенных точек выбираем наилучшую. Таким образом, на 1-м этапе координаты случайных точек удовлетворяют неравенствам  , и
, и  – точка с минимальным значением целевой функции.
– точка с минимальным значением целевой функции.
Опираясь на эту точку, строим новый гиперквадрат. Точка, в которой достигается минимум функции на 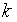 -м этапе, берется в качестве центра нового гиперквадрата на
-м этапе, берется в качестве центра нового гиперквадрата на  -м этапе.
-м этапе.
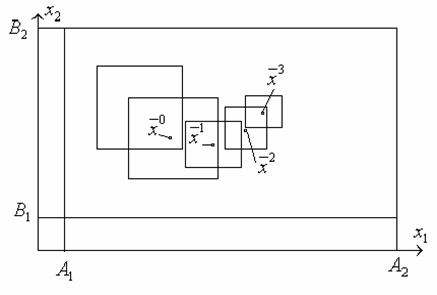
Рис.
Координаты вершин гиперквадрата на  -м этапе определяются соотношениями
-м этапе определяются соотношениями
 ,
,  ,
,
где 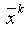 – наилучшая точка в гиперквадрате на
– наилучшая точка в гиперквадрате на 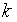 -м этапе.
-м этапе.
В новом гиперквадрате выполняем ту же последовательность действий, случайным образом разбрасывая 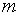 точек. В результате осуществляется направленное перемещение гиперквадрата в сторону уменьшения функции.
точек. В результате осуществляется направленное перемещение гиперквадрата в сторону уменьшения функции.
В алгоритме с обучением стороны гиперквадрата могут регулироваться в соответствии с изменением по некоторому правилу параметра  , определяющего стратегию изменения стороны гиперквадрата. В этом случае координаты вершин гиперквадрата на
, определяющего стратегию изменения стороны гиперквадрата. В этом случае координаты вершин гиперквадрата на  -м этапе будут определяться соотношениями
-м этапе будут определяться соотношениями
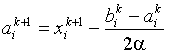 ,
,  .
.
Хорошо выбранное правило регулирования стороны гиперквадрата приводит к достаточно эффективному алгоритму поиска.
В алгоритмах случайного поиска вместо направляющего гиперквадрата могут использоваться направляющие гиперсферы, направляющие гиперконусы.
