Оценка канального ресурса на уровне установления соединения

При анализе трафика на уровне установления соединений основное внимание должно уделяться оценке канального ресурса, необходимого для успешного пропуска потоков заявок различного типа. Если при поступлении заявки, канального ресурса, необходимого для ее обслуживания недостаточно, то такая заявка теряется.

Требуемый канальный ресурс может быть охарактеризован требуемой пропускной способностью С [кбит/с].

Единица требуемого канального ресурса (канальная единица – ке) характеризуется пропускной способностью С₀ [кбит/с/ке]. За С₀ может быть принята пропускная способность канала, необходимая для передачи голосовых сообщений (например, 64 кбит/с/ке).

Пропускная способность i, выраженная в числе канальных единиц определяется как .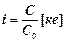

В модели [1] имеется n потоков заявок на выделение канального ресурса, необходимого для обслуживания трафика сервисов реального времени (речевые сообщения, видеоконференц–связь и т.д.). Поступление заявок k-го потока подчиняется закону Пуассона с интенсивностью λ_k, где k=1,2,..,n.

Пусть ϑ- пропускная способность имеющейся линии, выраженная в числе канальных единиц, b_k- пропускная способность требуемая для обслуживания одной заявки потока k, выраженная в канальных единицах.

i_k- число заявок k-го потока, находящихся в системе.

Число канальных единиц, занятых на обслуживание всех заявок, находящихся в системе обозначим через (7.1)

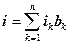(7.1)

Если в систему поступит еще одна дополнительная заявка потока k, требующая для своего обслуживания b_k канальных единиц, то при обслуживании очередей заявок она примется к обслуживанию, если выполняется неравенство (7.2)

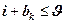(7.2)

В противном случаи она безвозвратно отвергается.

Пусть i_k(t) - число заявок k -го потока, находящихся в момент времени 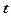на обслуживании. Динамика изменения общего числа обслуживаемых заявок описывается многомерным случайным процессом r(t)=(i₁(t),i₂(t),…,i_n(t)), определенным на конечном пространстве состояний S. Оно состоит из векторов (i_1,,i₂,…,i_n), удовлетворяющих неравенству(7.3)

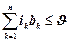(7.3)

Обозначим через ρ(i_1,,i₂,…,i_n) стационарную вероятность состояния (i_1,,i₂,…,i_n), где i_k - число заявок k-го потока, находящихся на обслуживании в стационарном режиме k=1,2,..,n.

Качество обслуживания заявок k-го потока определяется долей π_k потерянных заявок и средней величиной m_k занятого канального ресурса. Дадим им формальные определения с использованием вероятностей ρ(i_1,,i₂,…,i_n). Доля потерянных заявок k-го потока находится как доля времени пребывания процесса r(t) в состояниях, когда прием поступившей заявки невозможен из-за нехватки свободного канального ресурса.

Обозначим через U_k множество соответствующих состояний. Она включает в себя состояния (i_1,,i₂,…,i_n)єS, удовлетворяющие условию(7.4)

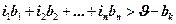(7.4)

Значения введенных показателей обслуживания заявок k-го потока определяются из равенств(7.5), (7.6)

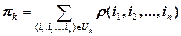	(7.5)
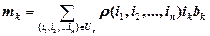	(7.6)

Если все потоки заявок простейшие, то заявки каждого из потоков обслуживаются независимо, и для совместных вероятностей получим следующее выражение

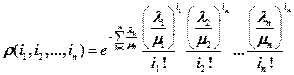(7.7)

Из него следует, что

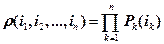(7.8)

i=0,1,...; k=1…n , где

,

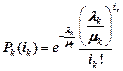(7.9)

λ_k- средняя интенсивность поступления заявок k-го типа

μ_k- средняя интенсивность обслуживания этих заявок

Очевидно, что

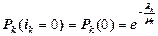(7.10)

Отношение (7.9) включает коэффициент загрузки канала заявками k-го типа.

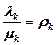(7.11)

Подставляя в (7.8), получим

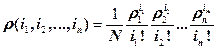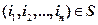,	(7.12)
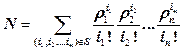.	(7.13)

Полученные выражения можно использовать для оценки π_k, m_k

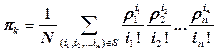	(7.14)
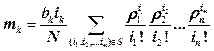	(7.15)

Здесь π_k- доля потерянных заявок k-го потока, а m_k- среднее число каналов, занимаемых заявками.

Параметры π_k и m_k- характеризуют качество обслуживания заявок k -го типа при наличии отказов, из-за нехватки канального ресурса.

Заявки не становятся в очередь, а сразу же покидают в систему и теряются. (Телефонные вызовы, при сигнале «ЗАНЯТО»).

Рассмотрим рекурсивный алгоритм определения π_k и m_k. Напомним, что i_k- число заявок типа k, k=1..n,

b_k- число канальных единиц, требуемых для выполнения заявки, типа k.

i- число канальных единиц, требуемое для выполнения всех заявок, всех типов

,

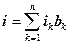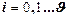(7.16)

P(i)- вероятность того, что в системе занято i канальных единиц.

Можно показать, что P(i) определяется рекурсивным соотношением[1].

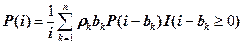, i=0,1…ϑ

(7.17)

Здесь I(i-b_k≥0) - функция, принимающая значение 1 при выполнении условия в аргументе и принимающая значения 0, в противном случае.

Используя (7.9) легко выразить значение P(i) через значение P(0)- вероятности отсутствия занятых каналов.

Далее применим алгоритм:

1) положим P(0)=1

2) выразим все вероятности P(i), (i=0,1…ϑ) через P(0), последовательно увеличивая i от 1 до ϑ.

3) находим значения показателей:

, , .
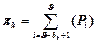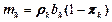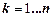