Выбор модели основан на анализе структуры сезонных колебаний

1) Если амплитуда колебаний примерно постоянна, то строят аддитивную модель.

2) Если амплитуда возрастает, то мультипликативную модель.

Основная задача эконометр. анализа - выявление каждой из компонент. В зависимости от наличия основной тенденции выделяют ряды:

- стационарные (ср. значение и дисперсия постоянны): x(k) є (µ,σ²), µ = const, σ² = const.

- нестационарные (содержат осн. тенденцию развития): x(k) є (µ,σ²), µ = var, σ² = const.

3) случайные члены ε_i должны быть независимы друг от друга.

Укажем самые распространенные методы анализа временных рядов.

Название метода	Характеристика метода
Спектральный анализ	Позволяет находить периодические составляющие временного ряда.
Корреляционный анализ	Позволяет находить сущ-ые периодические зависимости и соответствующие им задержки (лаги) как внутри 1го ряда (автокорреляция), так и между несколькими рядами (кросскорреляция).
Модели авторегрессии и скользящего среднего	Модели ориентированы на описание процессов, проявляющих однородные колебания, возбуждаемые случайными воздействиями. Позволяют предсказывать будущие значения ряда.
Многоканальные модели авторегрессии и скользящего среднего	Модели применяются в тех случаях, когда имеется несколько коррелированных между собой временных рядов. В них имеются колебания, возбуждаемые одной причиной. Позволяют предсказывать будущие значения ряда.
Сезонная модель Бокса-Дженкинса	Применяется, когда временной ряд содержит явно выраженный линейный тренд и сезонные составляющие. Позволяет предсказывать будущие значения ряда. Модель была предложена в связи с анализом авиаперевозок.
Прогноз экспоненциально взвешенным скользящим средним	Простейшая модель прогнозирования временного ряда. Применима во многих случаях. В том числе охватывает модель ценообразования на основе случайных блужданий.

Методы:Статистические (выделение/удаление тренда и сезонности) и динамические. К статистическим подходам относятся вероятностные модели. К динамическим — теория Такенса (Такенса-Мане)

ВР - серия числовых величин, полученных ч/з регулярные промежутки времени.

Идея: Факторы, влияющие на отклик изучаемой системы, действовали некоторым образом в прошлом и настоящем, и ожидается, что они будут действовать схожим образом и в не слишком далеком будущем. Цель ВР: оценка и вычленение этих влияющих факторов с целью прогноза дальнейшего поведения системы и выработки рациональных управленческих решений.

Факторы, влияющие на значения ВР: Тренд (изменение ВР). Циклическая компонента объясняет отклонения от тренда с период-ю от 2 до 10 лет. Сезонная компонента определяет короткопериодические колебания, связанные именно с изменениями внутригодовой активности, и повтор-ся через более или менее фиксир. моменты времени. Нерегулярная компонента (ошибка наблюдения) вызывает отклонения от хода отклика, опред-го трендовой, циклической и сезонной составляющими. Она может быть рассмотрена как случайная, и потому непрогнозируемая

Стационарные ВР – ряды, у которых вероятн. свойства не измен. с течением времени. Это такой ряд, который имеет постоянную среднюю, а значения ряда колеблются вокруг этой средней с некоторой постоянной дисперсией. Ряд 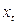называется строго стационарным (или стационарным в узком смысле), если совместное распред-е вероятностей m наблюдений 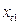, , 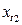, 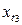…, 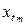такое же как и для m наблюдений 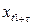, , 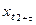, 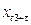…, , 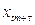для любых m, 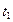, , 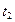…, 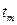и 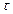. Свойства строго стационарных рядов не меняются при изменении начала отсчета времени. Ряд Xt называется слабо стационарным (или стационарным в широк см.), если его мат ожидание, дисперсия и ковариация не зависят от момента времени t:

1. E( 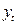) = µ -постоянное математическое ожидание

2. D( 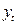)=y(0) - постоянная дисперсия

3. 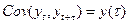- постоянная автоковариация.

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Автокорреляционная функция определяется интегралом: 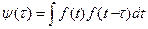и показывает связь сигнала (функции f(t)) с копией самого себя, смещённого на величину 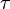., показывает характерные времена для исследуемых процессов

Автокорреляция – зависимость тек. значения случ. члена от непосредственно предшествующего значения. Т.о. автокорреляция случайного члена нарушает п.3. Причинами автокор-ции могут быть: ошибки спецификации (неправильно подобранная мат. ф-ция), необходимость введения в модель новой переменной, ошибки наблюдения. Наличие автокор-ции проверяется с помощью критерия Дарбина-Уотсона.

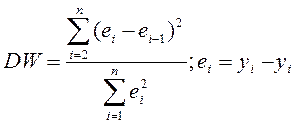
Значение статистики DW распределено в интервале (0,4). По таблице распределения статистики DW на основании уровня значимости α, объема выборки n и числа объясняющих переменных k находят критические точки d₁,d₂.

Проверка автокор-ции:

1. Формируется гипотеза Н₀ об отсутствии автокор-ции: 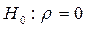, гипотезы H₁: 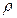> 0 о наличии положит. автокор-и и 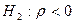о наличии отрицат. автокор-и.

2. Выбирается уровень значимости .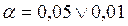

3. По табл распред-я DW на основании α, n и k находят критич-е т-и d₁ и d₂

4. На основании выбор. данных для построен. регрессии рассчит-ся значение DW:

- если 0 < DW < d₁, то с вероятностью 1- α принимается гипотеза Н₁,

- если d₁ < DW < d₂ , то нет оснований для принятия или не… всех гипотез,

- если d₂ < DW < 4-d₂, то с вероятностью 1- α принимается гипотеза Н_0,

- если 4-d₂ < DW < 4-d₁, то неопределенность,

- если 4-d₁ < DW < 4, то с вероятностью 1- α принимается гипотеза Н₂.

Если DW попадает в зону неопределенности, то для обнаружения автокор-ци исп-ся др методы. Если утверждается наличие автокор-ции, то пытаются ее устранить.