Погрешности цифровых телемеханических систем

Погрешности квантования.Цифровой метод передачи наряду с дискретизацией отсчетов по времени (ВРК) осуществляет квантование по уровню. Если в системе выбран шаг квантования d (расстояние между соседними уровнями квантования) и используется шкала параметра L, то число уровней квантования М (рисунок 2):

;

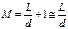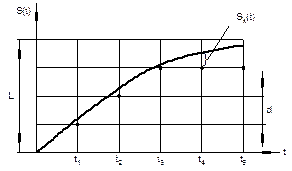
Рисунок 2. К определению ошибки квантования (e_k): e_k = S_k(t_i) – S(t_i); e_k < 0

В процессе квантования возможны три варианта привязки отсчетов:

– к ближайшему нижнему уровню,

– к ближайшему верхнему уровню,

– к ближайшему уровню (верхнему или нижнему).

На практике обычно используется привязка к ближайшему нижнему уровню. Привязка к уровню при отсчете приводит к появлению ошибки квантования (e_k). При привязке к нижнему уровню e_k всегда меньше 0.

Очевидно, что максимальное значение ошибки квантования по абсолютному значению равно шагу квантования d:

0 £ |e_k| £ d; e_{k max} = - d. (1)

Ошибка квантования может состоять из систематическойи случайной. Систематическую ошибку, которая представляет собой среднее значение ошибки, всегда можно учесть на приёмном конце телемеханической системы. Постоянная составляющая ошибки (систематическая ошибка) называется математическим ожиданием, обозначается М(e_k).

M (e_k) 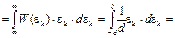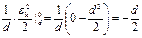; (2)

M (e_k) = ;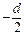

здесь 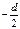- систематическая ошибка квантования при привязке к ближайшему нижнему уровню. Эта ошибка не опасна, т.к. она легко компенсируется на приемном конце телемеханической системы прибавлением к отсчету .

Более неприятна случайнаяошибка (рисунок 3.). Определим случайную среднеквадратическую погрешность квантования.

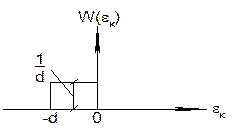
Рис. 3. К определению случайной среднеквадратической погрешности

; (3.)

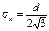. (3а.)

Как следует из (3.), среднеквадратическая погрешность s_k зависит лишь от шага квантования и не зависит от привязки отсчетов:

g_k = 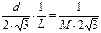. (4.)

Относительная среднеквадратическая ошибка квантования будет тем меньше, чем больше число уровней квантования М.

Погрешности, возникающие в результате помех в линии связи.В результате действия помех в линии связи может произойти ошибочный прием символа, т.е. при переданной «1» мы можем принять «0» (или наоборот). Очевидно, что вероятность искажения символа тем выше, чем больше уровень помех в линии связи. Если вероятность ошибочного приема символа, определяемая помехами в линии связи, равна p_ош, то вероятность правильного приема одного символа будет р¹_пр = 1 - p_ош.

Если же в кодовой комбинации n символов, то вероятность правильного приема такой комбинации:

р_пр =(1- р_ош)ⁿ @ 1 - n×р_ош . (5.)

Если для передачи используется не двоичный, а m-основный код, то для передачи того же числа уровней квантования потребуется не n, а n_m символов в кодовой комбинации, но тогда вероятность правильного приема такой кодовой комбинации составит.

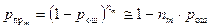. (5а.)

Поскольку вне зависимости от основания кода должна быть обеспечена передача любого из М уровней, то 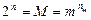; или 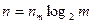, т.е. 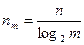; подставляя n_m в (5), получим

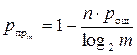. (6.)

Cравнивая (5) и (6), нетрудно видеть, что вероятность правильного приема кодовой комбинации при наличии помех в линии связи будет тем выше, чем больше основание m используемого кода. Полученный вывод в телемеханических системах реализуется лишь в особых случаях, т.к. приводит к значительному усложнению технической реализации телемеханических систем.

Значение параметра S, передаваемого цифровой системой, может быть представлено в виде

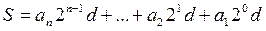, (7.)

где 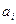- символы передаваемой кодовой комбинации; 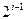- весовые коэффициенты разрядов; d – шаг квантования, принятый в цифровой системе.

Из (7) видно, что ошибка в отсчете, возникающая из-за искажения символа под действием помех в линии связи, зависит от того, в каком разряде произошло искажение. Если искажен символ младшего разряда, то ошибка будет минимальной: D_min = d.

Если же произошел ошибочный прием символа старшего разряда, то ошибка будет максимальной:

D_max= 2^n-1d = .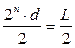

Определим среднеквадратическую ошибку, вызываемую искажением символов при приеме, с учетом того, что искажение любого символа равновероятно: 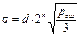; ; 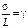; 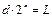тогда относительная среднеквадратическая ошибка 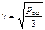. (8.)

Относительная среднеквадратическая ошибка, возникающая в результате искажения символа, зависит только от уровня помех в линии связи.

Критерии оценки точности телемеханических систем.Точность передачи параметров определяется погрешностями, которые возникают в процессе передачи и приема информации. Погрешности, возникающие при измерениях, делятся на случайные и систематические.

Систематическая погрешность, возникающая при каждом измерении и остающаяся постоянной, может быть учтена и компенсирована, например, вводом какой-либо константы. В инженерной практике больше неприятностей вносят случайные погрешности.

Если передается некоторый функциональный параметр f(t), то на приемном конце телемеханической системы мы получим некоторую похожую, но другую функцию Q(t), совпадающую с передаваемой функцией лишь в некоторых узловых точках (рисунок 3.). Погрешность D(t)=f(t)-Q(t). Значение максимальной погрешностиD_maxне характеризует в общем случае погрешность телемеханической системы.

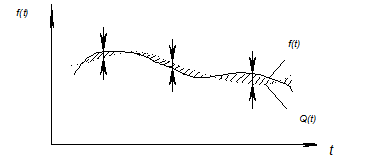
Рисунок 3. К определению погрешности телемеханической системы

Одним из наиболее точных показателей погрешности системы является среднеквадратическая погрешность s, которая по существу своему характеризует площадь, заключенную междуf(t)иQ(t):

. (9.)

Здесь .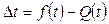

Для любой системы, если интервал Т₂ - Т₁ достаточно велик, т. е. среднеквадратическая погрешность вычисляется за достаточно большое время, значение среднеквадратической погрешности не зависит от реализации.

Реально в любой телемеханической системе есть целый ряд источников погрешности и, если они статистически независимы, то общая среднеквадратическая погрешность системы определяется выражением:

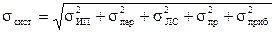, (10.)

где s_ип, s_пер, s_лс – погрешности измерительного преобразователя, передатчика, линии связи, приёмника, показывающего прибора.

В телемеханике широко пользуются понятием относительной среднеквадратической погрешности (g), приведенной к полной шкале параметра:

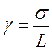, (11.)

где L=l_max - l_min – шкала параметра (пределы изменения измеряемых величин).

Для телемеханических систем относительная среднеквадратическая погрешность lчасто бывает задана. (Обычно в процентах).