Экстенсионал и интенсионал понятия

В семиотике для характеристики понятия и знаковой ситуации получили распространение категории денотата и концепта, а в ло­гике для тех же целей служат термины «экстенсионал» и «интен­сионал».

Одно и то же понятие может обозначать разные денотаты. Множество всех объектов, предметов или сущностей, являющихся денотатами понятия, составляет объем, или экстенсионал понятия. Если экстенсионал понятия Р обозначить через ext P, то можно записать выражение

extP=={e₁, e₂,.... е_n}, (8)

где e₁, e₂,.... е_n —сущности, являющиеся денотатами понятия Р.

Экстенсионал понятия — это совокупность всех его допустимых денотатов, соответствующих концепту этого понятия. Так, чтобы описать экстенсионал понятия АВТОМОБИЛЬ, следует рассмотреть класс автомобилей. Мы полагаем, что в концептуальном моделировании используют только конечные экстенсионалы понятия.

Разные понятия могут иметь один и тот же экстенсионал. Так, понятия «множество точек, равноудаленных от сторон данного угла» и «прямая, делящая угол на два равных угла», имеют одно и то же множество точек в качестве денотатов (биссектрису дан­ного угла). Эти понятия имеют общий экстенсионал, но выража­ют различный смысл, который мы связываем с их интенсионалами. Следовательно, понятие не полностью характеризуется экстенсионалом. Необходимо учитывать также интенсионала аспект понятия, который связан с его концептом.

Интенсионал понятия — это тот смысл, который мы вкладываем в данное понятие, т. е. интенсионал, характеризует концепт дан­ного понятия, его содержание. Интенсионал понятия Р будем обо­значать int P.

Возможны два подхода к формальному представлению интен­сионала: теоретико-множественный и логический. При теоретико-множественной формализации в интенсионал обычно включают множество всех дифференциальных признаков, характеризующих понятие.

Так, если понятие Р обладает некоторой совокупностью диф­ференциальных признаков (D₁, d¹), (D₂, d²),..., (D_n, dⁿ), где D_i— это имя дифференциального признака, a dⁱ—соответственно его значение, то интенсионал понятия Р можно представить в виде множества пар

int _s P={(D₁, d¹), (D₂, d²)..... (D_n, dⁿ)}. (9)

Здесь индекс S (от английского слова Set) у интенсионала означает его теоретико-множественную трактовку. Данный спо­соб чаще всего используется для формального представления ин­тенсионалов простых понятий. При этом под интенсионалом про­стого понятия Р понимают совокупность признаков, необходимых и достаточных для принятия решения о принадлежности некото­рой сущности экстенсионалу данного понятия.

Очевидно, что при таком способе представления схема понятия не содержится в его интенсионале, так как имена характери­стических и валентных признаков в выражении (9) отсутствуют.

Для сложных понятий более естественна логическая форма представления интенсионала. Так как широкий класс понятий может быть описан логическими формулами в виде хорновских дизъюнктов, то под интенсионалом понятия в этом случае обычно понимают правую часть импликации (6), т. е.

n

int _LP(X) = & P_i(X). (10)

i=1

Здесь индекс L (от английского слова Logic) у интенсионала означает его логическую формализацию.

Соответственно если понятие представлено логической форму­лой (7), то интенсионал может быть определен выражением

n m l

int _LP(X)=& D_i (d 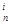, X) & Н_j (h 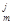, X) & V_k (v 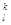,X). (11)

i=1 j=1 k=1

Очевидно, что при таком представлении интенсионал включа­ет также информацию о схеме понятия, хотя и не выделенную яв­ным образом.

Логическая форма представления интенсионала допускает сле­дующую интерпретацию: интенсионал понятия Р принимает ис­тинное значение на всех сущностях e_iÎextP. Так, на множестве точек «биссектриса угла» истинны оба утверждения: «равноуда­лены от сторон данного угла» и «делят данный угол на два рав­ных».

Связи между различными категориями, используемыми для описания понятий в логике и семиотике, представлены на рис. 2. 1.

понятие

Объем обозначение содержание

экстенсионал интенсионал имя

Рис. 2. 1. Связи между категориями, используемыми для описания понятий

Суммируя вышеизложенное, можно представить понятие в виде тройки

P=< int P, ext P, shm P >. (12)

Заключение

В зависимости от характера деятельности внимание проекти­ровщиков системы искусственного интеллекта концентрируется на различ­ных составляющих понятия: системные аналитики и администра­торы задач приложений, создающие концептуальную модель ПрО, больше должны опираться на интенсионал понятий ПрО, а администраторы базы знаний — на их схему. Тем самым понятие становится чрезвычайно удобным средством, которое позволяет, с одной стороны, путем использования интенсионала выразить семантические отношения для некоторого фрагмента реального мира, а с другой стороны, с помощью схемы обеспечить возможность перехода к менее детальному описанию и представлению этой ин формации в базе знаний.