Цифра код с избытком 3 код 4221

0 0011 0000

1 0100 0001

2 0101 0010

3 0110 0011

4 0111 1000

5 1000 0111

6 1001 1100

7 1010 1101

8 1011 1110

9 1100 1111

Эти коды обладают важным свойством: для того, чтобы для какой-либо цифры получить ее дополнение до 9, достаточно взять ее обратный код. Это позволяет упростить десятичную арифметику точно так же, как применение дополнительного кода упрощает двоичную арифметику. Вместо вычитания какого-либо числа достаточно произвести сложение с числом, которое представляет собой дополнение до 9 исходного числа плюс 1.

Пример: 27-15= 27

+85 (дополнение до 9 числа 15 = 84, затем прибавили 1)

Код Грея используется в механических шифраторах угла поворота вала. При переходе из любого его состояния к следующему изменяется лишь один разряд. Это позволяет предотвратить ошибки, так как в данном случае при переходе между двумя соседними значениями все разряды не могут измениться одновременно.

(0000) (1100)

(0001) (1101)

(0011) (1111)

(0010) (1110)

(0110) (1010)

(0111) (1011)

(0101) (1001)

(0100) (1000)

Представление чисел в соответствии с формулой

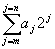
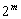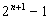называется представлением чисел с фиксированной точкой. Такой способ дает возможность при фиксированных значениях m и n представить числа в диапазоне от до . Например при m=0 и n=7, т.е. с помощью 8-разрядного двоичного кода можно представить числа в диапазоне от 0 до 255, а в случае необходимости представления отрицательных чисел, от -127 до +127. Такой диапазон представления чисел в ряде случаев оказывается недопустимо маленьким, что влечет за собой усложнение алгоритмов обработки данных с большим диапазоном изменения.

Для представления чисел в большом диапазоне изменения величин применяется т.н.формат с плавающей точкой. В этом формате число представляется в виде

,

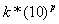где k называется мантиссой, а p - порядком числа. Значения k и p представляются в свою очередь в обычном формате с фиксированной точкой. Нетрудно видеть, что при использовании того же 8-разрядного двоичного кода для представления мантиссы и порядка, с помощью формата с плавающей точкой можно представить числа в диапазоне 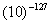о до 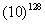. Налицо значительное увеличение диапазона изменения чисел, однако для их хранения необходимо уже не один, а два байта (для мантиссы и порядка).

Как и для формата с фиксированной точкой, при представлении чисел с плавающей точкой используются специальные алгоритмы арифметических операций над такими числами.

Шестнадцатеричная система счисления применяется для сокращения записи двоичных чисел. Каждые соседние 4 разряда в двоичной записи числа представляются в виде одного 16-ричного разряда. Для представления чисел от 10 до 15 применяются буквы от A до F.

Пример: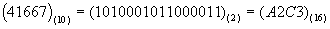

Шестнадцатеричное представление наилучшим образом соответствует байтовой структуре ЭВМ (1 байт = 8 бит). Один байт представляется в виде 2 шестнадцатеричных цифр. Чтобы преобразовать число из двоичной кода в шестнадцатеричный необходимо разбить код числа на группы из 4 бит начиная с младшего разряда и представить каждую группу в виде одной шестнадцатеричной цифры. Чтобы преобразовать число из шестнадцатеричного кода в двоичный необходимо последовательно записать каждую шестнадцатеричную цифру в виде 4 двоичных разрядов.

Лекция № 3

“Основные логические операции над двоичными числами. Синтез логических устройств. Таблицы истинности”.

Логические функции оперируют логическими переменными, т.е. переменными, принимающими только два значения - ИСТИНА и ЛОЖЬ (на математическом языке - 0 и 1). Результат логической функции может принимать тоже только эти два значения. Для представления логических функций используют аппарат логических уравнений и таблиц истинности.

Таблица истинности представляет собой таблицу в которой каждой комбинации входных логических переменных ставится в соответствие требуемое значение данной логической функции.

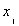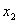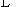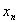				Y
		..
		..
..	..	..	..	..
		..

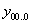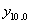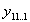Логические функции могут быть одной, двух и более логических переменных.

Элементарными логическими функциями являются следующие.

Функция “Логическое И”

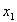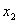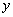Логическое уравнение: .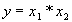

Схематическое изображение функции

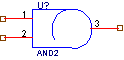
Функция “Логическое ИЛИ”

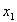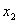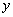Логическое уравнение: .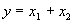

Схематическое изображение функции

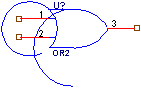
Функция “Логическое НЕ”

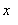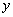Логическое уравнение: .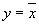

Схематическое изображение функции

Логические теоремы.

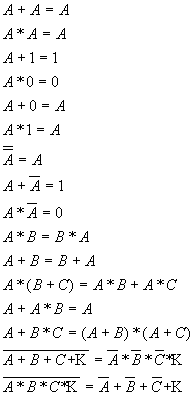
Используя данные теоремы, любую логическую функцию можно реализовать посредством блоков “И” и “НЕ” или “ИЛИ” и “НЕ”(это доказал Шеффер в 1913г.).

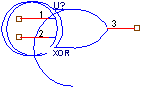
Пример: Функция “ИСКЛЮЧАЮЩЕЕ ИЛИ”.

Схематическое изображение функции

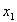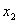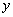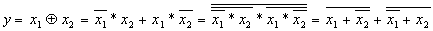
Обычно при постановке задачи логическую функцию представляют в виде таблицы истинности. Для получения уравнения логической функции и его минимизации используют метод “карт Карно”.

В соответствии с этим методом для получения уравнения логической функции необходимо:

1. Составить таблицу истинности функции в которой должны быть представлены все возможные сочетания входных сигналов и соответствующие им состояния выхода. В случае, когда состояние входа не оказывает влияния на выход, ставится X (любое значение).

2. Разбить все входные переменные на две группы произвольным образом.

3. Составить прямоугольную таблицу. Вдоль осей таблицы отложить последовательные состояния выделенных групп переменных в коде Грея.

4. Заполнить ячейки, расположенные на пересечении строк и столбцов таблицы значениями функции, соответствующими текущей комбинации состояний входных переменных.

5. Выделить в таблице все группы, содержащие 1 (либо 0).

6. Записать уравнение функции по выделенным группам.

Пример: Функция задана таблицей истинности.

A	B	C	Q

Составим карту Карно для данной функции.

	AB
C

Выделяем группы, содержащие “1”.

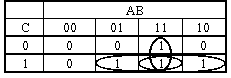
Согласно выделенным группам записываем уравнение логической функции.

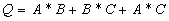
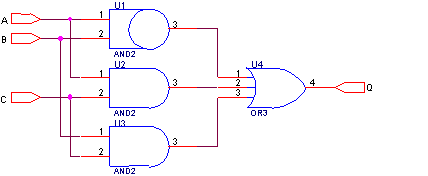
Схематическое изображение функции:

Рассмотрим основные виды комбинационных логических устройств.

Полным дешифраторомназывается устройство, имеющее n входов и выходов, причем каждой комбинации значений входных сигналов соответствует сигнал, равный 1, только на одном выходе. В качестве примера рассмотрим дешифратор на 2 входа. Его таблица истинности имеет вид.

X1	X2	Q0	Q1	Q2	Q3

Т.о., логические уравнения для соответствующих выходных разрядов дешифратора имеют вид:

; ; ; .

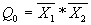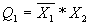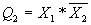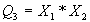Схема, реализующая подобное устройство имеет вид.

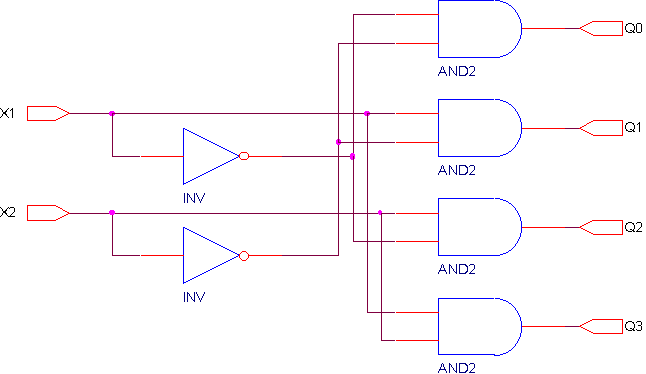
Полный дешифратор, дополненный общим разрешающим входом называется дешифратором-демультиплексором. Если добавить в рассмотренный дешифратор общий разрешающий вход E, то его уравнения примут вид:

; ; ; .

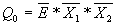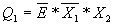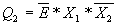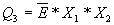Примером подобного дешифратора может служить микросхема 1533 ИД7 (74ALS138), представляющая собой дешифратор 3*8 с тремя входами общего разрешения: единичным G1, нулевыми G2AN и G2BN. Работа микросхемы разрешена если G1=1 & G2AN=0 & G2BN=0.

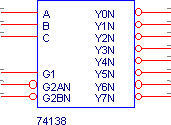
Т.о., дешифраторы осуществляют преобразование двоичного кода в унитарный код, т.е. код, только один из разрядов которого равен 1.

Шифраторы выполняют функцию обратную дешифраторам, т.е. преобразуют унитарный код в двоичный.

Таблица истинности шифратора на 4 входа имеет вид:

X1	X2	X3	X4	Q0	Q1

Уравнения для соответствующих выходов шифратора имеют вид:

;

.

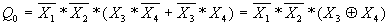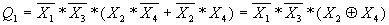Схема, реализующая указанные уравнения имеет вид.

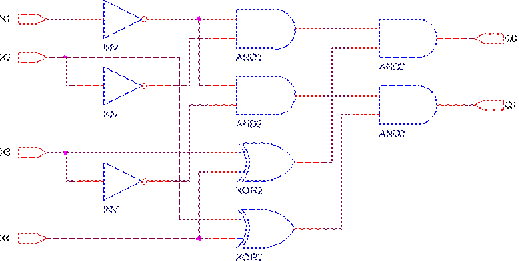
Мультиплексоромназывается комбинационная схема, имеющая m адресных и 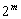информационных входов, а также один выход, на который подается сигнал с того информационного входа, чей адрес в данный момент присутствует на адресных входах. Рассмотрим мультиплексор на 2 входа X и Y с адресным входом S. Таблица истинности такого устройства имеет вид:

X	Y	S	Q

Этой таблице истинности соответствует следующее уравнение выхода

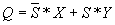
Этому уравнению соответствует схема.

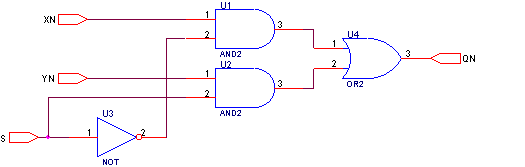
При добавлении общего разрешающего входа E получим устройство, называемое селектор-мультиплексор. При этом его уравнение примет вид

.

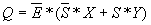Примером подобного устройства может служить микросхема 1533КП7 (74ALS151), представляющая собой селектор-мультиплексор на 8 каналов с общим входом разрешения G.

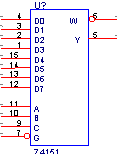
Демультиплексоры выполняют функцию, обратную мультиплексорам, т.е. производят коммутацию одного информационного входного сигнала на 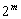выходов, где m - число адресных входов. Рассмотрим демультиплексор на 2 выхода. Его таблица истинности имеет вид:

X	S	Q0	Q1

Этой таблице истинности соответствуют уравнения выходов:

; .

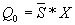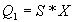Этим уравнениям соответствует схема.

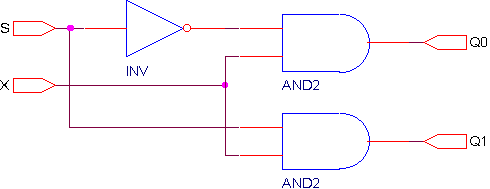
Создадим устройство для суммирования двух двоичных чисел 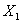и 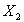. Опишем закон формирования младшего разряда суммы 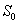и переноса в следующий разряд 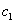с помощью таблицы истинности.

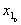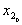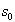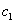Т.о. получим уравнения для младшего разряда суммы и переноса:

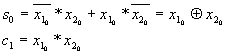
По полученным уравнениям получаем схему т.н. полусумматора.

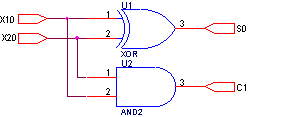
Обозначим разработанное устройство блоком S0.

Закон формирования любого следующего разряда суммы и разряда переноса в следующий разряд описывается таблицей истинности.

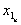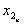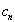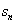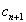Т.о. получаем уравнения для произвольного разряда суммы и переноса:

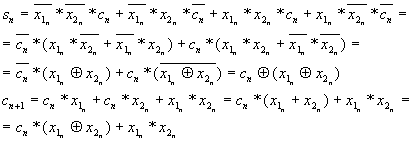
Т.о. получаем схему суммирования чисел произвольной разрядности.

Включая параллельно несколько подобных схем можно получить устройство для суммирования произвольного числа разрядов.

Создадим схему, реализующую преобразование прямого кода числа в его дополнительный код. Как известно для этого необходимо найти обратный код числа и прибавить к нему 1.

Схема, вычисляющая обратный код числа описывается уравнением

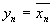
Эта схема называется “инвертор”.

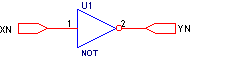
Обозначим это устройство как

Подав на один вход сумматора код с выхода инвертора, а на другой код числа “1”, на выходе сумматора получим дополнительный код числа.

Обозначим это устройство

Включив параллельно несколько схем вышеописанного мультиплексора получим мультиплексор на требуемое число разрядов.

Создадим устройство, способное складывать или вычитать два числа, в зависимости от состояния управляющего сигнала c.Для этого необходимо подать на один вход сумматора код одного из чисел, а на другой его вход подать либо прямой либо дополнительный код второго из чисел, в зависимости от состояния управляющего входа c. Такую коммутацию сигналов можно осуществить с помощью мультиплексора.

Разработанное устройство представляет собой примитивный прообраз арифметическо-логического устройства процессора.

Лекция № 4

“Последовательностные логические устройства.”

Все ранее рассмотренные схемы являются схемами мгновенного действия. Информация на их выходах меняется мгновенно с изменением информации на входах. Поэтому, они называются комбинационными. Однако, зачастую бывает необходим элемент, способный запоминать информацию о том, что какое-то событие имело место. Назовем егозапоминающим устройством (ЗУ).

Элементарной запоминающей ячейкой является триггер. Простейший, т.н. “R-S” триггер может быть построен с помощью двух логических элементов путем введения обратных связей.

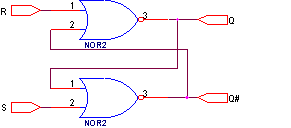
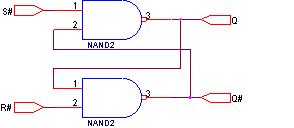
При подаче активного уровня на вход R на выходе Q устанавливается низкий уровень, а на выходе 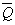- высокий уровень сигнала, и не меняется при дальнейших изменениях уровня сигнала на входе R. Аналогично, при подаче активного уровня на вход S, на выходе Q устанавливается высокий уровень, а на выходе 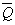- низкий. Одновременная подача активных уровней на оба входа запрещена. Простейший R-S триггер фиксирует информацию, поступившую на его входы в любой момент времени.

Как можно заметить, состояние выходных сигналов подобных схем зависит не только от входных, но и от выходных сигналов, запоминаемых устройством до прихода новой совокупности входных сигналов. Такие устройства называются последоватеностными схемами или конечными автоматами.

Работу триггерных схем можно описать с помощью таблиц, аналогичным ранее применявшимся таблицам истинности. Однако, в данном случае они называются таблицами переключений. Для простейшего RS-триггера Таблица переключений имеет вид:

Sn	Rn	Qn	Qn+1
			X
			X

Представленной таблице переключений соответствует следующая карта Карно:

Qn SnRn
			X
			X

Если позиции, соответствующие неопределенным состояниям заполнить единицами, то получим функцию RS-триггера с инверсными входами:

;

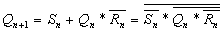Если неопределенные позиции заполнить нулями, то получим уравнение RS-триггера с прямыми входами:

;

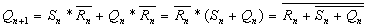Оба приведенных типа триггеров имеют запрещенное состояние входных сигналов 11, приводящее к несанкционированному переключению выхода в 0 или 1.

Если заполнить неопределенные позиции комбинацией 01, то получим уравнение т.н. E-триггера:

;

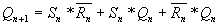Этот триггер не имеет запрещенных комбинаций. Комбинация входных сигналов 11 не меняет состояние выходных сигналов.

Если заполнить неопределенные позиции комбинацией 10, то получим уравнение т.н. JK-триггера:

;

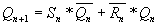JK-триггер является часто используемым, поэтому для отличия от RS-триггера его входы не S и R, а J и K соответственно. Поэтому уравнение JK-триггера можно переписать так:

;

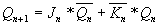Этот триггер характерен тем, что комбинация входных сигналов 11 приводит к инвертированию выходных сигналов. Данное свойство этого триггера позволяет ему работать в т.н. “счетном” режиме. Для этого необходимо объединить входы J и K. При этом каждый входной импульс будет приводить к инвертированию выходного сигнала. Триггер, работающий в счетном режиме называют Т-триггером.

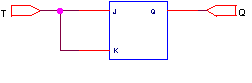
Уравнение Т-триггера получим произведя замену J=K=T в последнем уравнении:

;

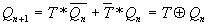Объединив последовательно несколько Т-триггеров можно получить простейший двоичный счетчик или делитель частоты.

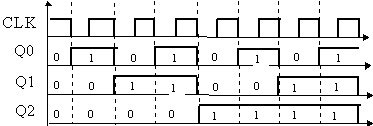
Подобные счетчики обладают пониженным быстродействием т.к. каждый триггер вносит некоторую задержку при прохождении счетных импульсов.

Из-за конечного времени переключения логических элементов и задержки срабатывания в логических схемах возможны т.н. “гонки сигналов” - переходные режимы, вызванные тем, что из-за задержек поступления информации выходной сигнал на некоторое время принимает ложные значения. Рассмотрим эти режимы на примере схемы, реализующей функцию .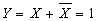

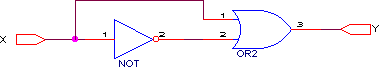
Теоретически выходной сигнал такой схемы Y должен быть всегда равен 1 и не изменяться при изменении входного сигнала X. Однако в реальной схеме инвертор имеет конечное время распространения сигнала, из-за чего сигнал на второй вход элемента “И-НЕ” приходит несколько позже чем на первый. Т.о. существует короткий интервал времени, в течение которого комбинация входных сигналов логического элемента соответствует нулевому уровню выходного сигнала.

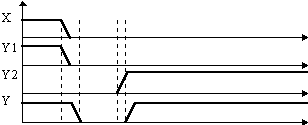
Подобные ситуации могут приводить к ложным срабатываниям триггеров и нарушению алгоритма работы устройства. Устранить ошибки, возникающие за счет “гонок сигналов” в логических цепях можно за счет временного стробирования. Вырабатываемый логическим устройством сигнал в этом случае передается на последующие устройства не непрерывно и не в произвольные моменты времени, а только в такие моменты времени, когда искажение правильных значений выходного сигнала за счет “гонок” заведомо исключено.

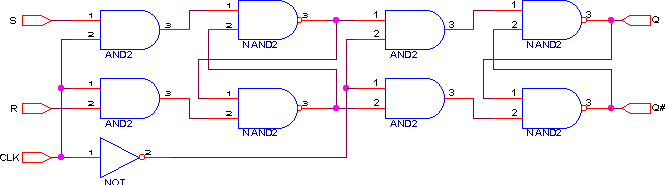
Временное стробирование обеспечивается с помощью схем совпадения (схем “И” или “И-НЕ”). В течение времени стробирования на один вход схемы “И” действует стробирующий импульс, а на второй - сигнал логического устройства. Обычно стробирующие сигналы действуют периодически. Их называют тактовымиилисинхронизирующими. Период следования тактовых импульсов называюттактом логического устройства. Триггеры, работающие с использованием синхронизирующих сигналов, называютсинхронными. Схема синхронного RS-триггера имеет вид:

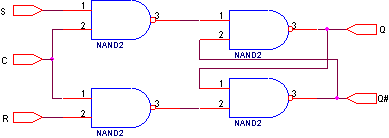
Основой схемы служит асинхронный RS-триггер с инверсными входами. Сигнал на каждый вход триггера подается через схему “И-НЕ”. При активном единичном уровне синхросигнала C сигналы со входов S и R передаются на соответствующие входы триггера, а при нулевом уровне синхросигнала на обоих входах триггера устанавливается неактивный единичный уровень сигналов. Т.о., синхронный R-S триггер, в отличие от него, обеспечивает фиксацию информации только при активном состоянии на входе синхронизации. Логическая функция синхронного RS-триггера имеет вид:

;

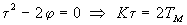Состояние в синхронных триггерах может измениться только во время действия синхроимпульса. В промежутках между синхроимпульсами выходные напряжения постоянны. Это свойство позволяет создать на основе синхронных RS-триггеров триггеры задержки - D-триггеры (Delay Trigger). D-триггер фиксирует информацию, приходящую на один вход данных. У D-триггера значение выходного сигнала в (n+1) такте равно значению входного сигнала в n такте. Т.о., D-триггер запоминает состояние входного сигнала на период одного такта квантования. Схема D-триггера имеет вид:

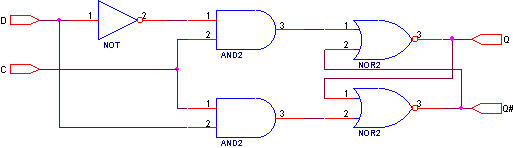
Он выполняет логическую функцию:

;

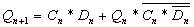Из D-триггера можно получить счетный T-триггер, подав на вход D сигнал с инверсного выхода.

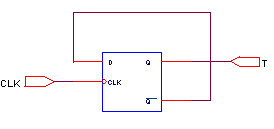
Описанные типы триггеров пропускают входной сигнал на выход в течение всего активного периода сигнала синхронизации.

Двухступенчатый триггер никогда непосредственно не пропускает входной сигнал на выход.

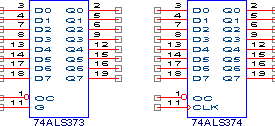
Синхронные триггеры выпускаются в виде отдельных микросхем, примерами которых могут служить КР1533ТВ9 (74ALS112) - двойной JK-триггер, КР1533ТМ2 (74ALS74) - двойной D-триггер и др.

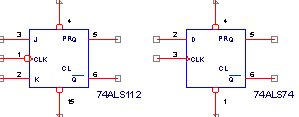
Объединив несколько D-триггеров с единым входом синхронизации можно получить регистр, способный фиксировать многоразрядную информацию. В соответствии со структурой внутренних триггеров существуют регистры-защелки и регистры с синхронным стробированием. Регистры-защелки пропускают входную информацию на выход при одном уровне сигнала синхронизации и фиксируют ее при переходе сигнала синхронизации в другое состояние. Регистры с синхронным стробированием фиксируют информацию по фронту сигнала синхронизации. Примерами таких регистров могут служить микросхемы КР1533ИР22 (74ALS373) - 8-разрядный регистр-защелка и КР1533ИР23 (74ALS374) - 8-разрядный регистр, фиксирующий информацию по переднему фронту сигнала синхронизации.

Функции переходов рассмотренных типов триггеров можно получить из уравнений этих триггеров если в них положить С=1. Они имеют вид:

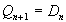- для D-триггера;

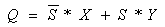- для JK-триггера;

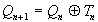- для Т-триггера.

Отсюда можно вывести функции возбуждения каждого из перечисленных типов триггеров, которые определяют какие значения должны быть установлены на управляющих входах в предыдущем такте квантования для того, чтобы в следующем такте на выходе триггера установился сигнал заданного значения. Эти функции имеют вид:

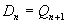- для D-триггера;

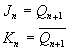- для JK-триггера;

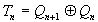- для Е-триггера.

Представленные функции используются для синтеза конечных автоматов. Продемонстрируем процесс синтеза на примере создания двоичного счетчика. Составим таблицу переключений счетчика в которой представим последовательные комбинации выходов счетчика и комбинации, следующие за текущей.

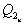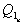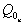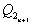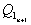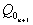После этого можно составить карты Карно и определить уравнения зависимостей последующих состояний разрядов счетчика от предыдущих.

;

;

;

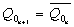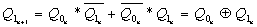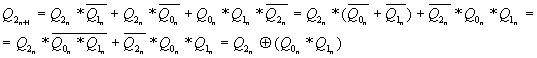Подставляя теперь эти уравнения в выражения для функций возбуждения получим уравнения для цепей, формирующих управляющие сигналы триггеров соответствующих разрядов счетчика. В случае реализации счетчика на Т-триггерах получим:

;

;

.

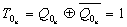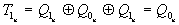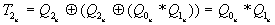Эти уравнения соответствуют следующей схеме.

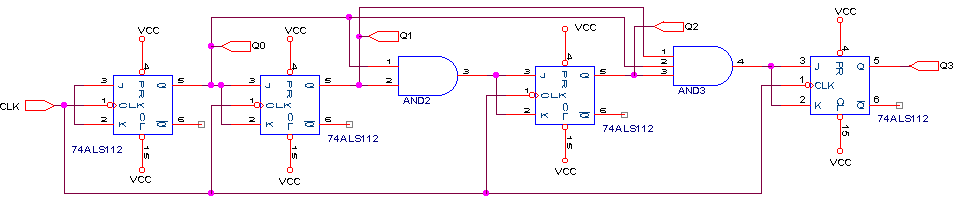
В случае реализации счетчика на D-триггерах получим уравнения:

;

;

.

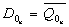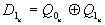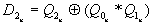Эти уравнения соответствуют следующей схеме.

Аналогичным образом можно осуществить синтез двоично-десятичных, вычитающих, реверсивных и других типов счетчиков. Подобные счетчики называются синхронными, т.к. сигнал синхронизации подается одновременно на все триггеры. Такие устройства выпускаются серийно в виде отдельных микросхем, примерами которых могут служить КР1533ИЕ9 (74ALS160) - 4-разрядный двоично-десятичный синхронный счетчик, КР1533ИЕ10 (74ALS161) - 4 разрядный двоичный синхронный счетчик и др.

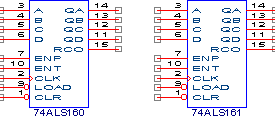
Данные устройства имеют параллельную предзагрузку данных через входы A, B, C, D и строб загрузки LOAD, а также сброс в нулевое состояние по сигналу CLR. Выход переноса в следующий разряд RCO устанавливается в нулевое состояние если текущее состояние счетчика является последним (1111 - для двоичных и 1001 - для двоично десятичных). Включая последовательно несколько таких устройств можно создавать многоразрядные синхронные счетчики.

Если объединить несколько D-триггеров по цепочке, соответствующей уравнению 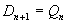, то получим т.н. регистр сдвига.

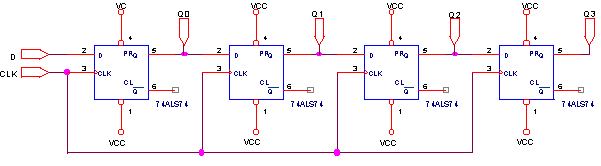
Они используются как устройства с последовательным вводом данных (для ввода N-разрядного двоичного слова необходимо n тактов квантования), а также для выполнения операций умножения или деления на 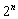путем сдвига двоичного слова на n разрядов в лево или вправо соответственно.

Лекция № 4

Основными операциями в памяти, в общем случае, являются:

-запись - занесение информации в память;

-считывание - выборка информации из памяти.

Основными характеристиками систем памяти являются:

- информационная емкость - максимально возможное количество байтов хранимой информации;

- ширина выборки (разрядность) - количество разрядов информации, записываемых в ЗУ или извлекаемых из него за одно обращение;

- время обращения (быстродействие) - характеризуется временем цикла обращения к ЗУ, т.е. интервалом времени от момента поступления кода адреса до установления информации на выходе.

- способность сохранения информации при отключения питания.

По способу организации доступа к памяти различают ЗУ с произвольным доступом (адресные) и ЗУ с последовательным доступом (безадресные).

По способу хранения информации различают статические и динамические ЗУ.

По функциональному назначению различают сверхоперативные ЗУ (СОЗУ), оперативные ЗУ (ОЗУ), постоянные ЗУ (ПЗУ), перепрограммируемые постоянные ЗУ (ППЗУ), стековые ЗУ.

СОЗУ представляют собой набор регистров, содержание которых непосредственно используется при обработке информации в микропроцессоре. СОЗУ встроено в БИС микропроцессора и предназначено для хранения команд, операндов и результатов промежуточных вычислений. Разрядность СОЗУ соответствует разрядности микропроцессора.

ОЗУ предназначено для хранения оперативной (переменной) информации, требующейся в процессе обработки. ОЗУ разделяют на динамические и статические. Элементарная ячейка динамического ОЗУ базируется на конденсаторе.

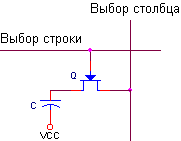
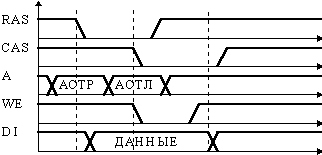
Подобные запоминающие ячейки расположены в виде матрицы на пересечении линий связи, называемых соответственно столбцами и строками. Во время цикла записи конденсатор заряжается до “0” или “1” от шины выбора столбца при активном состоянии сигнала выбора ряда. Во время цикла чтения заряд конденсатора передается через открытый транзистор и шину выбора столбца на выходные усилители, и дальше, на выход. Утечки емкости, а также ее разряд во время цикла чтения обуславливают необходимость регенерации информации, которая заключается в последовательном переборе адресов строк. Примером динамического ОЗУ может служить микросхема К565РУ7.

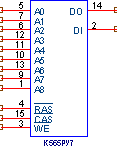
Ее основные характеристики:

Емкость - 256 Кбит.

Разрядность - 1 бит.

Время цикла “запись/чтение” - около 300 нс.

Диаграмма цикла записи данных имеет вид.