Граф, в котором две любые вершины соединены ровно одним простым путём, является деревом
Доказательство:
Очевидно, что данный граф связен. Предположим, что в нем есть цикл. Тогда любые две вершины этого цикла соединено, по крайней мере, двумя простыми путями. Получили противоречие, а значит, наше предположение неверно.
*Дерево – это граф, в котором две любые вершины соединены ровно одним простым путём.
ЛЕММА (о висячей вершине) В каждом дереве есть висячая вершина.
Доказательство:
Рассмотрим произвольную вершину дерева и пойдём по любому выходящему из неё ребру в другую вершину. Если из новой вершины больше рёбер не выходит, то мы остаёмся в ней, а противном случае, идём по любому другому ребру дальше. Понятно, что в этом путешествии мы никогда не сможем попасть в вершину, в которой уже побывали: это означало бы наличие цикла. Так как у графа конечное число вершин, то наше путешествие обязательно должно закончится. Но закончиться оно может только в висячей вершине. Лемма доказана.
ТЕОРЕМА. В дереве число вершин на одну больше числа ребер.
Доказательство:
Из условия теоремы граф – дерево. У него есть висячая вершина. Удалим её и выходящее из нее ребро. Оставшийся граф также дерево. У него есть висячая вершина, которую также удалим. Проделав эту операцию n-1 раз, получим граф, состоящий из одной вершины. Т. к. удалялось по одному ребру, то вначале их было n-1.
6. Изоморфизм. Плоские графы и теорема Эйлера.
Два графа называются изоморфными, если у них поровну вершин, и вершины каждого графа можно занумеровать числами от 1 до n, так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие вершины второго графа.
Докажем, что графы изображенные на рисунке 11 изоморфны.
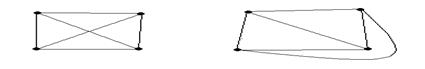
рис.11
Пронумеруем вершины первого и второго графов от 1и до 4.(рис.12)
рис.12
В первом графе соединены вершины 1 и 2, 2 и 3, 3 и 4, 1 и 4, 1 и 3, 2 и 4; заметим, что во втором графе также соединены вершины 1 и 2, 2 и 3, 3 и 4, 1 и 4, 1 и 3, 2 и 4, следовательно, данные графы изоморфны.
Для того, чтобы выяснить, изоморфны ли два графа, нужно убедиться в том, что у них:
одинаковое количество вершин
если вершины одного графа соединены ребром, то и соответствующие им вершины другого графа тоже соединены ребром. Граф, который можно нарисовать так, чтобы его рёбра не пересекались нигде, кроме вершин, называются плоским или планарным.
ТЕОРЕМА Эйлера. Для правильно нарисованного связного плоского графа имеет равенство: V-E+F=2, где V – число вершин, E - число рёбер, F – число кусков. (равенство V-E+F=2 обычно называют формулой Эйлера)
Доказательство:
Будем удалять рёбра графа до тех пор, пока не получим дерево. Посмотрим, как при удалении очередного ребра изменяются величины V, E и F. Ясно, что число вершин не изменяется, а количество рёбер уменьшается на один. Число кусков также уменьшается на один, так как при удалении ребра два примыкающих к нему куска сливаются в один. Поэтому V-E+F при такой операции не изменяется. Так как для полученного дерева V-E=1 и F=1, то V-E+F=2 и, следовательно, для исходного графа также выполняется это равенство. Значит, теорема доказана.
Граф, каждая вершина которого соединена с ребром любой другой вершины, называется полным.
ТЕОРЕМА Понтрягина – Куратовского: Граф является плоским тогда и только тогда, когда он не содержит (в топологическом смысле) графа с шестью вершинами типа «домики-колодцы» и полного графа с пятью вершинами. (В основном используется старинных задач о домах и колодцах, суть которой сводится к выяснению вопроса — является ли рассматриваемый граф плоским или нет, рис.13)
рис.13
Ориентированные графы
Существуют значительные классы практических задач, которые решить с помощью ранее рассмотренных типов графов невозможно. Так, например, схема дорог и площадей города изображается с помощью плоского графа. Но если нужно этой схемой воспользоваться с целью проезда по городу на автомашине, а движение на отдельных (или на всех) улицах одностороннее? Тогда могут помочь сориентироваться в этой ситуации стрелки, расположенные, например, прямо на ребрах-улицах рассматриваемой схемы (графа) города.
Граф, на рёбрах которого расставлены стрелки, называется ориентированным.
Степенью выхода вершины ориентированного графа называется число ребер, для которых эта вершина является началом (число ребер, «выходящих» из вершины).
Степенью входа вершины ориентированного графа называется число ребер, для которых эта вершина является концом (число ребер, «входящих» в вершину).
рис.14
Так, на рисунке 15 изображен ориентированный граф АБВГД. Степени входа и выхода некоторых его вершин такие:
Ст.вх.А=2, Ст.вых.А=1
Ст.вх.В=2, Ст.вых.В=0
Ст.вх.Д=1, Ст.вых.Д=3
Путем, в ориентированном графе от вершины А1 к вершине An называется последовательность ориентированных ребер
A1A2, A2A3, ..., Аn-1Аn в которой конец каждого предыдущего ребра совпадает с началом следующего и каждое ребро встречается в этой последовательности только один раз.
На ниже приведенном рисунке показаны примеры путей в ориентированном графе. Причем, первые два пути— простые — ни одна из вершин не содержится в нем более одного раза. Третий путь не является простым, т. к. через вершину Г путь «проходил» дважды. (рис.15)
рис.15
Ориентированным цикломназывается замкнутый путь в ориентированном графе.
На предыдущем рисунке приведены примеры ориентированных циклов в последних двух графах. Цикл, как и любой другой путь в графе, имеет длину, которая определяется числом ребер в этом пути.
рис.16
Так, на рисунке 16 пути от А к Д могут быть различны и иметь различную длину.
Первый путь имеет длину 2, второй - 3,
а третий — 4.