Алгоритм формирования комбинаций циклического (n, k)-кода
При построении двоичных циклических кодов кодовые комбинации длины n принято представлять в виде полиномов степени (n -1):
F(x) = an-1xn-1 + an-2xn-2 + ...+ a1x + a0,
где a0, a1, ...,an-1 - коэффициенты, принимающие значения 0 или 1.
Например, кодовую комбинацию 1001101 можно записать в виде:
F(x) = x6 + x3 + x2 + 1.
Поэтому циклические коды часто называют полиномиальными кодами.
Название циклического кода происходит от его основного свойства, заключающегося в том, что циклический сдвиг элементов разрешенной кодовой комбинации дает также разрешенную кодовую комбинацию, принадлежащую этому же циклическому коду (например, 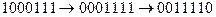 и т. д.).Другое свойство циклического кода состоит в том, что при суммировании по модулю два (mod2) двух разрешенных кодовых комбинаций также образуется разрешенная кодовая комбинация.
и т. д.).Другое свойство циклического кода состоит в том, что при суммировании по модулю два (mod2) двух разрешенных кодовых комбинаций также образуется разрешенная кодовая комбинация.
Циклический код в его полиномиальном представлении можно определить как множество многочленов степени (n -1) и меньше, каждый из которых делится без остатка на некоторый многочлен P(x) степени r, называемый образующим или порождающим многочленом кода.
Порождающий многочлен циклического кода, исправляющего однократные ошибки, должен быть неприводимым, то есть не должен делиться ни на какой другой полином с двоичными коэффициентами и, как правило, должен быть примитивным [3].
Рассмотрим построение комбинации систематического циклического (n,k)-кода. Будем полагать, что порождающий многочлен задан. Алгоритм формирования циклического кода будет следующим:
1) G(x)x(n - k), то есть информационный полином G(x) умножается на x в степени равной степени порождающего многочлена r = (n - k). Умножение полинома на xr означает сдвиг на r разрядов влево.
2) 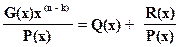 , то есть произведениеG(x)x(n-k) делится на порождающий многочлен P(x) и определяется частное Q(x) и остаток от деления R(x). Степень R(x) всегда ниже степени порождающего многочлена.
, то есть произведениеG(x)x(n-k) делится на порождающий многочлен P(x) и определяется частное Q(x) и остаток от деления R(x). Степень R(x) всегда ниже степени порождающего многочлена.
3) F(x) = G(x)x(n-k) 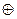 R(x), то есть комбинация циклического кода строится как совокупность информационных элементов и приписанных к ним со стороны младших разрядов элементов остатка (проверочных элементов).
R(x), то есть комбинация циклического кода строится как совокупность информационных элементов и приписанных к ним со стороны младших разрядов элементов остатка (проверочных элементов).
Рассмотрим пример построения циклического кода для информационного полинома вида G(x) = x4 + x2 + x. Этот информационный полином G(x) соответствует двоичной кодовой комбинации 10110.
Пусть порождающий многочлен имеет вид: P(x) = x4 + x + 1. В соответствии с неравенством (1) максимальная длина кодовой комбинации циклического кода n = 2r - 1 равна 15 (полный код). Однако, на практике часто выбирают длину комбинации n1 < 2r - 1. Образующийся при этом циклический код называют укороченным. Следует иметь ввиду, что укорочение происходит за счет уменьшения числа информационных разрядов k.
Корректирующая способность укороченного циклического кода не ниже корректирующей способности исходного полного циклического кода. Техника кодирования и декодирования в обоих случаях одна и та же. Однако, циклический сдвиг элементов разрешенной кодовой комбинации укороченного циклического кода не всегда приводит к образованию разрешенной кодовой комбинации. Поэтому укороченные коды относят к числу псевдоциклических.
В нашем примере разрядность исходного кода (информационного полинома G(x)) равна 5. Число проверочных разрядов определяется степенью порождающего многочлена (у нас - это 4). В итоге разрядность комбинации циклического кода равна 9, то есть мы получим укороченный код (9, 5).
Выполним первую операцию построения систематического циклического кода - умножения на x4 информационного полинома G(x). Получим полином G(x)x4 = x8 + x6 + x5.
Умножению информационного полинома G(x) на x4 соответствует добавление справа четырех нулей к двоичному представлению G(x), т.е. 101100000.
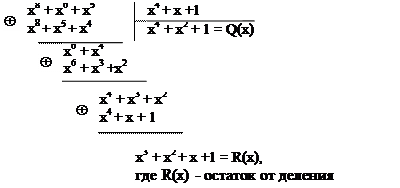 Вторая операция - деление G(x)x4 на порождающий многочлен P(x):
Вторая операция - деление G(x)x4 на порождающий многочлен P(x):
Здесь операция вычитания заменяется операцией сложения по mod 2. Операция суммирования по mod 2 выполняется по следующему алгоритму:
1 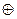 1 = 0; 0
1 = 0; 0 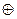 0 = 0; 1
0 = 0; 1 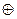 0 = 1; 0
0 = 1; 0 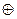 1= 1
1= 1
Та же операция деления в двоичном коде имеет вид:
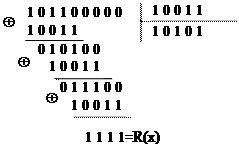 |
Третья операция - построение комбинации циклического кода F(x):
F(x) = G(x)x(n-k) 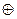 R(x) =
R(x) = 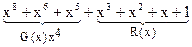
Полученный результат в двоичном коде имеет вид:
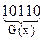
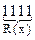
Сделаем проверку полученного циклического кода, представленного полиномом F(x), делением этого полинома на порождающий многочлен P(x). Остаток от деления должен быть нулевым.
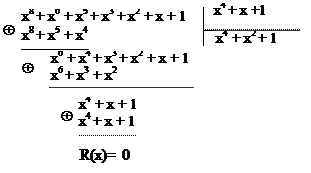 |

Та же операция в двоичном коде:
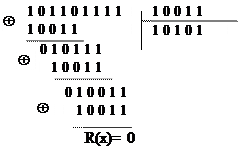 |
Итак, для заданного информационного кода G(x) разрядностью 5 получен укороченный циклический код разрядностью 9, т. е. код (n, k) = (9, 5). Минимальное кодовое расстояние (расстояние Хэмминга) для этого кода равно dmin = 3, то есть он позволяет обнаруживать все ошибки кратностью s 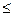 2 или исправлять однократные ошибки (t = 1). В режиме обнаружения данный код может обнаруживать и часть ошибок более высокой кратности.
2 или исправлять однократные ошибки (t = 1). В режиме обнаружения данный код может обнаруживать и часть ошибок более высокой кратности.
Общее число кодовых комбинаций рассматриваемого кода Nобщ = 29 = 512; число разрешенных кодовых комбинаций Nразр = 25 = 32; число запрещенных кодовых комбинаций Nзапр = Nобщ - Nразр = 480.
Избыточность данного кода равна 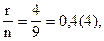 а кодовая скорость -
а кодовая скорость - 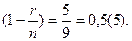
Для получения всех ненулевых разрешенных комбинаций (для кода (9,5) – это 25-1=31) составляют порождающую матрицу 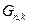 называемую также образующей или производящей матрицей, которая состоит из единичной матрицы
называемую также образующей или производящей матрицей, которая состоит из единичной матрицы 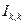 размерности k,k (для кода (9,5) – это 5,5) и матрицы
размерности k,k (для кода (9,5) – это 5,5) и матрицы 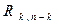 проверочных элементов размерности k,n-k (для кода (9,5) – это 5 , 4).
проверочных элементов размерности k,n-k (для кода (9,5) – это 5 , 4).
Единичная матрица имеет вид:
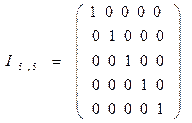
Для нахождения строк матрицы 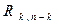 проверочных элементов выполняется деление многочлена вида
проверочных элементов выполняется деление многочлена вида 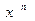 на порождающий многочлен. Полученные на каждом шаге деления остатки и являются строками проверочной матрицы
на порождающий многочлен. Полученные на каждом шаге деления остатки и являются строками проверочной матрицы 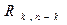 . Пример получения проверочных элементов для кода (9,5) и порождающего многочлена P(x)=10011 имеет вид:
. Пример получения проверочных элементов для кода (9,5) и порождающего многочлена P(x)=10011 имеет вид:
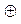



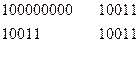
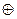
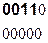



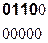

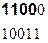

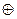
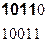
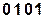

Порождающая матрица для рассматриваемого примера будет иметь вид:
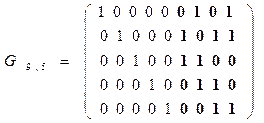
Каждая строка этой матрицы является разрешенной кодовой комбинацией кода (9,5). Для получения остальных разрешенных кодовых комбинаций необходимо каждую строку матрицы 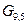 сложить по mod2 с каждой строкой, затем с двумя строками, с тремя и т.д.Например, сложение первой строки со второй даст разрешенную комбинацию вида: 110001110, сложение всех пяти строк также даст разрешенную комбинацию вида: 111110111.
сложить по mod2 с каждой строкой, затем с двумя строками, с тремя и т.д.Например, сложение первой строки со второй даст разрешенную комбинацию вида: 110001110, сложение всех пяти строк также даст разрешенную комбинацию вида: 111110111.
Для определения минимального кодового расстояния 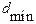 циклического кода (n,k) следует составить его проверочную матрицу
циклического кода (n,k) следует составить его проверочную матрицу 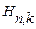 , которая получается путем транспонирования (замены местами строк и столбцов) матрицы проверочных элементов
, которая получается путем транспонирования (замены местами строк и столбцов) матрицы проверочных элементов 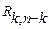 с последующим дописыванием справа элементов единичной матрицы размерностью (n-k). В нашем случае проверочная матрица циклического кода (9,5) имеет вид:
с последующим дописыванием справа элементов единичной матрицы размерностью (n-k). В нашем случае проверочная матрица циклического кода (9,5) имеет вид:
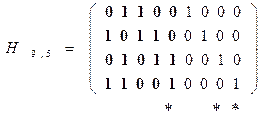
Минимальное кодовое расстояние 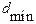 равно минимальному числу столбцов, построчная сумма по mod2 элементов которых дает нулевой столбец.
равно минимальному числу столбцов, построчная сумма по mod2 элементов которых дает нулевой столбец.
При наличии двух одинаковых столбцов в проверочной матрице 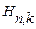 минимальное кодовое расстояние
минимальное кодовое расстояние 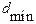 =2, а при их отсутсутствии-
=2, а при их отсутсутствии- 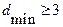 и определяется путем перебора.
и определяется путем перебора.
Для кода (9,5) минимальное число столбцов, дающее при построчном суммировании по mod2 нулевой столбец, равно трем (эти столбцы отмечены знаком (*) в матрице 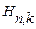 ). Следовательно, минимальное кодовое расстояние циклического кода (9,5)
). Следовательно, минимальное кодовое расстояние циклического кода (9,5) 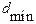 =3, что позволяет ему гарантированно исправить однократную или обнаружить двукратную ошибку.
=3, что позволяет ему гарантированно исправить однократную или обнаружить двукратную ошибку.
