Погрешности компьютерного математического моделирования, способы их оценки

При численном решении математических и прикладных задач почти неизбежно появление на том или ином этапе их решения погрешностей следующих трех типов:

1) Погрешность задачи. Она связана с приближенным характером исходной содержательной модели (в частности, с невозможностью учесть все факторы в процессе изучений моделируемого явления), а также ее математического описания, параметрами которого служат обычно приближенные числа (например, из-за принципиальной невозможности выполнения абсолютно точных измерений). Для вычислителя погрешность задачи следует считать неустранимой (безусловной), хотя постановщик задачи иногда может ее изменить.

2) Погрешность метода. Это погрешность, связанная со способом решения поставленной математической задачи и появляющаяся в результате подмены исходной математической модели другой или конечной последовательностью других, например, линейных моделей. При создании численных методов закладывается возможность отслеживания таких погрешностей и доведения их до сколь угодно малого уровня. Отсюда естественно отношение к погрешности метода как к устранимой (или условной).

3) Погрешность округлений (погрешность действий). Этот тип погрешностей обусловлен необходимостью выполнять арифметические операции над числами, усеченными до количества разрядов, зависящего от применяемой вычислительной техники и используемого типа данных (если, разумеется, не применяются специальные программные средства, реализующие, например, арифметику рациональных чисел).

Все три описанных типа погрешностей в сумме дают полную погрешность результата решения задачи.

Рассмотрим некоторые возможные подходы к учету погрешностей действий.

Пусть А и а — два «близких» числа; условимся считать А точным, а приближенным.

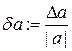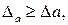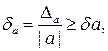Величина Dа:=| А-а| называется абсолютной погрешнотью приближенного числа а, а — его относительной погрешностью. Числа D_а и d_а, такие, что и называются оценками или границами абсолютной и относительной погрешностей соответственно (к D_а и d_а часто применяют также термин «предельные погрешности»). Так как обычно истинные погрешности неизвестны, то там, где не может возникнуть недоразумений, будем иногда называть D_а и d_а просто абсолютной и относительной погрешностями.

Поставим вопрос о грубом оценивании погрешности результата при вычислении значения дифференцируемой функции u = f(x₁,x₂, ××× , x_п)приближенных аргументов x₁,x₂, ××× , x_п если известны границы их абсолютных погрешностей соответственно. В этом случае точные значения аргументов 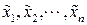лежат соответственно на отрезках [ 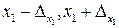], [ ], 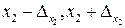¼, [ 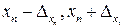]. точная абсолютная погрешность результата u =f(x₁,x₂, ××× , x_п)есть

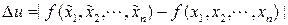
— модуль полного приращения функции.

Главной, т.е. линейной частью этого приращения, является, как известно, полный дифференциал du. Таким образом, имеем:

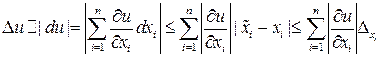
значит за границу абсолютной погрешности результата приближенно может быть принята величина

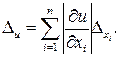(1.1)

Отсюда легко получается формула приближенной оценки относительной погрешности значения u,

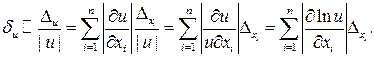
При больших количествах однотипных вычислений вступают в силу уже вероятностные, или статистические, законы формирования погрешностей результатов действий. Например, методами теории вероятностей показывается, что математическое ожидание абсолютной погрешности суммы п слагаемых с одинаковым уровнем абсолютных погрешностей, при достаточно большом n, пропорционально 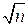. В частности, если n>10 и все слагаемые округлены до m-го десятичного разряда, то для подсчета абсолютной погрешности суммы S применяют правило Чеботарева: