Краткие теоретические сведения. Циклические коды названы так потому, что в них часть комбинаций кода либо все

Циклические коды названы так потому, что в них часть комбинаций кода либо все комбинации могут быть получены путём циклического сдвига одной или нескольких комбинаций кода. Циклический сдвиг осуществляется справа налево, причём крайний левый символ каждый раз переносится в конец комбинации. Практически все циклические коды относятся к систематическим кодам – в них контрольные и информационные разряды расположены на строго определённых местах. Кроме того, циклические коды относятся к числу блочных кодов. Каждый блок (одна буква является частным случаем блока) кодируется самостоятельно. Идея построения циклических кодов базируется на использовании неприводимых в поле двоичных чисел многочленов. Неприводимые многочлены – это такие многочлены, которые делятся без остатка только на себя и на единицу. Список неприводимых многочленов до шестнадцатого порядка включительно можно найти в книге: Цимбал В.П. "Задачник по теории информации и кодированию". Там же можно найти подробное описание методики по выбору соответствующего неприводимого многочлена.

Заданными величинами при кодировании являются число ошибок s, которое следует исправить, и общее число символов, посылаемых в линию, то есть длина слова n. Число информационных символов k и контрольных символов m, а также состав контрольных символов подлежат определению.

Кодирование

Для кодирования кодовой комбинации U(x) осуществляется следующая последовательность действий:

1) определяется кодовое расстояние: d_min = 2s + 1;

2) определяется число контрольных разрядов: r = log₂(n - 1);

3) определяется образующий многочлен P(x): его следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов r, а число ненулевых членов – не меньше d_min;

4) добавляется к исходному сообщению столько нулей, сколько будет контрольных разрядов (эта операция эквивалентна U(x) · 2^r);

5) находится значение корректирующих разрядов по остатку R(x) от деления комбинации U(x) · 2^r на образующий многочлен P(x);

6) находится закодированная комбинация F(x) следующим образом:

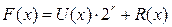Краткие теоретические сведения. Циклические коды названы так потому, что в них часть комбинаций кода либо все - student2.ru . (16)

Декодирование и исправление ошибок

Очевидно, что закодированная комбинация F(x) делится на P(x) без остатка. На этом и основана проверка кодовой комбинации на наличие ошибок при приеме. Если принятая комбинация делится на P(x) без остатка, то считается, что она принята без ошибок. Если же остаток, называемый синдромом, не равен нулю, то в принятой комбинации имеется ошибка. Обнаружение и исправление ошибок происходит по остаткам от деления принятой комбинации F(x) на образующий многочлен P(x). Следует отметить, что остаток от деления свидетельствует об ошибке, и неявно указывает, какой именно. Иными словами, каждый возможный остаток однозначно соответствует одному вектору ошибки (если число ошибок не превышает s).

Для исправления ошибки осуществляется следующая последовательность действий:

1) принятая комбинация делится на образующий многочлен;

2) если вес остатка (количество единиц) меньше или равен допустимому числу исправляемых ошибок s, необходимо перейти к пункту 5, если же больше, к пункту 3;

3) производится циклический сдвиг принятой комбинации на один разряд;

4) повторяются пункты 1-3 до тех пор, пока вес остатка не станет меньше или равен допустимому числу исправляемых ошибок;

5) принятая комбинация складывается по модулю 2 с остатком;

6) производится циклический сдвиг вправо на столько разрядов, на сколько была сдвинута суммируемая с последним остатком комбинация относительно принятой. В результате получается исправленная комбинация.

Кодирование

Кодовая комбинация, которую необходимо закодировать:

Краткие теоретические сведения. Циклические коды названы так потому, что в них часть комбинаций кода либо все - student2.ru .

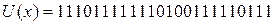Минимальное кодовое расстояние нашего кода: d_min = 3. Тогда по формуле (9) количество ошибок, которые мы можем исправить: s = (d_min ‑ 1)/2 = (3 – 1)/2 = 1. Число информационных символов: k = 24, число контрольных символов: r = 5, общее число символов, посылаемых в линию: n = 31(2 нуля допишем в начало).

Выбираем из таблицы полином 5-ой степени с 3-мя ненулевыми элементами:

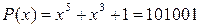Добавляем к исходному сообщению 5 нулей и получаем:

11101111 11101001 11110111 00000.

Далее находим значение корректирующих разрядов по результату от деления кодовой комбинации U(x) · 2⁵ на образующий многочлен P(x):

11101111111010011111011100000 | 101001

101001 |

101001

Следовательно, остаток от деления:

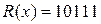Прибавляем к нашей комбинации с пятью нулями полученный остаток от деления, слева дописываем два нуля и получаем закодированное сообщение:

11101111 11101001 11110111 10111.

Декодирование

Пускай при передаче закодированного сообщения произошла ошибка в 3-м и декодер получил следующую искаженную кодовую комбинацию:

00 01101111 11101001 11110111 10111.

Пропуская несколько итераций, сделаем циклический сдвиг влево на 3 разряда и поделим получившуюся кодовую комбинацию (01101111111010011111011110111000) на образующий многочлен.

1101111111010011111011110111000 | 101001

101001 |

101001

Вес полученного остатка w = 1, что равно числу исправляемых ошибок данного кода. Значит, выполняем сложение по модулю 2 этого остатка с комбинацией, для которой он был найден:

(+) 1

После этого выполняем обратный циклический сдвиг вправо на 3 элемента:

0011101111111010011111011110111.

Отбрасываем последние 5 проверочных разрядов и первые 2 дописанные разряда и получаем декодированное сообщение с исправленной ошибкой:

111011111110100111110111.

Код БЧХ