Анализ смешанной системы связи
Автор курсовой работы__________ _______ О.В.Малышева
Специальность 210406 Сети связи и системы коммутации
Обозначение курсовой работы КР-02069964-210406-24-11
Руководитель работы__________ ________В.С. Дубровин
Оценка___________
Саранск 2011










 ОГЛАВЛЕНИЕ
ОГЛАВЛЕНИЕ
1. Исходные предпосылки…………………….…………………………..…3
2. Задание……………………………………………………………………..5
3. Задание 1…………………………………………………………………...7
4. Задание 2……..……………………………………………………………13
5. Задание 3……………………………………………………………….….16
6. Задание 4 ……………………………………………………………….…18
7. Задание 5 ………………………………………………………………….26
8. Задание 6…………………………………………………………………..29
9. Задание 7…………………………………………………………………..31
10. Задание 8…………………………………………………………………..35
11. Задание 9…………………………………………………………………..37
12. Вывод……………………………………………………………………...41
13. Список используемой литературы……………………………………....42









 ИСХОДНЫЕ ПРЕДПОСЫЛКИ.
ИСХОДНЫЕ ПРЕДПОСЫЛКИ.
Непрерывное сообщение 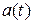 , наблюдаемое на выходе источника (ИС), представляет собой реализацию стационарного гауссовского случайного процесса с нулевым средним и известной функцией корреляции Ba(τ). Сообщение передается в цифровой форме по смешанной системе связи.
, наблюдаемое на выходе источника (ИС), представляет собой реализацию стационарного гауссовского случайного процесса с нулевым средним и известной функцией корреляции Ba(τ). Сообщение передается в цифровой форме по смешанной системе связи.
В передающем устройстве (ПДУ) системы на основе аналого-цифрового преобразования (АЦП) сообщение отображается в сигнал импульсно-кодовой модуляции (ИКМ), который модулирует один из информационных параметров гармонического переносчика. В результате формируется линейный сигнал 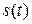 с дискретной амплитудной (ДАМ), дискретной частотной (ДЧМ) или дискретной относительной фазовой модуляции (ДОФМ).
с дискретной амплитудной (ДАМ), дискретной частотной (ДЧМ) или дискретной относительной фазовой модуляции (ДОФМ).
Сигнал дискретной модуляции передается по узкополосному гауссовскому непрерывному каналу связи (НКС).
В приемном устройстве (ПРУ) системы принятая смесь сигнала и шума 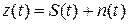 подвергается когерентной (КП) или некогерентной (НП) обработке с последующим поэлементным принятием решения методом однократного отсчета. Прием ДОФМ осуществляется либо методом сравнения фаз (СФ), либо методом сравнения полярностей (СП).
подвергается когерентной (КП) или некогерентной (НП) обработке с последующим поэлементным принятием решения методом однократного отсчета. Прием ДОФМ осуществляется либо методом сравнения фаз (СФ), либо методом сравнения полярностей (СП).
Восстановление оценки сообщения по принятому с искажениями сигналу ИКМ осуществляется на основе цифроаналогового преобразования (ЦАП) с последующей низкочастотной фильтрацией (ФНЧ).
Исходные данные приведены в таблице 1, где 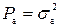 – мощность (дисперсия) сообщения, β – показатель затухания функции корреляции, L – число уровней квантования, G0 - постоянная энергетического спектра шума НКС, h2 – отношение сигнал-шум (ОСШ) по мощности на входе детектора, δдоп – допустимая относительная среднеквадратическая погрешность (СКП) восстановления сообщения, ОФМ –относительная фазовая модуляция, СП – сравнение полярностей.
– мощность (дисперсия) сообщения, β – показатель затухания функции корреляции, L – число уровней квантования, G0 - постоянная энергетического спектра шума НКС, h2 – отношение сигнал-шум (ОСШ) по мощности на входе детектора, δдоп – допустимая относительная среднеквадратическая погрешность (СКП) восстановления сообщения, ОФМ –относительная фазовая модуляция, СП – сравнение полярностей.









 Таблица 1 - Исходные данные для расчетов
Таблица 1 - Исходные данные для расчетов
| ИС; АЦП; L=8 | ПДУ | НКС | ПРУ | ЦАП; ПС | Функция корреляции сообщения Ba(τ), τ , мс | |||
| Pa, В2 |  , с-1 , с-1 | Способ передачи | Частота, МГц | G0, Вт×с | h2 | Способ приема | δдоп | |
| f0 | ||||||||
| ОФМ | 3,3 | 0,0023 | 6,4 | СП | 0,19 | 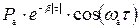 , , 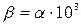 , с-1, , с-1, 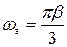 |









 ЗАДАНИЕ
ЗАДАНИЕ
1. Изобразить структурную схему смешанной системы связи и нарисовать сигналы в различных ее сечениях.
2. Рассчитать спектр плотности мощности сообщения Ga(ω)  ; энергетическую ширину спектра ∆ ω0; интервал корреляции τk сообщения. Построить графики Ba(τ) и Ga(ω).
; энергетическую ширину спектра ∆ ω0; интервал корреляции τk сообщения. Построить графики Ba(τ) и Ga(ω).
3. Рассчитать СКП фильтрации 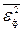 сообщения; мощность
сообщения; мощность 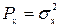 отклика ФНЧ; частоту fд и интервал T временной дискретизации отклика ФНЧ. Считать, что исходное сообщение воздействует на идеальный ФНЧ с частотой среза fср=∆fа= fв – fн = fв (fн=0).
отклика ФНЧ; частоту fд и интервал T временной дискретизации отклика ФНЧ. Считать, что исходное сообщение воздействует на идеальный ФНЧ с частотой среза fср=∆fа= fв – fн = fв (fн=0).
4. Рассчитать интервал квантования ∆q, пороги квантования hl, 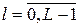 , и СКП квантования
, и СКП квантования 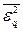 квантователя АЦП; распределение вероятностей Pl ,
квантователя АЦП; распределение вероятностей Pl , 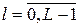 , и интегральное распределение вероятностей Fl,
, и интегральное распределение вероятностей Fl, 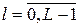 , квантованной последовательности
, квантованной последовательности 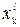 ; энтропию
; энтропию 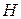 , производительность
, производительность 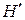 и избыточность
и избыточность 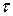 квантованной последовательности. В расчетах принять квантование с равномерным шагом.
квантованной последовательности. В расчетах принять квантование с равномерным шагом.
5. Закодировать L-ичную последовательность 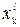 двоичным безызбыточным кодом
двоичным безызбыточным кодом 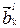 ; выписать все кодовые комбинации кода и построить таблицу кодовых расстояний
; выписать все кодовые комбинации кода и построить таблицу кодовых расстояний 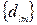 кода. Рассчитать априорные вероятности P(0) и P(1) передачи нуля и единицы по двоичному дискретному каналу связи (ДКС); ширину спектра сигнала
кода. Рассчитать априорные вероятности P(0) и P(1) передачи нуля и единицы по двоичному дискретному каналу связи (ДКС); ширину спектра сигнала 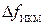 сигнала ИКМ.
сигнала ИКМ.
6. Рассчитать и построить спектр сигнала дискретной модуляции и определить ширину спектра 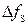 .
.
7. 



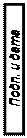





 Рассчитать приходящуюся в среднем на один двоичный символ (бит) мощность
Рассчитать приходящуюся в среднем на один двоичный символ (бит) мощность 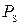 и амплитуду
и амплитуду 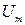 сигнала дискретной модуляции, необходимую для обеспечения требуемого ОСШ
сигнала дискретной модуляции, необходимую для обеспечения требуемого ОСШ 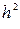 ; пропускную способность С гауссовского НКС. Построить функции плотности вероятности (ФПВ) мгновенных значений и огибающей узкополосной гауссовской помехи (УГП), а также ФПВ мгновенных значений и огибающей суммы гармонического сигнала и УГП.
; пропускную способность С гауссовского НКС. Построить функции плотности вероятности (ФПВ) мгновенных значений и огибающей узкополосной гауссовской помехи (УГП), а также ФПВ мгновенных значений и огибающей суммы гармонического сигнала и УГП.
8. Изобразить схему приемника сигнала дискретной модуляции. Рассчитать среднюю вероятность ошибки 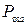 и скорость
и скорость 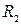 передачи информации по двоичному симметричному ДКС; показатель эффективности Э передачи сигнала дискретной модуляции по НКС.
передачи информации по двоичному симметричному ДКС; показатель эффективности Э передачи сигнала дискретной модуляции по НКС.
9. Рассчитать скорость передачи информации 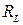 по L-ичному ДКС и относительные потери в скорости передачи информации; СКП шума передачи
по L-ичному ДКС и относительные потери в скорости передачи информации; СКП шума передачи 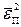 и относительную суммарную СКП
и относительную суммарную СКП 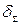 восстановленного непрерывного сообщения. Указать пути уменьшения величины
восстановленного непрерывного сообщения. Указать пути уменьшения величины 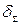 , если окажется, что
, если окажется, что 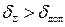 .
.



















 ЗАДАНИЕ 1.
ЗАДАНИЕ 1.
Изобразить структурную схему смешанной системы связи и нарисовать сигналы в различных ее сечениях.
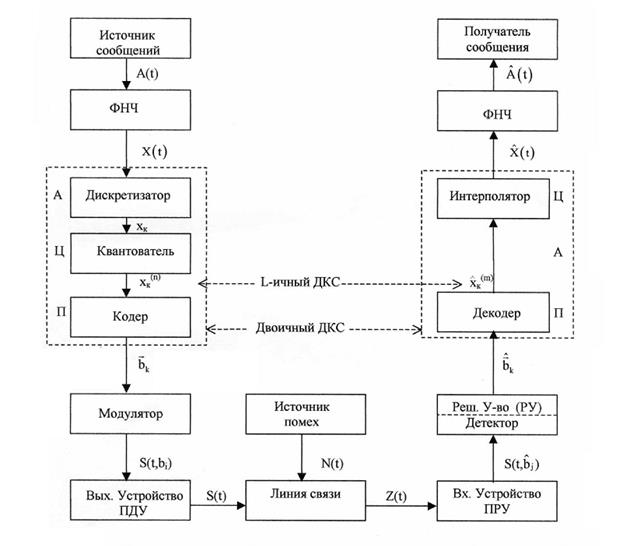
Рис. 1. Структурная схема смешанной системы связи.
На практике нередко встает проблема передачи непрерывного сообщения по дискретному каналу связи. Эта проблема решается при использовании передачи непрерывного сообщения методом импульсно-кодовой модуляции (ИКМ). Структурная схема передачи непрерывного сообщения методом ИКМ приведена на рис.1. Она состоит из источника сообщения (ИС), двоичного дискретного канала связи (ДКС), составной частью которого является непрерывный канал связи (НКС), цифро-аналогового преобразователя (ЦАП) и получателя сообщения (ПС). Каждая из указанных частей системы содержит еще целый ряд элементов.








 Источник сообщения – это некоторый объект или система, информацию о состоянии или поведении которого необходимо передать на некоторое расстояние. Причем под объектом или системой подразумевают человека, ЭВМ, автоматическое устройство или что-либо другое. Передаваемая от ИС информация является непрерывной для получателя. Поэтому количественную меру передаваемой по системе информации в теории электросвязи выражают через статистические (вероятностные) характеристики сообщений (сигналов). Сообщение есть физическая форма представления информации. Часто сообщение представляют в виде изменяющегося во времени тока или напряжения, отображающих передаваемую информацию. Например, в телефонии это изменение тока микрофона под действием звукового давления говорящего человека, в телевидении это изменение напряжения на выходе видикона под действием изменения яркости или цветности отображаемого объекта и т.д.
Источник сообщения – это некоторый объект или система, информацию о состоянии или поведении которого необходимо передать на некоторое расстояние. Причем под объектом или системой подразумевают человека, ЭВМ, автоматическое устройство или что-либо другое. Передаваемая от ИС информация является непрерывной для получателя. Поэтому количественную меру передаваемой по системе информации в теории электросвязи выражают через статистические (вероятностные) характеристики сообщений (сигналов). Сообщение есть физическая форма представления информации. Часто сообщение представляют в виде изменяющегося во времени тока или напряжения, отображающих передаваемую информацию. Например, в телефонии это изменение тока микрофона под действием звукового давления говорящего человека, в телевидении это изменение напряжения на выходе видикона под действием изменения яркости или цветности отображаемого объекта и т.д.
 |
Сигнал на входе АЦП представлен на рисунке 2:
Рис. 2. Сигнал на входе АЦП.
В ПДУ сообщение сначала фильтруется с целью ограничения его спектра некоторой верхней частотой fв. Это необходимо для эффективного представления отклика ФНЧ x(t) в виде последовательности отсчетов наблюдаемых на выходе дискретизатора. Отметим, что фильтрация связана с
внесением погрешности εф(t) , отображающей ту часть сообщения, которая подавляется ФНЧ. Далее отчеты хk квантуются по уровню. Процесс квантования связан с нелинейным преобразованием непрерывнозначных отсчетов {хk} в дискретнозначные { 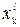 } l=
} l= 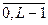 что также привносит погрешность, называемую шумом квантования εq(t) . Квантованные уровни {
что также привносит погрешность, называемую шумом квантования εq(t) . Квантованные уровни { 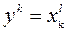 } затем кодируются двоичным безызбыточным кодом.
} затем кодируются двоичным безызбыточным кодом.
Сигнал на выходе дискретизатора представлен на рисунке 3:
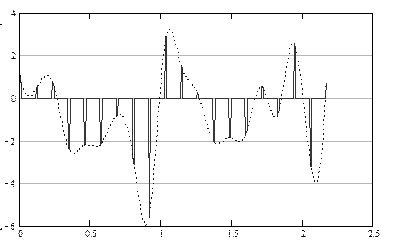 |




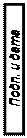





 Рис. 3. Сигнал на выходе дискретизатора.
Рис. 3. Сигнал на выходе дискретизатора.
Сигнал на выходе квантователя представлен на рисунке4:
 |
Рис. 4. Сигнал на выходе квантователя.









 Сигнал на выходе АЦП представлен на рисунке 5:
Сигнал на выходе АЦП представлен на рисунке 5:
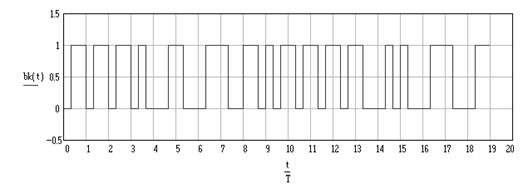
Рис. 5. Сигнал на выходе АЦП.
Последовательность кодовых комбинаций 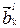 образует сигнал ИКМ, который подводится к модулятору – устройству, предназначенному для согласования источника сообщений с используемой линией связи. Модулятор формирует линейный сигнал S(t,bi) , который представляет собой электрическое или электромагнитное колебание, способное распространяться по линии связи и однозначно связанное с передаваемым сообщением (в данном случае с сигналом ИКМ). Сигнал S(t,bi) создается в результате модуляции – процесса изменения одного или нескольких параметров переносчика по закону модулирующего ИКМ сигнала. При использовании гармонического переносчика
образует сигнал ИКМ, который подводится к модулятору – устройству, предназначенному для согласования источника сообщений с используемой линией связи. Модулятор формирует линейный сигнал S(t,bi) , который представляет собой электрическое или электромагнитное колебание, способное распространяться по линии связи и однозначно связанное с передаваемым сообщением (в данном случае с сигналом ИКМ). Сигнал S(t,bi) создается в результате модуляции – процесса изменения одного или нескольких параметров переносчика по закону модулирующего ИКМ сигнала. При использовании гармонического переносчика
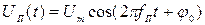 различают сигналы амплитудной, частотной и фазовой модуляции (АМ, ЧМ и ФМ).
различают сигналы амплитудной, частотной и фазовой модуляции (АМ, ЧМ и ФМ).
Для предотвращения внеполосных излучений в одноканальной системе или при организации многоканальной связи, а также для установления требуемого отношения сигнал-шум (ОСШ) на входе приемника канальный сигнал фильтруется и усиливается в выходных каскадах ПДУ. Сигнал S(t) с выхода ПДУ поступает в линию связи, где на него накладывается помеха n(t). На вход ПРУ воздействует смесь z(t)=S(t)+n(t) переданного сигнала и помехи. Здесь на входных каскадах ПРУ принятый сигнал фильтруется и подается на детектор. При демодуляции из принятого сигнала 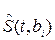 выделяется закон изменения информационного параметра, который в нашем случае пропорционален сигналу ИКМ. При этом для опознания переданных двоичных символов на выход демодулятора подключается решающее устройство (РУ). При передаче двоичных сигналов
выделяется закон изменения информационного параметра, который в нашем случае пропорционален сигналу ИКМ. При этом для опознания переданных двоичных символов на выход демодулятора подключается решающее устройство (РУ). При передаче двоичных сигналов 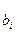 , i=0, 1, по ДКС наличие помех в НКС приводит к неоднозначным решениям (ошибкам) РУ, что, в свою очередь, вызывает несоответствие переданных
, i=0, 1, по ДКС наличие помех в НКС приводит к неоднозначным решениям (ошибкам) РУ, что, в свою очередь, вызывает несоответствие переданных 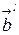 и принятых
и принятых 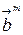 кодовых комбинаций. Наконец, для восстановления переданного сообщения a(t) т.е. получения оценки
кодовых комбинаций. Наконец, для восстановления переданного сообщения a(t) т.е. получения оценки 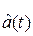 , принятые кодовые комбинации подвергаются декодированию, интерполяции и низкочастотной фильтрации. При этом в декодере по двоичным кодовым комбинациям восстанавливаются L-ичные уровни
, принятые кодовые комбинации подвергаются декодированию, интерполяции и низкочастотной фильтрации. При этом в декодере по двоичным кодовым комбинациям восстанавливаются L-ичные уровни 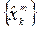 ,
, 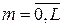 .
. 








Сигнал на выходе декодера представлен на рисунке 6:
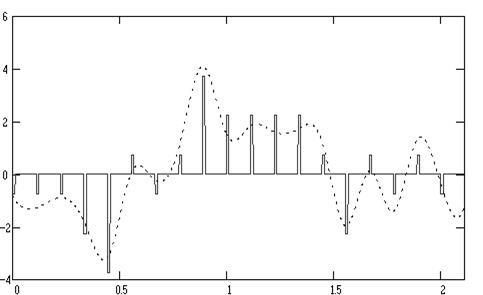
Рис. 6. Сигнал на выходе декодера.




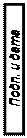





 Сигнал на выходе интерполятора ЦАП представлен на рисунке 7:
Сигнал на выходе интерполятора ЦАП представлен на рисунке 7:
Рис. 7. Сигнал на выходе интерполятора ЦАП.
Наличие ошибок в двоичном ДКС приводит к ошибкам передачи в L-ичном ДКС и, соответственно к возникновению шума передачи 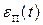 . Совокупное действие погрешности фильтрации, шумов квантования и передачи приводит к неоднозначности между переданными и принятыми сообщениями
. Совокупное действие погрешности фильтрации, шумов квантования и передачи приводит к неоднозначности между переданными и принятыми сообщениями 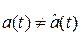
В системах передачи непрерывных сообщений верность (качество) передачи считается удовлетворительным, если минимальная суммарная относительная СКП восстановления не превосходит допустимую, т.е. 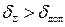 .
.









 ЗАДАНИЕ 2.
ЗАДАНИЕ 2.
Рассчитать спектр плотности мощности сообщения Ga(ω); энергетическую ширину спектра ∆ ω0; интервал корреляции τk сообщения. Построить графики Ba(τ) и Ga(ω).
Во временной и спектральной областях стационарный случайный процесс определяется функцией корреляции Ba(τ) и спектром плотности мощности Ga(ω).
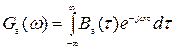 ; (1)
; (1)
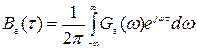 . (2)
. (2)
Учитывая, что для стационарного случайного процесса эти функции действительные и четные, то Ba(τ) и Ga(ω) можно представить в следующем виде:
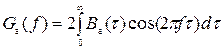 ; (3)
; (3)
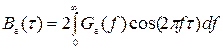 . (4)
. (4)
Рассчитаем энергетический спектр или спектр плотности мощности, используя его функцию корреляции. В виду того, что область интегрирования положительна можно опустить знак модуля в выражении для функции корреляции.
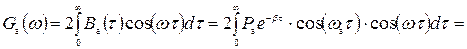
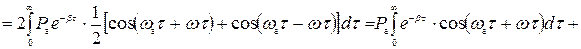
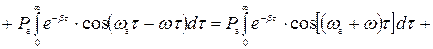
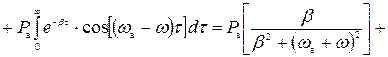










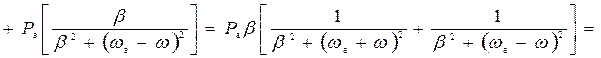
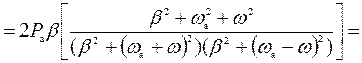
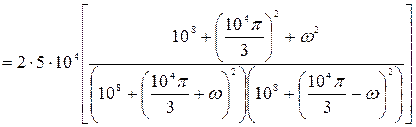 ; (5)
; (5)
Теперь по известным функциям Ba(τ) и Ga(ω) можно найти такие параметры как энергетическую ширину спектра ∆ ω0 и интервал корреляции τk.
Рассчитаем интервал корреляции.
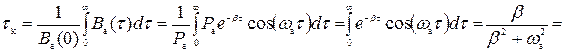
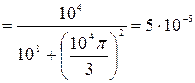 [с]. (6)
[с]. (6)
Найдем начальную энергетическую ширину спектра сообщения.
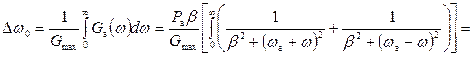
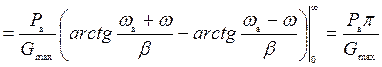 . (7)
. (7)









 Для нахождения Gmaxвозьмем производную Ga(ω) и приравняем ее к нулю.
Для нахождения Gmaxвозьмем производную Ga(ω) и приравняем ее к нулю.
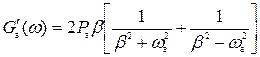 . (8)
. (8)
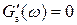 при
при 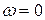 , значит, следовательно, Gmax при
, значит, следовательно, Gmax при 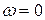 :
:











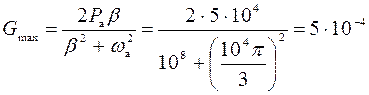 [
[ 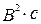 ]. (9)
]. (9)
Подставляя 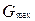 в выражение(7) получаем
в выражение(7) получаем
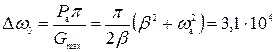
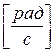 . (10)
. (10)
Графики функции корреляции и спектра плотности мощности представлены на рис.8 и рис.9 соответственно.
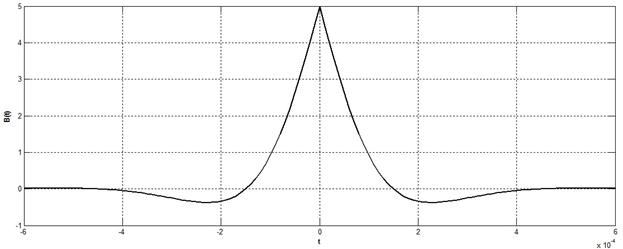
Рис. 8. График функции корреляции - Ba(τ).










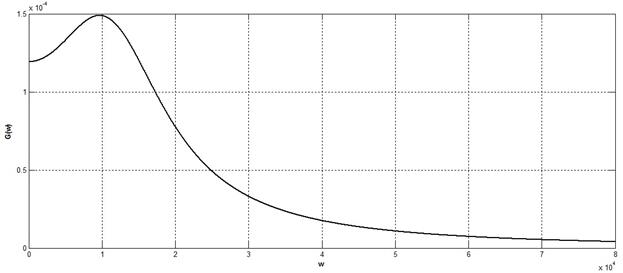
Рис. 9. График спектра плотности мощности - Ga(τ).









 ЗАДАНИЕ 3.
ЗАДАНИЕ 3.
Рассчитать СКП фильтрации 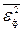 сообщения; мощность
сообщения; мощность 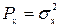 отклика ФНЧ; частоту fд и интервал T временной дискретизации отклика ФНЧ. Считать, что исходное сообщение воздействует на идеальный ФНЧ с частотой среза fср=∆fа= fв – fн = fв (fн=0).
отклика ФНЧ; частоту fд и интервал T временной дискретизации отклика ФНЧ. Считать, что исходное сообщение воздействует на идеальный ФНЧ с частотой среза fср=∆fа= fв – fн = fв (fн=0).
Отклик ФНЧ на гауссовское воздействие будет случайным процессом с нулевым математическим ожиданием и мощностью, определяемой из соотношения:
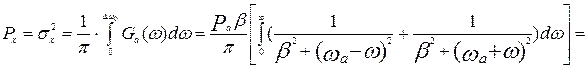
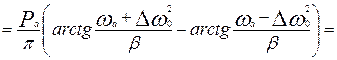
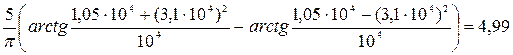
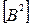 . (11)
. (11)
Здесь учтено, что амплитудно-частотная характеристика идеального ФНЧ равна единице в полосе частот 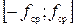 и нулю вне этой полосы. Кроме того, его полоса пропускания
и нулю вне этой полосы. Кроме того, его полоса пропускания 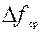 принята равной энергетической ширине спектра: ∆fср=∆fа= fв – fн, где fн и fв – соответственно нижняя и верхняя частоты, которые равны: fн =0, fв >0. Отсюда частота среза ФНЧ fср = fв. Это говорит о том, что отклик ФНЧ является ограниченным по спектру сообщением. В нем не содержатся составляющие исходного сообщения на частотах f > fв.
принята равной энергетической ширине спектра: ∆fср=∆fа= fв – fн, где fн и fв – соответственно нижняя и верхняя частоты, которые равны: fн =0, fв >0. Отсюда частота среза ФНЧ fср = fв. Это говорит о том, что отклик ФНЧ является ограниченным по спектру сообщением. В нем не содержатся составляющие исходного сообщения на частотах f > fв.
Количественно потери при фильтрации сообщения характеризуются средней квадратической погрешностью:
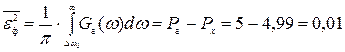
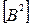 . (12)
. (12)
Найдем частоту и интервал временной дискретизации отклика ФНЧ.









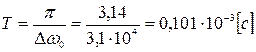 . (13)
. (13)
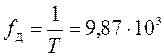 [кГц]. (14)
[кГц]. (14)
ЗАДАНИЕ 4.
Рассчитать интервал квантования ∆q, пороги квантования hl, 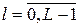 , и СКП квантования
, и СКП квантования 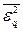 квантователя АЦП; распределение вероятностей Pl ,
квантователя АЦП; распределение вероятностей Pl , 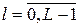 , и интегральное распределение вероятностей Fl,
, и интегральное распределение вероятностей Fl, 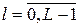 , квантованной последовательности
, квантованной последовательности 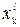 ; энтропию
; энтропию 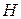 , производительность
, производительность 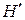 и избыточность
и избыточность 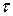 квантованной последовательности. В расчетах принять квантование с равномерным шагом.
квантованной последовательности. В расчетах принять квантование с равномерным шагом.
Импульсы на выходе дискретизатора могут принимать бесчисленное множество значений из ограниченного или неограниченного диапазона 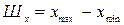 , называемого шкалой сообщения. В результате равномерного квантования с шагом
, называемого шкалой сообщения. В результате равномерного квантования с шагом 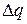 этот диапазон разбивается на конечное число уровней квантования
этот диапазон разбивается на конечное число уровней квантования 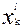 ,
, 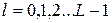 .
.
Для определенного шага квантования 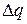 порогов квантования учтем, что с вероятностью 0,997 гауссовский случайный процесс находится в диапазоне
порогов квантования учтем, что с вероятностью 0,997 гауссовский случайный процесс находится в диапазоне 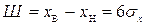 , где
, где 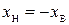 (ввиду симметрии ФПВ).
(ввиду симметрии ФПВ).
Если в этом диапазоне разместить L-2 уровня, а два уровня отвести на области вне этого диапазона, т.е. 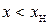 и
и 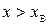 , то шаг квантования можно рассчитать следующим образом:
, то шаг квантования можно рассчитать следующим образом:
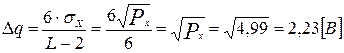 . (15)
. (15)
Пороги квантования находим из выражения:
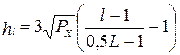 , где
, где 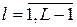 ; (16)
; (16)
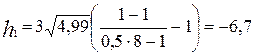 ;
;




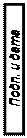






 ;
;




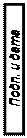






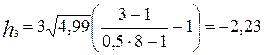 ;
;
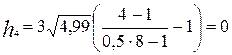 ;
;
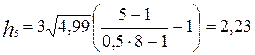 ;
;
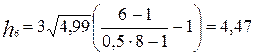 ;
;
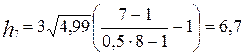 .
.
Таблица 2 - Пороги квантования.
 | |||||||||
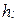 ,В ,В | 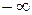 | -6,7 | -4,47 | -2,23 | 2,23 | 4,47 | 6,7 | 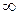 |
Уровни квантования определяются следующим образом:
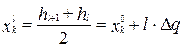 , (17)
, (17)
где 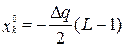 ,
, 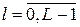 . (18)
. (18)
Из формулы (18) находим:
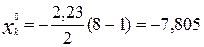 .
.
