Дискретно-стохастические модели

Как следует из названия, данный вид моделей ориентирован на описание систем, которые проявляют статистически закономерное случайное поведение, а время в них можно рассматривать как дискретную величину. Сущность дискретизации времени такая же, как и в дискретно-детерминированных моделях. Модели систем такого рода могут быть построены на основе двух схем формализованного описания. Во-первых, это конечно-разностные уравнения, среди переменных которых используют функции, задающие случайные процессы. Во-вторых, в них применяют вероятностные автоматы [12].

Пример построения дискретно-стохастической системы.Пусть имеется некоторая производственная система, структура которой изображена на рис. 3.8. В рамках этой системы перемещается однородный материальный поток, проходящий стадии складирования и производства.

Пусть, например, поток сырья состоит из металлических болванок, которые складируются на входном складе. Затем эти болванки поступают на производство, где из них производят какое-то изделие. Готовые изделия складируются на выходном складе, откуда их забирают для дальнейших действий с ними (передают на следующие фазы производства или на реализацию). В общем случае такая производственная система преобразует материальные потоки сырья, материалов и полуфабрикатов в поток готовой продукции.

Пусть шаг изменения времени в данной производственной системе будет равен единице (Д?= 1). За единицу мы примем смену работы этой системы. Будем считать, что процесс изготовления изделия длится один временной шаг.

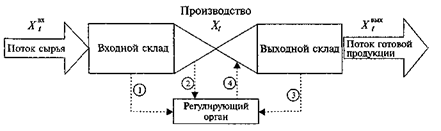
Рис. 3.8, Схема производственной системы

Управление производственным процессом осуществляется специальным регулирующим органом, которому задан план выпуска изделий в виде директивной интенсивности выпуска продукции (количество изделий, которое необходимо изготовить за единицу времени, в данном случае за смену). Обозначим эту интенсивность d_t. Фактически это скорость выпуска продукции. Пусть d_t=а+ bt, т. е. является линейной функцией. Это означает, что с каждой последующей сменой план увеличивается на величину bt.

Поскольку мы имеем дело с однородным материальным потоком, то считаем, что в среднем объем сырья, приходящего в систему в единицу времени, объем производства в единицу времени, объем готовой продукции, уходящей в единицу времени из системы, должны быть равны d_t.

Входной и выходной потоки для регулирующего органа неуправляемы, их интенсивность (или скорость — число болванок либо изделий в единицу времени, соответственно приходящих в систему и уходящих из нее) должны быть равны d_t. Однако в процессе транспортировки болванки могут быть утеряны, или часть из них будет некачественной, или по каким-то причинам их поступит больше, чем нужно, и т.п. Поэтому будем считать, что входной поток обладает интенсивностью:

х_t^вх =d_t+ξ_t^вх,

где ξ₁^вх — равномерно распределенная случайная величина от —15 до +15.

Примерно те же самые процессы могут происходить с выходным потоком. Поэтому выходной поток обладает следующей интенсивностью:

х_t^вых =d_t+ξ_t^вых,

где ξ_t^вых — нормально распределенная случайная величина с нулевым математическим ожиданием и дисперсией, равной 15.

Будем считать, что и в процессе производства имеются случайности, связанные с неявкой рабочих на работу, поломкой станков и т.п. Описывает эти случайности нормально распределенная случайная величина с нулевым математическим ожиданием и дисперсией, равной 15. Обозначим ее ξ_t/Процесс производства длится единицу времени, за которую с входного склада изымается x_t сырья, затем это сырье обрабатывается и передается на выходной склад за ту же единицу времени. Регулирующий орган получает информацию о работе системы тремя возможными способами (они отмечены цифрами 1, 2, 3 на рис. 3.8). Мы считаем, что эти способы получения информации по каким-либо причинам являются в системе взаимоисключающими.

Способ 1.Регулирующий орган получает только информацию о состоянии входного склада (например, об изменении запасов на складе либо об отклонении объема запасов от их нормативного уровня) и по ней судит о скорости протекания производственного процесса (о скорости изымания сырья со склада):

1) (u_t^вх- u_t-1^вх )— изменение объема запасов на складе (u_t^вх — объем сырья на входном складе в момент времени t);

2) (ù- u_t^вх ) — отклонение объема сырья на входном складе от нормы запасов.

Способ2. Регулирующий орган получает информацию непосредственно с производства (x_t — фактическая интенсивность производства) и сравнивает ее с директивной интенсивностью (d_t-x_t).

Способ 3.Регулирующий орган получает информацию, как и при способе 1, но с выходного склада в виде (u_t^вых- u_t-1^вых )— или (ù -u_t^вых ). Он также судит о производственном процессе на основания косвенных данных — росте или уменьшении запасов готовой продукции.

Чтобы поддержать заданную интенсивность выпуска продукции d_t, регулирующий орган принимает решения y_t, (либо ( y_t - y_t-₁)), нацеленные на изменение фактической интенсивности выпуска x_t. В качестве решения регулирующий орган сообщает производству значения интенсивности, с которой надо работать, т. е. x_t = y_t. Второй вариант управляющего решения — (y_t-y_t-1), т.е. регулирующий орган сообщает производству, на сколько нужно увеличить или уменьшить интенсивность производства (х_t-х_t-1).

В зависимости от способа получения информации и вида переменной, описывающей управляющее воздействие, на принятие решений могут влиять следующие величины.

1. База решения (величина, которой должна быть равна фактическая интенсивность производства, если бы не было отклонений):

директивная интенсивность выпуска в момент t(d_t);

темп изменения директивной интенсивности выпуска в момент t(d_t-d_t-1).

2. Величина отклонения:

отклонение фактического выпуска от директивного (d_t-x_t);

отклонение фактического объема выпуска от планового объема

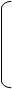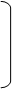t t

Σd _τ - Σх _τ

τ=0 τ=0

изменение уровня запасов на входном ((u_t^вх- u_t-1^вх) или выходном

(u_t^вых- u_t-1^вых) складах;

отклонение уровня запасов на входном (ù- u_t^вх) или выходном (ù -u_t^вых) складах от нормативного уровня.

В общем случае управленческое решение, принимаемое регулирующим органом, состоит из следующих составляющих:

Примеры решений:

y_t = d_t+y(d_t-1-x_t-1);

y_t = d_t-y(ù -u_t^вых)

Принимая различные по форме решения, регулирующий орган стремится достичь главную цель — приблизить фактическую интенсивность выпуска к директивной. Однако он не всегда может непосредственно ориентироваться в своих решениях на степень достижения этой цели (d_t — x_t). Конечные результаты могут выражаться в достижении локальных целей — стабилизации уровня запасов на входном или выходном складе (и_t ^вх(вых)- и_{t -1}^вх(вых)) либо в приближении уровня запасов на складе к нормативному (и - и ^вх(^вых)). В зависимости от достигаемой цели в управляющем решении определяется вид знака (+ или -) перед долей рассогласования, используемой для регулирования.

Пусть в нашем случае регулирующий орган получает информацию о состоянии входного склада (изменение уровня запасов). Известно, что в любой системе управления имеют место запаздывания по выработке и реализации решения. В данном примере информация о состоянии входного склада поступает в орган регулирования с запаздыванием на один временной шаг. Такое запаздывание называется запаздыванием по выработке решения и означает, что к моменту получения информации в регулирующем органе реальное состояние уровня запасов на входном складе будет уже другим. После того как регулирующий орган принял решение у_t также потребуется время (в нашем примере это будет единица времени) для доведения решения до исполнителя. Значит, фактическая интенсивность производства равна не y_t, а тому решению, которое управляющий орган принял единицу времени назад. Это — запаздывание по реализации решения.

Для описания нашей производственной системы имеем следующие уравнения:

x_t ^BX =d_t+ ξ_t^вх

x_t ^вых = d_t +ξ_t^вых;

y_t= d_t + y(u -u_t-2^вх)

x_t = y_t-1+ξ_t

u_t^вх - u_t-1^вх = x_t ^вх - x_t

Данная система уравнений позволяет построить модель производственной системы, в которой входными переменными будут d_t, ξ_t^вх, ξ_t^вых, ξ_t,а

выходной — x_t . Это так, поскольку внешний наблюдатель рассматривает наше производство как систему, получающую сырье с интенсивностью d_t и производящую продукцию с интенсивностью x_t, подвергаясь случайностям ξ_t^вх, ξ_t^вых, ξ_{t .}Осуществив все подстановки в полученной системе уравнений, приходим к одному уравнению динамики, характеризующему поведение x_t в зависимости от d_t, ξ_t^вх, ξ_t^вых, ξ_t.

Рассмотренная выше модель не содержала ограничений на объемы складов и мощности производства. Если принять, что емкость входного склада равна V^вх, емкость выходного склада — V^BX, a мощность производства — М, то новая система уравнений для такой нелинейной производственной системы будет следующей:

x_t ^BX =min((d_t + ξ_t^вх ),(V^вх - u_t^вх )) — нельзя на входной склад положить больше, чем позволит место;

x ^вых =min((d_t + ξ_t^вых),(V^вых -u_t^вых)) — нельзя взять с выходного склада больше изделий, чем там имеется;

y_t=d_t+ y(u_t^вх -u_t-1^вх)

x_t ^BX = min((u_t^вх, (y_t-1+ ξ_t^вх), М, (V^вых - u_t^вых )) - нельзя произвести больше изделий, чем приказано, ограничивающими факторами являются число имеющихся заготовок и наличие свободного места на выходном складе;

u_t^вх -u_t-1^вх = x_t ^BX - x_t