Алгоритм метода обратного переменного шага
Начальный этап. Выбрать начальную точку x1 и приращение Dx. Задать коэффициенты деформации шага a > 1, 0<b < 1 и точность поиска e>0. Положить k = 1 и перейти к основному этапу.
Основной этап. Шаг 1. Если Dx < e то остановиться; точкой минимума является точка xk, иначе вычислить xk+1 = xk+Dx и перейти к шагу 2.
Шаг 2. Если f(xk) > f(хk+1), то Dх=a Dx. В противном случае положить Dx =-bDx. Заменить k = k + 1 и перейти к шагу 1.
Пример расчета экстремума функции методом обратного переменного шага.
Постановка задачи. Рассчитать минимум функции f(x) = x2 – 10х+3с точностью e=0,1. Начальную точку принять равной x1=-1.
Выбираем следующие параметры метода: начальный шаг - Dх=1, коэффициенты растяжения и сжатия шага - a =1,5; b=0,4. Результаты расчета представлены в таблице 2.6.
Таблица 2.6
Расчет минимума функции f(x) = x2 – 10х+3методом обратного переменного шага.
| № | xk | Δx | f(xk) | Критерий |
| -1.000 | 1.000 | 14.000 | не достигнут | |
| 0.000 | 1.500 | 3.000 | не достигнут | |
| 1.500 | 2.250 | -9.750 | не достигнут | |
| 3.750 | 3.375 | -20.438 | не достигнут | |
| 7.125 | -1.350 | -17.484 | не достигнут | |
| 5.775 | -2.025 | -21.399 | не достигнут | |
| 3.750 | 0.810 | -20.438 | не достигнут | |
| 4.560 | 1.215 | -21.806 | не достигнут | |
| 5.775 | -0.486 | -21.399 | не достигнут | |
| 5.289 | -0.729 | -21.916 | не достигнут | |
| 4.560 | 0.292 | -21.806 | не достигнут | |
| 4.852 | 0.437 | -21.978 | не достигнут | |
| 5.289 | -0.175 | -21.916 | не достигнут | |
| 5.114 | -0.262 | -21.987 | не достигнут | |
| 4.852 | 0.105 | -21.978 | не достигнут | |
| 4.957 | 0.157 | -21.998 | не достигнут | |
| 5.114 | -0.063 | -21.987 | достигнут |
Таким образом, в результате реализации метода обратного переменного шага за шестнадцать итераций определена минимальная точка х*=5,114 с точностью 0,063.
2.2.2. Метод квадратичной аппроксимации.
Метод основан на предположении о том, что в ограниченном интервале можно аппроксимировать функцию квадратичным полиномом, который используется для оценивания координаты оптимума. Оценка оптимального значения рассчитывается по формуле:
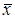= (x2 + x1)/2 - (a1/2a2).
Предполагается, что заданы x1, x2, x3, и известны значения функции в этих точках f1, f2, f3, а аппроксимирующая функция
g(x) = a0 + a1(x - x1) + a2(x - x1)(x - x2)
совпадает с f(x) в трех указанных точках.
Коэффициенты полинома определяются уравнениями
a0 = f1; a1 = (f2 - f1)/(x2 - x1); a2 = 1/(x3 - x2)×[(f3 - f1)/(x3 - x1) - (f2 - f1)(x2 - x1)].
Для унимодальных функций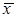 
оказывается приемлемой для оценки оптимума x*.
Алгоритм метода квадратичной аппроксимации.
Шаг 1. Задать x1, x2, x3, и вычислить значения функции в этих точках f(х1), f(х2), f(х3).
Шаг 2. Рассчитать a0 = f(х1); a1 = (f(х2) - f(х1))/(x2 - x1);
a2 = 1/(x3 - x2)×[(f(х3) - f(х1))/(x3 - x1) - (f(х2) - f(х1))(x2 - x1)].
Шаг 2. Вычислить оптимальное решение: 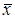= (x2 + x1)/2 - (a1/2a2).
Пример расчета экстремума функции методом квадратичной аппроксимации.
Постановка задачи.Найти минимум функции f(x) = x2 + 5x методом квадратичной аппроксимации.
Для реализации метода необходимо выбрать три точки, по который будет производиться аппроксимация. Задаем следующие значения: x1=-5, x2=0, x3=5, Результаты расчета, реализованного средствами ECXEL, представлены в таблице 2.7
Таблица 2.7
Расчет экстремума функции f(x) = x2 + 5x методом квадратичной аппроксимации
| x1 | x2 | x3 | f(x1) | f(x2) | f(x3) | a0 | a1 | a2 | xопт |
| -5,00 | 0,00 | 5,00 | 0,00 | 0,00 | 50,00 | 0,00 | 0,00 | 3,00 | -2,50 |
Таким образом, с использованием метода квадратичной аппроксимации за одну итерацию найдена точка минимума xопт=-2,5, которая совпадает с точкой экстремума x*=-2,5, полученной аналитически.
2.2.3. Метод Пауэлла.
Заключается в последовательном применении процедуры оценивания с использованием квадратичной аппроксимации. Схему алгоритма можно описать следующим образом.