Смысловой подход к измерению количества информации
В рамках смыслового выделяют семантический и прагматический подходы.
При семантическом подходе пытаются измерить смысловое содержание сообщений.
Пусть поступили два сообщения:
Дважды два - четыре.
Совершенно незнакомая математическая формула.
Первое сообщение можно выразить словами «известно все», а второе - «неизвестно ничего». С одной стороны эти сообщения являются противоположными. Однако в них есть и что-то общее. Обшее заключается в том, что после их получения наши знания не изменились. Информация была передана, мы ее получили, но обнаружить ее невозможно.
Таким образом, при семантическом подходе, количество полученной информации предлагается измерять степенью изменения знаний того, кто ее получил. Чем больше изменились знания получателя сообщения, тем большее количество информации содержит сообщение.
Другой вопрос - как измерить степень изменения знаний получателя. Например, в университете преподаватель может легко узнать степень изменения знаний студента - на экзамене. Однако он не может выяснить -почему один студент получил больше информации, а другой меньше. Поэтому важно объяснить сам процесс изменения знаний при получении сообщения. Одной из попыток описания этого процесса является модель Шрейдера.
В основе модели Шрейдера лежит понятие тезауруса.
Тезаурус (греч. - сокровище) - это знания человека, представленные в виде понятий и отношений между ними, т.е. определенным образом структурированное знание. Например, образ дерева, растущего на земле, можно представить в виде понятий: «дерево», «земля» и смыслового отношения между ними «расти на». Таким же образом можно представить и любой другой фрагмент нашего знания.
Утверждается, что человек извлечет информацию из сообщения, только в том случае, если изменится его тезаурус. Причем, чем сильнее изменения, тем больше информации.
Рассмотрим - как модель Шрейдера объясняет процесс передачи информации. Пусть источник сообщения - преподаватель, а получатель -студент. И у преподавателя и у студента есть свой тезаурус. Преподаватель на лекции сообщает студенту какие-то знания, т.е. фрагмент своего тезауруса. Возможны три ситуации.
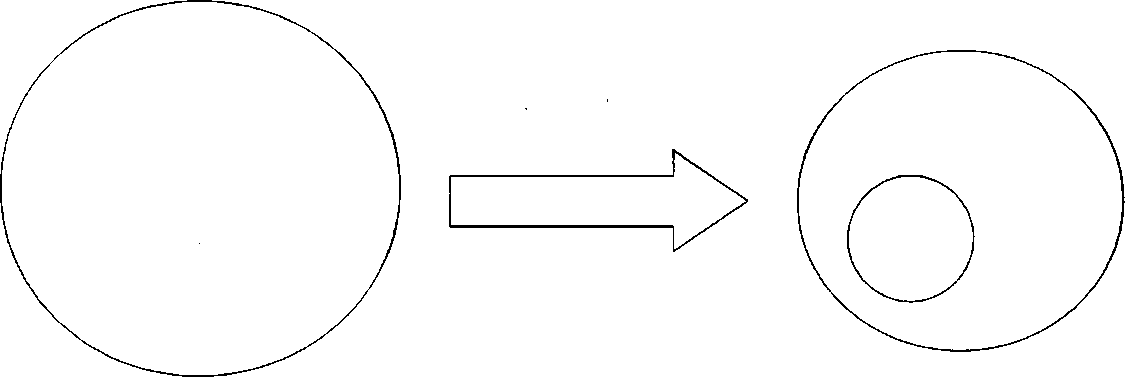
1) Сообщение полностью известно студенту (дважды два - четыре). Графически это можно представить как полное вхождение фрагмента тезауруса преподавателя (маленький круг) в тезаурус студента (рис.). Это ситуация «известно все». Тезаурус студента не изменяется и передачи информации не происходит.
2) Сообщение совершенно не понятно студенту (незнакомая математическая формула). Это значит, что фрагмент содержит понятия и отношения между ними, которых нет в тезаурусе студента (рис.). Это ситуация «неизвестно ничего». Как и в первом случае передачи информации не происходит.
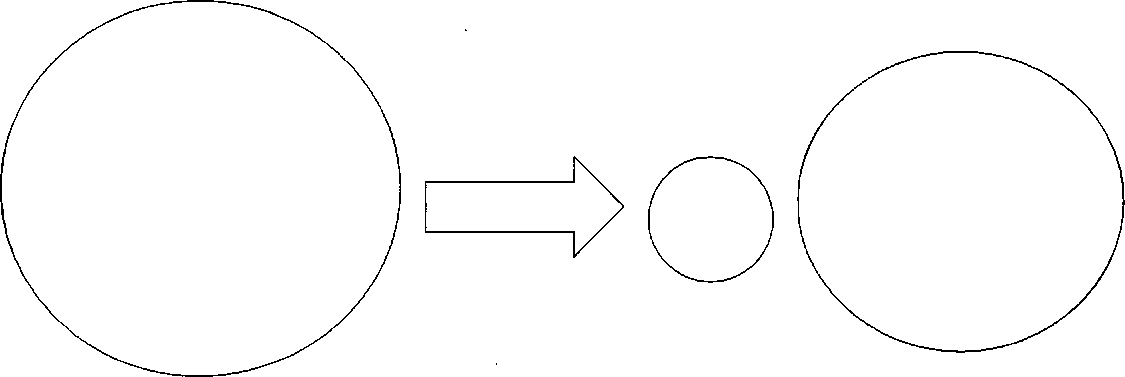
Тезаурус преподавателя Тезаурус студента
3) Фрагмент тезауруса преподавателя содержит часть понятий и отношений, которые есть в тезаурусе студента (заштрихованная область). Эта общая область играет важную роль в коммуникациях (процессах передачи знаний - обучении).
Тезаурус студента изменится и он получит информацию только в том случае, если неизвестные ему понятия и отношения можно выразить через уже имеющиеся (заштрихованная область). Если это не удается, то ввести новое понятие в тезаурус и изменить его невозможно. Таким образом, «непонятное» необходимо объяснять через «понятное».
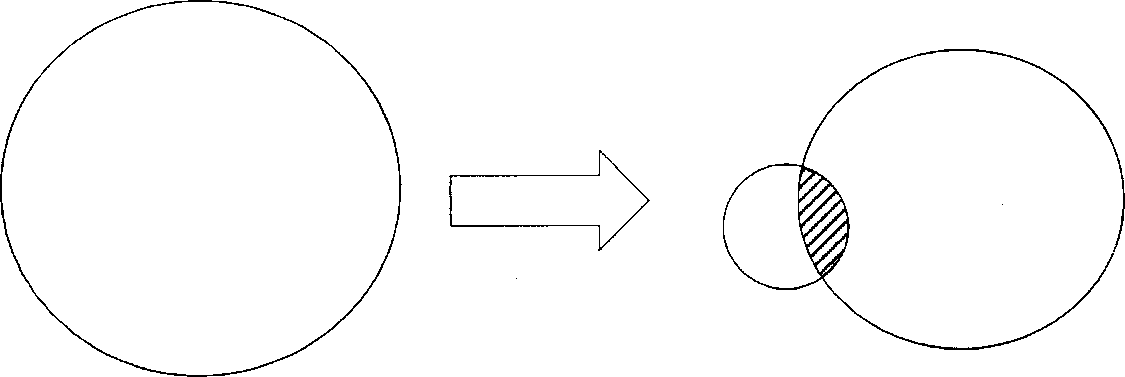
Например, преподаватель микроэкономики сообщает студенту, что закон спроса характеризует обратную зависимость между ценой продукции (р) и количеством (Q), которое захочет купить потребитель по этой цене. Если студент понимает, что такое цена и количество продукции, а также что такое обратная зависимость, то он сможет понять закон спроса - и его тезаурус увеличится.
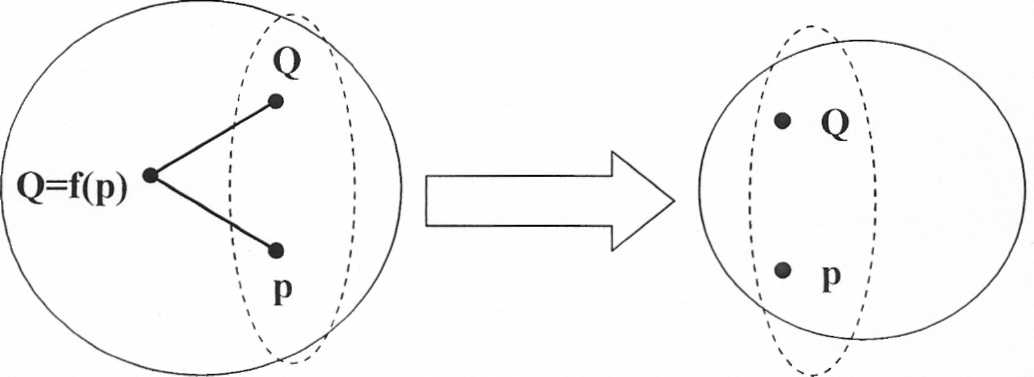
Фрагмент тезауруса преподавателя Тезаурус студента
Зависимость кол-ва полученной из сообщения информации от величины тезауруса можно представить. следующим образом. (рис)
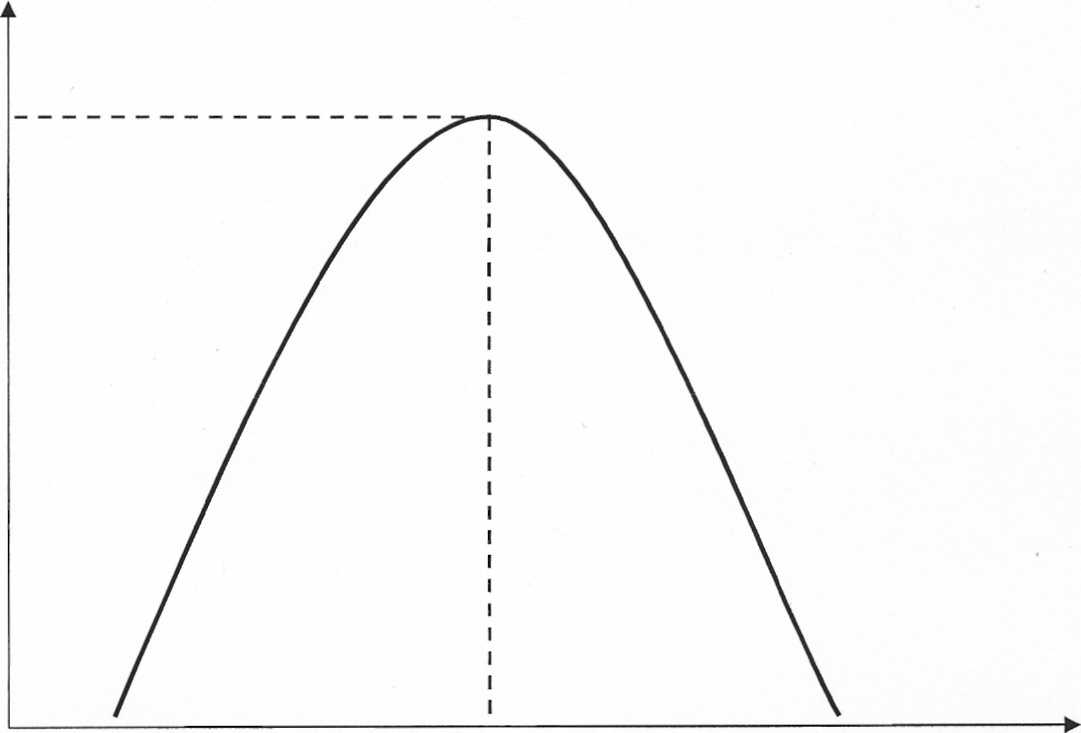
| min opt max Тезаурус получателя |
При минимальном тезаурусе (точка min) нельзя будет извлечь из сообщения информацию - „неизвестно ничего". При максимальном размере тезауруса (точка max) также не будет получена информация -„известно все". И, наконец, существует такой размер тезауруса, при котором будет получено максимум информации (точка opt).
Таким образом, эффективность коммуникации зависит от соотношения между тезаурусами отправителя и получателя сообщения. Отсюда, например, следует, что уровень изложения лекций для студентов разных курсов должен быть разным, так как тезаурус студентов постоянно расширяется.
Семантический подход подчеркивает, что информация для получателя всегда имеет относительную ценность, зависящую от его тезауруса.
