Классификация объектов при наличии обучающих выборок. Постановка задачи классического дискриминантного анализа
Дискра может проводиться несколькими методами:
а) в зависимости от реализованного алгоритма различают две группы методов дискра:
а.1. методы интерпретации межгрупповых различий по дискриминантным переменным, позволяющие установить отличия одного класса от другого;
а.2. методы классификации на основе дискриминантных функций, с помощью которых по выбранным признакам новые объекты распределяются по существующим классам.
б) по количеству обучающих выборок различают два вида методов дискра:
б.1. для двух групп - строится только одна дискриминантная функция;
б.2. для трех и более групп применяется множественный дискра - строится несколько дискриминантных функций.
в) в зависимости от правил дискриминации в литературе рассматривается три вида дискра:
в.1. линейный дискра Фишера – правила дискриминации представлены в виде линейной комбинации дискриминантных переменных;
в.2. канонический дискра – правила дискриминации представлены в виде дискриминантных функций;
в.3. линейный дискра - правила дискриминации представлены совокупностью характеристик групповая ковариационная матрица, групповой вектор средних, определитель ковариационной матрицы).
Пусть имеется множество М, состоящее из n объектов наблюдения, каждый i-ый объект которого описывается совокупностью р значений дискриминантный переменных признаков 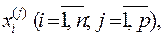 т.е. каждый объект представляет собой точку в р-мерном пространстве
т.е. каждый объект представляет собой точку в р-мерном пространстве 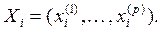 Причем все множество М объектов включает К (К
Причем все множество М объектов включает К (К  2) обучающих подмножеств
2) обучающих подмножеств  размером
размером 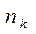 каждое и подмножество
каждое и подмножество 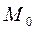 объектов, подлежащих дискриминации того же состава р дискриминантных переменных и, характеризуемых вектором
объектов, подлежащих дискриминации того же состава р дискриминантных переменных и, характеризуемых вектором 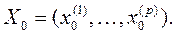 Здесь к – номер подмножества.
Здесь к – номер подмножества.
Наиболее часто используется линейная форма дискриминантной функции, которая представляется в виде скалярного произведения вектора дискриминантных множителей 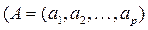 и вектора переменных
и вектора переменных 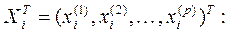
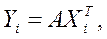 или
или 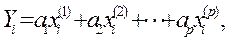 где
где 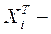 транспонированный вектор дискриминантных переменных
транспонированный вектор дискриминантных переменных 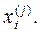
Основные предположения в теории дискра:
- множество М объектов разбито на несколько обучающих подмножеств, которые от других групп отличаются переменными 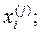
- в каждом подмножестве находится по крайней мере два объекта наблюдения
- 0<p<n-2. Число р обычно выбирается на основании логического анализа исходной информации
- между дискриминантными переменными существует линейная независимость (отсутствует мультиколлинеарность)
- все подмножества объектов гомоскедастичны, т.е. выполняется приблизительное равенство ковариационных матриц для каждого класса
- внутри каждого подмножества выолняется нормальный закон распределения
Если перечисленные условия не выполняются, то рассматривается вопрос о
целесообразности использования дискра для классификации остальных переменных. основные проблемы дискра – отбор дисриминантных переменных и выбор вида дискриминантной функции. Для получения наилучших различий обучающих подмножеств могут использоваться критерии последовательного отбора переменных или пошаговый дискра. После определения набора дискриминантных переменных решается вопрос о выборе вида дискриминантной функции (линейной или нелинейной). В качестве дискриминантных переменных могут выступать не только исходные (наблюдаемые) признаки, но и главные компоненты или главные факторы, выделенные в факторном анализе.
Дискра - совокупность статистических методов классификации многомерных наблюдений, используемых в ситуации, когда исследователь обладает так называемыми обучающими выборками.
Решается задача классификации n объектов, каждый из которых характеризуется значениями k показателей 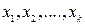 и p однородных в определённом смысле групп. Причём число p нам заранее известно. В основе ДА лежит матрица наблюдений размерности nxk:
и p однородных в определённом смысле групп. Причём число p нам заранее известно. В основе ДА лежит матрица наблюдений размерности nxk:
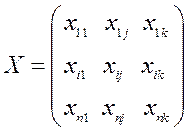 где
где 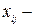 значение j-го показателя (j=1,2,…..k) для i-го наблюдения (i=1,2,…..,n). Тогда i-я строка матрицы содержит значения k признаков, характеризующих i-й объект. Имеется также p обучающих выборок:
значение j-го показателя (j=1,2,…..k) для i-го наблюдения (i=1,2,…..,n). Тогда i-я строка матрицы содержит значения k признаков, характеризующих i-й объект. Имеется также p обучающих выборок: 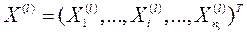 , где l=1,2,…,p. Таким образом l-я обучающая выборка представляет собой матрицу наблюдений размерности
, где l=1,2,…,p. Таким образом l-я обучающая выборка представляет собой матрицу наблюдений размерности 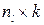 .При этом число p обучающих выборок равно общему числу всех возможных классов.
.При этом число p обучающих выборок равно общему числу всех возможных классов.
В ДА под однородной группой (классом) понимается ген. совокупность, описываемая одномодальным, наиболее часто k-мерным нормальным законом распределения с функцией плотности 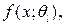 где
где 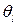 -вектор неизвестных параметров распределения, оценку которого
-вектор неизвестных параметров распределения, оценку которого 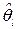 находят по обучающей выборке
находят по обучающей выборке 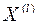 объёмом
объёмом 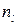 для l-го класса.
для l-го класса.
Получив оценку вектора параметров 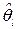 , находят оценку плотности распределения
, находят оценку плотности распределения 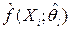 для i-го наблюдения, где i=1,2,…..,n и l=1,2,…..,p. Наблюдение
для i-го наблюдения, где i=1,2,…..,n и l=1,2,…..,p. Наблюдение 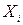 относят к той совокупности
относят к той совокупности 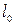 , которой соответствует наибольшее значение плотности
, которой соответствует наибольшее значение плотности 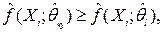 для всех l=1,2,…,p.
для всех l=1,2,…,p.
Процедуру классификации называют оптимальной, если среди всех других процедур она обладает наименьшими потерями от ошибочной классификации (отнесения объекта m-го класса к l-му).
