Простой случайный поиск
Статистические методы локального поиска
Статистические методы или методы случайного поиска получили достаточно широкое распространение при построении оптимальных решений в различных приложениях. Это объясняется в первую очередь тем, что с ростом размерности задач резко снижается эффективность регулярных методов поиска (детерминированных): так называемое “проклятие размерности”. Во-вторых, зачастую информация об оптимизируемом объекте слишком мала для того, чтобы можно было применить детерминированные методы. Достаточно часто статистические алгоритмы используют при поиске оптимального решения в системах управления, когда отклик системы можно получить только при задании управляющих воздействий 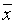 на ее входах. В таких ситуациях статистические алгоритмы могут оказаться значительно эффективнее детерминированных.
на ее входах. В таких ситуациях статистические алгоритмы могут оказаться значительно эффективнее детерминированных.

Рис.
Наибольший эффект применение статистических методов приносит при решении задач большой размерности или при поиске глобального экстремума.
Под случайными или статистическими методами поиска будем понимать методы, использующие элемент случайности либо при сборе информации о целевой функции при пробных шагах, либо для улучшения значений функции при рабочем шаге. Случайным образом может выбираться направление спуска, длина шага, величина штрафа при нарушении ограничения и т.д.
Статистические алгоритмы обладают рядом достоинств:
· простота реализации и отладки программ;
· надежность и помехоустойчивость;
· универсальность;
· возможность введения операций обучения в алгоритм поиска;
· возможность введения операций прогнозирования оптимальной точки (оптимального решения).
А основными недостатками являются большое количество вычислений минимизируемой функции и медленная сходимость в районе экстремума.
Принято считать, что преимущество статистических методов проявляется с ростом размерности задач, так как вычислительные затраты в детерминированных методах поиска с ростом размерности растут быстрее, чем в статистических алгоритмах.
Простой случайный поиск
Пусть нам необходимо решить задачу минимизации функции 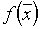 при условии, что
при условии, что 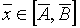 .
.
В данной области по равномерному закону выбираем случайную точку 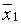 и вычисляем в ней значение функции
и вычисляем в ней значение функции 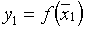 . Затем выбираем таким же образом случайную точку
. Затем выбираем таким же образом случайную точку 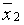 и вычисляем
и вычисляем 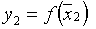 . Запоминаем минимальное из этих значений и точку, в которой значение функции минимально. Далее генерируем новую точку. Делаем
. Запоминаем минимальное из этих значений и точку, в которой значение функции минимально. Далее генерируем новую точку. Делаем 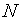 экспериментов, после чего лучшую точку берем в качестве решения задачи (в которой функция имеет минимальное значение среди всех случайно сгенерированных).
экспериментов, после чего лучшую точку берем в качестве решения задачи (в которой функция имеет минимальное значение среди всех случайно сгенерированных).
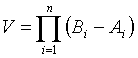 .
. 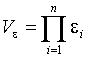 Вероятность попадания в эту окрестность при одном испытании равна
Вероятность попадания в эту окрестность при одном испытании равна 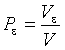 . Вероятность непопадания равна
. Вероятность непопадания равна 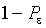 . Испытания независимы, поэтому вероятность непопадания за
. Испытания независимы, поэтому вероятность непопадания за 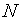 экспериментов равна
экспериментов равна 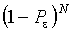 .
.
Вероятность того, что мы найдем решение за 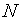 испытаний:
испытаний: 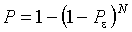 .
.
Отсюда нетрудно получить оценку необходимого числа испытаний 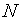 для определения минимума с требуемой точностью:
для определения минимума с требуемой точностью:
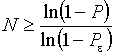 .
.
При решении экстремальных задач на областях со сложной геометрией обычно вписывают эту область в 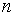 -мерный параллелепипед. А далее генерируют в этом
-мерный параллелепипед. А далее генерируют в этом 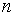 -мерном параллелепипеде случайные точки по равномерному закону, оставляя только те, которые попадают в допустимую область.
-мерном параллелепипеде случайные точки по равномерному закону, оставляя только те, которые попадают в допустимую область.
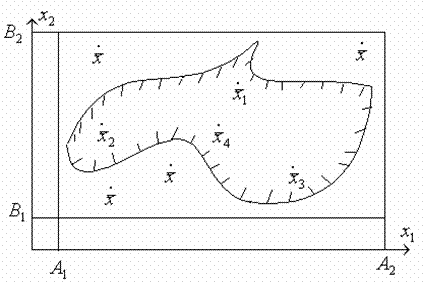
Рис.
Различают направленный и ненаправленный случайный поиск.
1. Ненаправленный случайный поиск. При таком поиске все последующие испытания проводят совершенно независимо от результатов предыдущих. Сходимость такого поиска очень мала, но имеется важное преимущество, связанное с возможностью решения многоэкстремальных задач (искать глобальный экстремум). Примером является рассмотренный простой случайный поиск.
2. Направленный случайный поиск. В этом случае отдельные испытания связаны между собой. Результаты проведенных испытаний используются для формирования последующих. Сходимость таких методов, как правило, выше, но сами методы обычно приводят только к локальным экстремумам.
