Лекция 2. Вероятностно-статистические методы распознавания
Вопрос 1. Метод Байеса
Основное преимущество статистических методов распознавания состоит в возможности одновременного учета признаков различной физической природы, так как они характеризуются безразмерными величинами – вероятностями их появления при различных состояниях системы.
Среди методов технической диагностики метод, основанный на обобщенной формуле Байеса, занимает особое место благодаря простоте и эффективности.
Разумеется, метод Байеса имеет недостатки: большой объем предварительной информации, «угнетение» редко встречающихся диагнозов и др. Однако в случаях, когда объем статистических данных позволяет применить метод Байеса, его целесообразно использовать как один из наиболее надежных и эффективных методов.
Метод, основанный на обобщенной формуле Байеса, позволяет достаточно просто одновременно учесть признаки различной физической природы – дискретные и непрерывные. Это достигается благодаря использованию единообразных и безразмерных характеристик признаков – частот встречаемости (вероятностей) признаков при различных состояниях.
Если имеется диагноз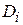 
и простой признак 
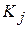, то вероятность совместного появления событий (наличие у объекта состояния 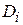и признака )
.
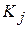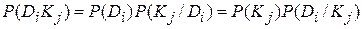Из последнего соотношения получаем
,
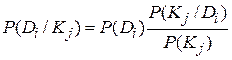где в последнем равенстве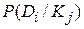 
– вероятность диагноза после того, как стало известно наличие у рассматриваемого объекта признака 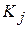(апостериорная вероятность диагноза); 
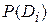– вероятность диагноза 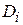, определяемая по статистическим данным (априорная вероятность диагноза). Если обследовано 
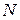объектов и состояние 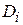наблюдается в 
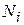изделиях, то
,
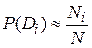где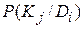 
– вероятность появления 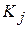объектов с состоянием 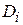. Если среди 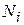объектов с диагнозом 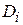у 
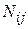появился признак 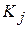, то
,
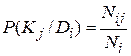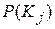– вероятность появления признака 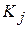во всех объектах независимо от его состояния (диагноза). Пусть из общего числа 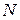признак 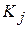обнаружен у 
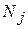объектов (с различным диагнозом). Тогда
.
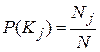Как будет ясно из дальнейшего, специальное вычисление 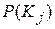не требуется.
Пусть проводится обследование ряда признаков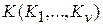 
по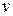 
многоразрядным признакам и 
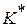означает определенную реализацию комплекса признаков. При этом в каждом из признаков 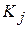проявляется один из разрядов, например в признаке 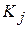разряд 
:
.
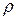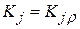Обобщенная формула Байеса (для комплекса многоразрядных признаков) имеет вид
.
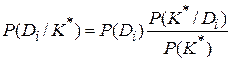
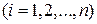В последнем равенстве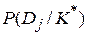 
– вероятность диагноза 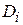, если комплекс признаков 
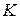получил реализацию .
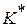Для независимых и зависимых признаков формула Байеса будет несколько отличаться. В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков при наличии существенных корреляционных связей.
Предъявленный для распознавания объект, обладающий комплексом признаков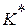 
, считают принадлежащем диагнозу 
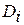, если
,
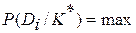т. е. вероятность диагноза 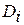оказалась наибольшей.
Сумма вероятностей всех диагнозов
.
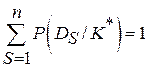Однако если вероятность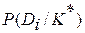 
не слишком велика (например, меньше 0,4 – 0,5), то следует отказаться от постановки диагноза. Поэтому решающее правило можно сформулировать следующим образом:
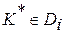если ,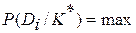
,
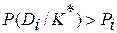где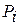 
– пороговое значение для диагноза 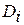(обычно принимают 
).
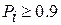Вопрос 2. Методы минимального риска
Методы минимального риска были развиты в связи с задачами радиолокации, но могут вполне успешно использоваться в задачах технической диагностики.
Пусть проводится измерение параметра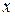 
(например, уровня вибраций изделия) и на основании данных измерений требуется сделать вывод о возможности продолжения эксплуатации (диагноз 
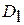– исправное состояние) или о направлении изделия в ремонт (диагноз 
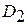– неисправное состояние).
На рис. 4 даны значения плотности вероятности диагностического параметра 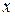для двух состояний.
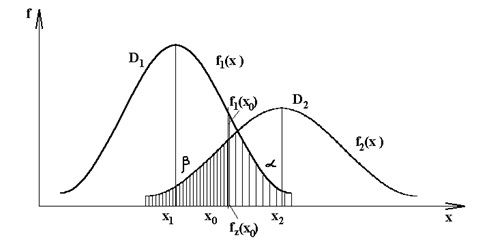
Рис. 4. Плотность вероятности диагностического признака
Пусть установлена контрольная норма для уровня вибрации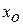 
. В соответствии с этой нормой принимают:
.
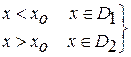Из рис. 4 следует, что любой выбор величины 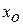связан с определенным риском, так как кривые 
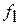и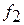 
пересекаются. Существуют два вида риска: риск «ложной тревоги», когда исправное изделие признают неисправным, и риск «пропуска цели», когда неисправное изделие считают годным.
В теории статистического контроля их называют риском поставщика и риском приемщика или ошибками первого и второго рода.
При 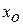вероятность ложной тревоги
,
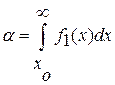вероятность пропуска цели
.
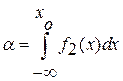Задача теории статистических решений состоит в выборе оптимального значения .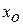
По способу минимального риска рассматривается общая стоимость риска
,
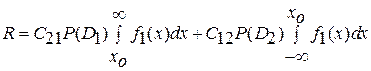где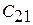 
– «цена» ложной тревоги; 
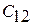– «цена» пропуска цел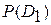и; 
и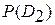 
– априорные вероятности диагнозов (состояний), определяемые по предварительным статистическим данным. Величина R представляет собой «среднее значение» потери при ошибочном решении.
Из необходимого условия минимума
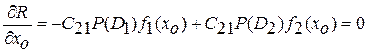
получаем
.
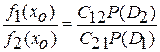Можно показать, что для одномодальных распределений данное условие всегда обеспечивает минимум величины R. Если стоимость ошибочных решений одинакова, то
.
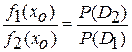Последнее соотношение минимизирует общее число ошибочных решений. Оно вытекает также из метода Байеса.
ЛИТЕРАТУРА
1. И.А.Биргер. Техническая диагностика. – М.: Машиностроение, 1978.
2. В.А. Пивоваров. Повреждаемость и диагностирование авиационных конструкций. – М.: Транспорт, 1994.
******************************************************************