Построение кодера и декодера ЦК. Формирование кодовой комбинации ЦК

Задача №1

Нарисовать кодер циклического кода, для которого производящий полином задан числом (4N+1); N=17, тогда 34+1=35₍₁₀₎=100011₍₂₎

P(x)=100011=1*x⁵+0*x⁴+0*x³+0*x²+1*x¹+1*x⁰=x⁵+x+1

Рис.12. Кодер циклического кода для производящего полинома

P(x)=x⁵+x+1

Задача №2. Записать кодовую комбинацию циклического кода для случая, когда производящий полином имеет вид Р(х)=x³+x²+1. Кодовая комбинация, поступающая от источника сообщений имеет К=4 элементов и записывается в двоичном виде как число, соответствующее N-8.

Для N=17-8=9₍₁₀₎=>1001₍₂₎, получим исходный многочлен А(х)=1000₍₂₎=x³+1

Решение будем производить по алгоритму:

1. Умножим полином A(x) на x^r, где r – число проверочных элементов: A(x)×x³=(x³+1)×x³=x⁶+x³.

2. Разделим полученный полином на производящий P(x):

1001000 1101

1101 1111

R(x)=011.

Окончательно имеем кодовую комбинацию на выходе кодера:

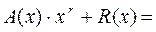1001011

Задача №3. Нарисовать кодирующее и кодовую комбинацию с целью декодирующее устройство с обнаружением ошибок и «прогнать» через кодирующее устройство исходную формирования проверочных элементов.

Производящий полином: Р(х)=x³+x²+1

При таком способе построения остаток от деления на Р(х) (проверочные элементы) сформируется на К такте. На вход подается информационная последовательность элементов. Если ключ находится в положении 1, то происходит деление на образующий полином и формируются проверочные элементы за К тактов. Информационная последовательность сразу же поступает на вход. Если ключ в положении 2, то сформированные проверочные элементы идут на выход кодера.

Прогоним кодовую комбинацию через кодирующее устройство:

Вх	№такт
			0
			1
0

Путем прогона исходной кодовой комбинации за К шагов получили проверочные элементы, где К - информационный элемент. Результаты полученные с помощью анализа и путем прогона через устройство совпали. Кодирующее устройство в котором будет производиться деление

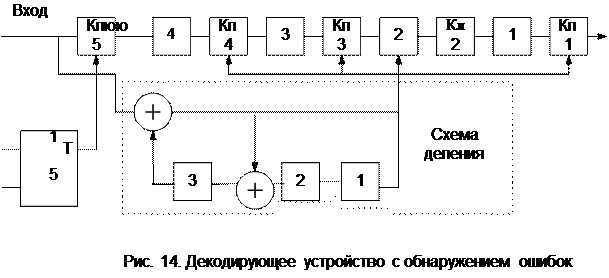на полином получит остаток, который будет записываться в три регистра.

Деление на производящий полином осуществляется за 7 тактов. Вначале КК стоят информационные элементы (четыре). В эти ячейки 1, 2, 3, 4 записываются информационные элементы, чтобы потом выдать их получателю.

После принятия всех 4 информационных элементов закрывается ключ Кл5 (в течении четырех тактов ключ 5 был открыт). На протяжении всего цикла записи информационных элементов Кл1, Кл2, Кл3, Кл4 были открыты. Если в результате деления на Р(х) получится остаток, то при этом Кл1, Кл2, Кл3, Кл4 запираются. В дальнейшем при сдвиге информации на один шаг вправо содержимое ячеек 1, 2, 3, 4 стирается (т.к. ключи были заперты).

Задача №4. Вычислить вероятность неправильного приема кодовой комбинации (режим исправления ошибок) в предположении, что ошибки независимы, а вероятность неправильного приема на элемент соответствует вычисленной в главе 2 (с учетом погрешности синхронизации и без учета погрешности синхронизации).

Вероятность неправильного приема вычисляется по формуле:

,

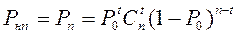где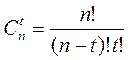

1. P_ош^(с)(e =0) = 0.016

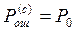- вероятность неправильного приема 1 элемента

P_n(2) = C₇^2.P₀^2.(1 – P₀)⁵ = 21^. 0.016^2.(1-0.016)⁵ = 0.005

T
Pn(t)	0.005	0.00013	2.19.10-6	2.13.10-8	1.11.10-10	2.68.10-13

Вероятность неправильного приема КК, для кода (7;4) d₀ и :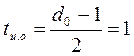

SP_n(t) =5,13^.10^-3

2.P_ош^(с)(e =22%) = 0,1159

Р₀=0.1159

T
Pn(t)	0,152	0,0333	0,0044	0,00034	1,5.10-5	2,8.10-7

SP_n(t) =0,19

Вероятность неправильного приема с учетом погрешности синхронизации больше, чем без учета погрешности синхронизации.

Системы ПДС с ОС.