Аффинные преобразования на плоскости
Вывод изображения на экран монитора и разнообразные действия с ним, в том числе и визуальный анализ, требуют от пользователя известной геометрической грамотности. Геометрические понятия формулы и факты, относящиеся к плоскому и трехмерному случаям, играют в задачах компьютерной графики особую роль. Геометрические соображения, подходы и идеи в соединении с постоянно расширяющимися возможностями вычислительной техники являются неиссякаемым источником существенных продвижений на пути компьютерной графики, ее эффективного использования в научных и иных исследованиях. Порой даже самые простые геометрические методики обеспечивают заметное продвижение на различных этапах решения большой графической задачи.
Аффинные преобразования - масштабирование, перенос, отражение или поворот геометрического объекта на плоскости или в пространстве.
В задачах компьютерной графики приходится иметь дело с несколькими различными системами координат на различных этапах решения. Все эти системы являются прямоугольными, то есть все оси перпендикулярны друг другу. Различия заключаются в направлении этих осей. Наиболее часто приходится учитывать разницу в направлении оси аппликат. Если ось аппликат направлена от нас (от зрителя, вглубь монитора и т. д.) система координат называется левосторонней, если наоборот, то правосторонней.
В компьютерной графике все, что относится к двумерному случаю, принято обозначать символом 2D[5].
Допустим, на плоскости введена прямолинейная координатная система. Тогда каждой точке М ставится в соответствие упорядоченная пара чисел (х ,у) ее координат. Вводя на плоскости еще одну прямолинейную систему координат, мы ставим в соответствие той же точке М другую пару чисел - (х* , у* ).
 | |||||
| |||||
|
Переход от одной прямолинейной координатной системы к другой описывается следующими соотношениями:
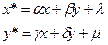 |
где α, β, δ, γ, λ, μ – произвольные числа, связанные неравенством
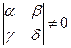 |
В дальнейшем мы будем рассматривать приведенные формулы как правило, согласно которому в заданной системе прямолинейных координат преобразуются точки плоскости.
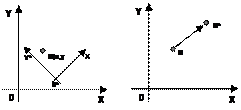
Эти формулы можно трактовать двояко: либо сохраняются координаты точки М и меняется координатная система, либо координатная система сохраняется и меняется положение точки (рис.61).
Рис.61
В аффинных преобразованиях на плоскости особую роль играют несколько важных частных случаев, имеющих хорошо прослеживаемые геометрические характеристики.При исследовании геометрического смысла числовых коэффициентов в приведенных формулах для этих случаев нам удобно считать, что заданная система координат является прямоугольной декартовой.
Поворот (вокруг начальной точки на угол φ )
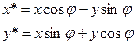
 |
Рис.62
