Сочетание методов многоуровневой передачи с фазовой манипуляцией

Несмотря на более высокую скорость передачи информации, достигаемую благодаря повы­шенной информационной емкости символа, многоуровневая передача в чистом виде не при­меняется. Выше уже было отмечено, что помехи и шумы в канале, а также ограничения на уровень сигнала в усилителях воздействуют, прежде всего, на амплитуду. Поэтому рас­сматриваемый способ не нашел применения. Однако, в сочетании с другими способами (в частности, с частотными манипуляциями) он дает высокий эффект и хорошую помехо­устойчивость. Наибольшее распространение получило сочетание многоуровневой передачи с фазовой модуляцией. (Модуляция — это процесс изменения параметров несущей частоты (амплитуды, частоты, фазы); манипуляция — это процесс воздействия на параметры несу­щей частоты цифровым сигналом.) Это позволило резко расширить полосу пропускания на абонентском участке. Ниже рассмотрен один из таких способов — фазовая манипуляция.

Фазовая манипуляция

Фазовая манипуляция преобразует информацию путем воздействия на фазу частотного сигнала. Например, в простейшем случае передачи отдельных бит (рис. 29) при переходе от 0 к 1 фаза меняется на 180°. В ситуации, показанной на рис. 29, а, единице соответству­ет положительный период в начале цикла, а нулю — отрицательный.

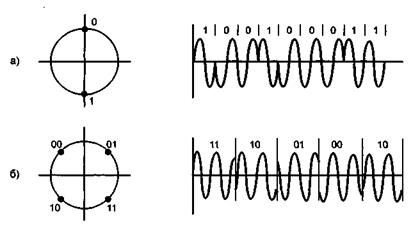
Рис. 29. Примеры фазовой манипуляции для случаев: а) 2-ФМ б) 4-ФМ

При способе фазовой манипуляции 4-ФМ (рис. 29, 6) сдвиг по фазе составляет 45°, при этом он кодируется следующим образом:

для 11 — сдвиг +45° (π/4);

для 10 — сдвиг +135° (З π /4);

при 00 — сдвиг +225° (-З π /4);

при 01 — сдвиг 315° (-π /4).

Фаза определяется с помощью измерения значения косинусоидального сигнала в начале периода.

Слева на рисунках показаны круговые диаграммы синусоидального сигнала (на рис. 29, б сигнал показывает значения косинуса, и потому сдвинут на 90°). Изменение значения синусои­дального сигнала сопоставляется со значением, изображаемым на круге. При этом с изменени­ем времени воображаемый вектор (радиус, помещенный в центр круга) вращается против часо­вой стрелки. Точка на круге показывает значение синусоидального сигнала в данный момент времени. Нижняя точка на круге соответствует минимальному отрицательному значению ам­плитуды и сопоставляется с дискретной единицей, а высшая точка соответствует максимально­му значению и отождествляется с дискретным нулем. Для диаграммы, показывающей четырех­кратный сдвиг фазы, намечены 4 точки.

В отличие от амплитудной модуляции, фазовая манипуляция менее подвержена воздей­ствию на уровень передачи (влиянию на амплитуду) и частоту. Она наиболее приспособле­на к передаче многоуровневых сигналов, которые, как следует из предыдущего раздела, по­зволяют повысить скорость передачи информации, не повышая линейную скорость в кана­ле. Однако на нее сильно влияют индуктивные и емкостные параметры кабеля. Например, уже упомянутые пупиновские катушки, улучшая параметры обычного сигнала, вносят искусственную индуктивность, которая, в свою очередь, влияет на сигналы, уплотненные с помощью фазовой манипуляции.

Форма модулированного сигнала при фазовой манипуляции определяется формулой:

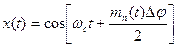
где 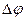= 2π/п — величина, на которую отличаются фазы соседних сигналов; тn — симмет­ричный n-уровневый сигнал в виде импульсов постоянного тока без возвращения к нулю, а значения уровней равны ±1, ±3 и т.д.

Последнее выражение легко приводится к виду:

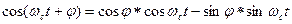
Формула позволяет свести процесс фазовой манипуляции к комбинации амплитудной модуляции двух последовательностей сигналов.

Представление синусоидального колебания как линейной комбинации синусоидального и косинусоидального колебаний с нулевой начальной фазой называется квадратурным пред­ставлением.

Функции совф иэтф для каждого такта передачи сигнала являются постоянными, т.е. играют роль коэффициентов, принимающих значения в соответствии с уровнем сигнала. Функци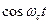и и 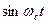играют роль несущих частот, сдвинутых на 90°. При сложении двух амплитудно-модулированных сигналов получается одна функция с фазовой модуляци­ей. Косинусоидальные сигналы обычно называют сигналами «в фазе» или «В-сигналами», а синусоидальные — сигналами «в квадратуре» или «К-сигналами».

Структурная схема фазового модулятора (ФМ), построенного по этому принципу, по­казана на рис. 30.

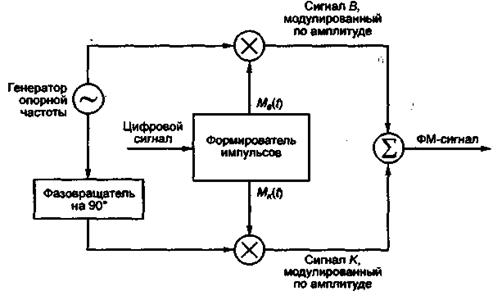
Рис. 30 Обобщенная схема фазового модулятора: MB(t) — В-сигнал; Mk(t) — К-сигнал