Логические формулы понятий
Любое понятие можно выразить в виде логической формулы, в которой элементы, образующие понятия, представлены предикатами и соединены логическими операциями конъюнкции, дизъюнкции и отрицания. В зависимости от вида этой формулы представляемые ею понятия можно классифицировать на простые и сложные.
Простое понятие Р (Х) представляется логическим выражением
n
P(X)ß& Ai (z 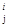 , X), (3)
, X), (3)
i=1
Где z 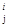 Î dom Ai —j –e значение признака Ai, a Ai (z
Î dom Ai —j –e значение признака Ai, a Ai (z 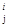 , X)—предикат истинный, если признак Ai сущности X принимает значение z
, X)—предикат истинный, если признак Ai сущности X принимает значение z 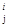 , иначе - ложный.
, иначе - ложный.
Для данного понятия в логической формуле может присутствовать не более одного значения некоторого признака Ai. Это логическое выражение допускает простую интерпретацию любая сущность X, обладающая совокупностью признаков z 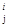 Î dom Ai является денотатом данного понятия Р (Х).
Î dom Ai является денотатом данного понятия Р (Х).
Если допускается несколько значений данного признака Ai, то для такого понятия справедлива логическая формула
n
Р (Х) & Ai (z 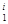 , X)
, X) 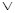 Ai (z
Ai (z 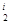 , X)
, X) 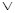 ...
... 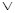 Ai (z
Ai (z 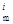 , X). (4)
, X). (4)
i=1
Признаки, которые могут принимать несколько значений, называются множественными.
Более сложный класс понятий описывается дизъюнктивно-конъюнктивными логическими выражениями вида
P (X) Q1 (X) 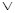 Q2 (X)...
Q2 (X)... 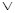 Qm (X), (5)
Qm (X), (5)
n
где Qk (X) = & P 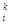 (X) и P
(X) и P 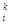 (X)—предикаты, входящие в k-й дизъюнкт.
(X)—предикаты, входящие в k-й дизъюнкт.
i=1
Выражение вида (5) фактически определяет понятие Р (X) через m альтернативных понятий Qk (X), каждое из которых является конъюнкцией предикатов P 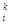 (X).
(X).
В связи с этим без потери общности можно считать, что любое понятие может быть представлено формулой
n
Р (Х) & Pi (X), (6)
i=1
где Pi (X)—предикаты, которые могут интерпретироваться как другие понятия или как признаки понятия Р (Х).
Если учесть деление признаков понятия Р (Х) на дифференциальные, характеристические и валентные, то логическое выражение (6) можно представить в виде:
n m l
Р (Х) & Di (d 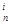 , X) & Нj (h
, X) & Нj (h 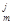 , X) & Vk (v
, X) & Vk (v 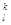 ,X), (7)
,X), (7)
i=1 j=1 k=1
где d 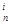 Î dom Di—значения дифференциальных признаков Di.
Î dom Di—значения дифференциальных признаков Di.
Устанавливая различные значения дифференциальных признаков, мы получаем класс понятий с однородной структурой: все понятия данного класса обладают одинаковой схемой.
Таким образом, наиболее удобным аппаратом формализации понятий, используемых для представления знаний о фактах, действиях, событиях, ситуациях и т. д., является логика исчисления предикатов. Ограничиваясь правилами, формулируемыми на основе хорновских дизъюнктов, мы получаем простой и достаточно общий способ выражения связей как между признаками и понятиями, так и между различными понятиями.
Концепт понятия
Каждое имя понятия, кроме того, что оно может замещать некоторую конкретную сущность, связывается с теми общими свойствами (признаками), которые присущи всем сущностям, составляющим множество всех денотатов данного понятия. Совокупность всех признаков, позволяющих идентифицировать данное понятие, называется концептом, или содержанием, понятия. Концепт понятия указывает необходимую информацию, с помощью которой данная сущность или предмет могут быть отнесены к некоторому множеству однотипных сущностей, т. е. концепт содержит знания о потенциальном денотате и характеризует определенный класс возможных денотатов [67]. Концепт коллегия включает в себя как все собственные признаки понятия, так и те признаки, которые позволяют установить связь данного понятия с другими понятиями (валентные признаки), т. е. концепт включает схему строения понятия. Если понятие является сложным, то его концепт содержит также информацию о концептах понятия, входящих в данное понятие.
Таким образом, в концепте понятия отражается вся информация, необходимая для принятия решения об отнесении некоторой сущности к денотату понятия. В более сложных случаях концепт включает совокупность правил, необходимых и достаточных для принятия решения о принадлежности данной сущности объему понятия. Это означает, что концепт является носителем семантики понятия. Другими словами, концепт—это то знание, которое выражается данным понятием при концептуальном моделировании предметной области [67].
