Расчет надежности невосстанавливаемых систем с постоянным резервом
Общее постоянное резервирование с целой кратностью. Вероятность отказа Qp параллельно работающих тэлементов при r = 1определяется выражением (3.2), откуда для равнонадежныхэлементов
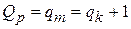 ;
; 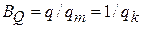 . (3.8)
. (3.8)
Чем меньше вероятность отказа каждого из элементов, тем выше эффективность постоянного резервирования. Так, если q = 0,1 и 0,01, а k = 1, то выигрыш в снижении вероятности отказа при резервировании составит соответственно 10 и 100. Рассмотрим связь показателей надежности группы резервированных элементов, кратности резервирования k и длительности работы элементов t при экспоненциальном законе распределения времени их безотказной работы. Если интенсивность отказов каждого из элементов 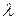 , то согласно (1.12), (1.21), (1.22) имеем
, то согласно (1.12), (1.21), (1.22) имеем
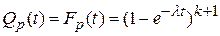 ;
; 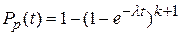 ; (3.9)
; (3.9)
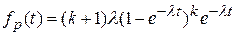 ;
;
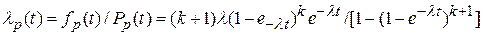 ;
;
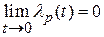 ;
; 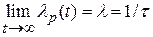 .
.
Графики изменения PP(t/ 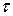 )и
)и 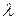 р(t/
р(t/ 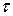 )/
)/ 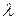 в зависимости от кратности резервирования и длительности работы системы представлены на рис. 3.7. Они показывают, что постоянное резервирование эффективно на начальном участке работы системы, когда t
в зависимости от кратности резервирования и длительности работы системы представлены на рис. 3.7. Они показывают, что постоянное резервирование эффективно на начальном участке работы системы, когда t 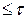 .
.
Для группы резервированных элементов средняя наработка до отказа
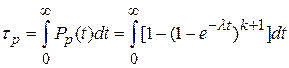 .
.
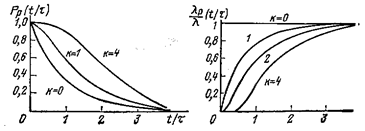
Рис. 3.7 Графики зависимости вероятности безотказной работы (а) и интенсивности отказов (б) от кратности резервирования
Работа рассматриваемой группы резервированных элементов характеризуется последовательным переходом по мере возникновения отказов от т работающих элементов к т–1, т–2 и далее до одного, отказ последнего приводит к отказу всей группы. Эту последовательность переходов иллюстрирует график, представленный на рис. 3.8. В случайные моменты времени t1, t2и т. д. происходят отказы элементов, число работающих элементов n(t)постепенно снижается. Поскольку на каждом из участков T1 = t1, T2 = t2 – t1и т. д. имеет место совместное функционирование т, т-1и т. д. элементов, то случайные интервалы времени T1, Т2,...,Тт имеют экспоненциальное распределение с интенсивностями отказов соответственно m 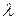 , (т–1)
, (т–1) 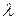 , ...,
, ..., 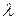 и средней продолжительностью
и средней продолжительностью 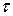 1 = 1/(m
1 = 1/(m 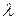 ),
), 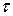 2 = 1/[(т–1)
2 = 1/[(т–1) 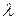 ],
], 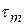 = 1/
= 1/ 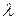 . Поскольку
. Поскольку 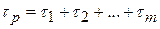 , то значение средней наработки до отказа группы резервированных элементов определяется как
, то значение средней наработки до отказа группы резервированных элементов определяется как 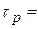 1/(m
1/(m 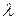 )+1/[(т–1)
)+1/[(т–1) 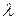 ]+ 1/
]+ 1/ 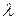 .
.
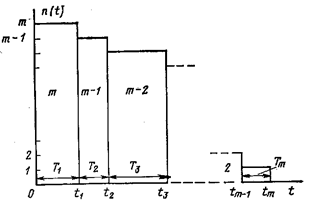
Рис. 3.8 Временная диаграмма изменения числа параллельно функционирующих устройств
Резервирование двухполюсных элементов. В большинстве случаев резервные элементы подключают параллельно основному. Однако при дифференциации видов отказов резервирование по каждому из них может осуществляться при различных способах включения резервных элементов. Наиболее характерным в этом отношении является резервирование элементов при отказах типа «обрыв» и «короткое замыкание» (КЗ). Для двухполюсных элементов релейного типа, имеющих два возможных состояния 1 и 0, этим отказам соответствует несрабатывание при наличии управляющего сигнала и ложное срабатывание при отсутствии последнего.
При последовательном соединении релейных элементов (рис. 3.9,а) несрабатывание любого из элементов приводит к отсутствию цепи между точками а и b. Таким образом, для этого вида отказов последовательное соединение релейных элементов является основным. Для отказов типа ложное срабатывание последовательное соединение является резервным, поскольку этот вид отказа цепи будет иметь место только при отказе двух элементов.
Из рассмотренного вытекает, что одному и тому же соединению элементов для этих видов отказов соответствуют две структурные схемы. При последовательном соединении релейных элементов осуществляется резервирование по отказам типа КЗ. Если вероятность отказов этого типа для каждого элемента q, то Ba = q/q2 = q-1.Для отказов типа обрыв 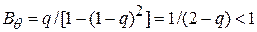 , т. е. последовательное включение релейных элементов приводит к повышению вероятности возникновения отказов типа обрыв цепи. При параллельном соединении релейных элементов (рис. 3.9,б) осуществляется резервирование по отказам типа обрыв с эффективностью BQ = 1/q, а по отказам типа КЗ надежность снижается.
, т. е. последовательное включение релейных элементов приводит к повышению вероятности возникновения отказов типа обрыв цепи. При параллельном соединении релейных элементов (рис. 3.9,б) осуществляется резервирование по отказам типа обрыв с эффективностью BQ = 1/q, а по отказам типа КЗ надежность снижается.
Резервирование с дробной кратностью. При резервировании с дробной кратностью система может функционировать, если из п однотипных работающих параллельно элементов в работоспособном состоянии находятся r. Система отказывает, если число отказавших элементов z составляет 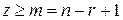 . Используя метод перебора состояний, определим вероятность отказа такой системы
. Используя метод перебора состояний, определим вероятность отказа такой системы
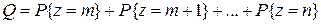 .
.
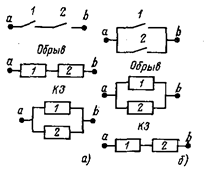
Рис. 3.9 Схемы последовательного (а) и параллельного (б) соединения релейных элементов и соответствующие им структурные схемы
В каждом из состояний число работоспособных элементов составляет п – z, а вероятность этого состояния 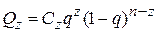 ,тогда
,тогда
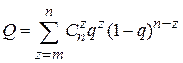 , (3.10)
, (3.10)
где Cnz = n!/[z!(n–z)!] – число сочетаний из п элементов по z, причем 0! = 1; 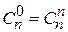 =1. При
=1. При 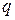 <<1
<<1 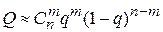 .
.
При экспоненциальном законе распределения времени безотказной работы и интенсивностях отказов 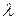 каждого из элементов
каждого из элементов
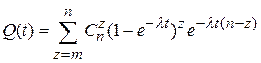 . (3. 11)
. (3. 11)
Поскольку без резерва система включает r работающих элементов, то вероятность отказа исходной системы при оценке эффективности резервирования составляет 1–(1–q)r. Так, если система включает три параллельно работающих элемента и r = 2, то при q = 0,1, k = 1/2, т = 2согласно (3.11)
Q = 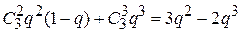 ;
;
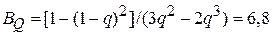 .
.
