Позиционные системы количественных показателей

Самые простые типы позиционного подсчета отражают показатели кандидата, ранжированные выше или ниже среднего, либо ранжированные в убывающем порядке от лучшего к худшему. Например кандидат А занимает третью позицию в тесте А, пятую в тесте В и девятую в тесте С. Однако поскольку ранжирование зависит от того, сколько человек выполняют тест, позиционирование кандидата меняется, когда тест выполняют меньшее или большее число человек; это осложняет проведение обоснованной оценки, насколько качественно по сравнению с другими выполняет тест кандидат. Другие трудности заключаются в том, что способности или достоинства кандидата не отражаются при позиционировании. Все кандидаты, выполняющие тест, могут обладать большими или меньшими достоинствами по сравнению с теми, кто составлял предыдущие группы.

Усовершенствованный тип позиционного подсчета — процентили. Они помещают кандидата в репрезентативную очередь по отношению к 99 другим (см. Таблицу А.1). Процентильное позиционирование показывает количественное соотношение: сколько других кандидатов получили более низкие показатели, чем кандидат, позиционированный на этом конкретном процентиле. Например позиционирование кандидата А на 75-м процентиле указывает, что 75 процентов выполнивших тест кандидатов получили худшие показатели, чем кандидат А. Это происходит потому, что система базируется на процентильных показателях от О до 100, где 0 — худший показатель, а 100 — лучший. В группе из 100 человек, каждый из которых получил отличный от другого показатель, кандидат с процентильным показателем 50 будет помещен в очередь пятидесятым, а кандидат с процентильным показателем 60 — шестидесятым. На самом деле из-за способа обычной дистрибуции человеческих характеристик процентильные шкалы могут вводить в заблуждение, если их значение понимают неправильно. Рассмотрим, например, как могут распределиться показатели теста на математические способности '100 человек. Совсем немногие кандидаты получат очень высокие или очень низкие показатели, а большинство будет находиться примерно посередине. Кандидаты в первой десятке могут получить показатели примерно от 80 до 95 (разница в 15 пунктов). В середине диапазона показателей, в силу того, что показатели будут находиться очень близко друг от друга, 50-й процентиль может распределиться примерно от 47 до 50 (разница в 3 пункта). Другими словами, разница в процентильных показателях не отражает разницы реальных показателей. С точки зрения разницы выполнения теста, разрыв между двумя кандидатами, позиционируемыми на 90-м и 95-м процентилях, скорее всего, будет гораздо больше, чем разрыв между двумя кандидатами, позиционируемыми на 50-м и 55-м процентилях. Тем не менее — даже учитывая это предостережение, — процентильные показатели предлагают два преимущества: возможность сравнить кандидата со всеми другими кандидатами, выполняющими конкретный тест; и возможность оценить показатели других тестов тех же кандидатов по отношению друг к другу. Основной недостаток заключается в том, что процентильные показатели не указывают, какова разница между показателями теста каждого кандидата, поскольку они только регистрируют сравнительные достижения кандидатов в рамках отдельного теста.

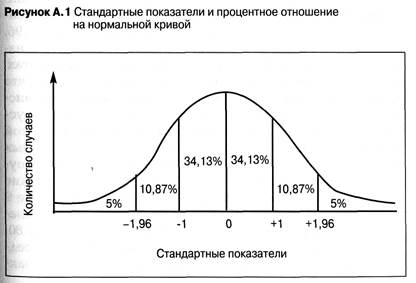
Если требуется более точная и обоснованная оценка сравнительных достижений, необходимо принимать в расчет не только ранжирование кандидатов, но и величину разницы между ними. Именно это обеспечивает система количественных показателей, базирующаяся на нормальной кривой, с помощью стандартных показателей. Свойства нормальной кривой (см. Рис. А.1) предполагают, что одно среднее отклонение (негативное или позитивное) будет уравнивать, где будут находиться 68,26 процентов всех показателей теста, два средних отклонения будут уравнивать, где будут находиться 95,44 процентов всех показателей, а три средних отклонения будут уравнивать, где будут находиться 99,74 процентов всех показателей теста (более подробное обсуждение этого вопроса см. в работе Миллера (Miller), 1984). Это свойство нормальной кривой обеспечивает простой способ соотношения процентилей и показателей кандидатов, с тем чтобы получить более обоснованную информацию при помощи стандартных показателей.

Стандартные показатели указывают, где находятся показатели кандидата по отношению к среднему количественному показателю всех кандидатов в отдельном тесте (то есть выше или ниже среднего количественного показателя), и показывают, насколько сильно стандартный показатель отличается от среднего количественного показателя. Эти два качества стандартных показателей просто отражают две основные характеристики нормальной кривой: среднее значение и среднее отклонение. Среднее значение демонстрирует средний показатель всех кандидатов, участвующих в тесте, в то время как среднее отклонение указывает, насколько показатель отличается от среднего количественного показателя, и как таковое является средством измерения разброса данных.

Таблица А. 1Процентильная система

Показатель	Процентиль
64-70
0-20

Простейшим видом стандартного показателя является показатель Z, просто устанавливающий, на сколько средних отклонений кандидат находится выше или ниже среднего. Кандидат с показателем Z, равным нолю, находился бы точно на среднем значении, кандидат с показателем Z, равным минус два (— 2) (то есть негативным показателем), находился бы на два средних отклонения ниже среднего значения, а кандидат с позитивным показателем Z, равным 1,56, находился бы на 1,56 средних отклонений выше среднего значения. Преобразование необработанных показателей теста в показатели Z делается очень просто. Нужно вычесть необработанные показатели теста из среднего количественного показателя теста и разделить на величину разброса (то есть среднего отклонения). Большинство публикуемых тестов обеспечивают среднее значение и среднее отклонение, базирующиеся на стандартной таблице. Например, если тест имеет среднее значение 75 и среднее отклонение 15, то кандидат, получивший показатель теста 90, имел бы показатель Z в размере 1: то есть (90 — 75)/15 = 1.

Преимущества использования показателей, базирующихся на нормальной кривой, для разграничения кандидатов заключаются в том, что кандидата можно позиционировать по отношению к другим и при этом также можно определить величину разницы между показателями теста. Кроме того, показатели, базирующиеся на нормальной кривой, избегают искажения или преувеличения различий между кандидатами, потому что величина разницы между средними отклонениями одна и та же. Таким образом, анализировать и интерпретировать показатели теста проще в известной степени.

Как было отмечено выше, связь между стандартными показателями и процентилями можно использовать с хорошими результатами. Стандартный показатель + 1 указывает на выполнение теста, которое лучше среднего значения на одно среднее отклонение. Как показывает Рис. АЛ, известно, что на нормальной кривой отдельное процентное соотношение кандидатов (84,13 процентов) получит стандартный показатель менее +1, и 15,87 процентов получат лучший показатель. Таким способом стандартные показатели могут переводиться в процентильные, и наоборот. Например, чтобы получить показатели в верхних пяти процентах, кандидату нужен стандартный показатель +1,96. Аналогичным образом стандартный показатель — 1,96 означал бы, что кандидат находится в нижних пяти процентах. Небольшой недостаток стандартных показателей — то, что они включают отрицательные и положительные знаки числа, а также десятичные запятые; и то и другое иногда упускают, когда выписывают результаты. Чтобы избежать этой проблемы, можно использовать другие виды стандартных показателей, преобразовав показатель Z. Во многих популярных психологических тестах часто применяются такие показатели, как: 16PF, показатели Т, показатели на базе 9 или показатели на базе 10. Показатель Т имеет среднее значение 50, среднее отклонение 10 и диапазон от 20 до 80. Показатели на базе 10 имеют среднее значение 5,5 и среднее отклонение 2. Недостаток показателей на базе 10 заключается в использовании половинных значений, а также двухзначных чисел при подсчете для тех, кто получил максимальные показатели. Показатели на базе 9 имеют среднее значение 5 и сходны с показателями на базе 10, за исключением того, что стандартные показатели лежат в диапазоне от 0 до 9. Каждый из этих преобразованных стандартных показателей избегает использования показателей ниже 0 и может быть рассчитан в процентилях напрямую.