Терминалы и принципы преобразования информации

Сказанное можно пояснить на простом примере. Для восстановления синусоидального сигнала необходимо иметь для каждого полупериода хотя бы две опорные точки. Тогда сглаживающий фильтр хотя бы приблизительно восстановит исходную форму. При этом может быть получено множество огибающих кривых в зависимости от характеристик этого фильтра. При большем числе точек форма огибающей восстанавливается точнее. При числе точек менее, чем две, огибающая не восстанавливается, более того, получается сигнал дру­гой частоты (рис. 22). При недостаточной частоте дискретизации может быть получен сигнал меньшей частоты, но совпадающий по значению во всех точках дискретизации.

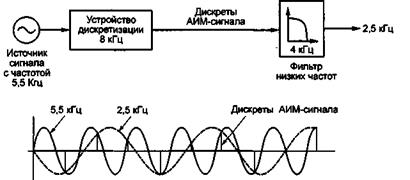
Рис. 22 Преобразование сигнала при недостаточной частоте дискретизации

В случае несинусоидального сигнала надо говорить о восстановлении всего спектра частот. При этом, если частота импульсной последовательности окажется выше максималь­ной частоты спектра, она не повлечет на приемном конце искажения более низких частот. Поэтому даже при выборе достаточной частоты импульсной последовательности дискрети­зации в реальных устройствах преобразования сигналов на входе передатчика ставят фильтр, который не пропускает сигналы с частотой выше принятой частоты пропускания. Это дела­ется по следующей причине: появление подобных частот приведет к тому, что если на вхо­де появятся сигналы, для которых период опроса мал, то после восстановления на прием­ном конце могут появиться сигналы в пределах допустимого спектра.

На рис. 22 показан процесс возникновения помех на примере, когда сигнал с частотой 5,5 кГц дискретизируется с частотой в 8 кГц.

При определенных соотношениях амплитуд значения дискрет, получаемые для более высокой частоты 5,5 кГц, совпадают со значениями, получаемыми для более низ­кой частоты. При прохождении выходного фильтра с частотой среза 4 кГц возникает сигнал с частотой 2,5 кГц, который не поступал на вход. Этот пример показывает, что из входного сигнала перед дискретизизацией должны быть отделены все сигналы, имеющие частоту вы­ше, чем fдискр/2. Необходимо заметить, что применение таких фильтров в тракте ухудшает условия для передачи высокоскоростных данных и при комбинированном (интегральном) использовании тракта. При необходимости эти фильтры должны отключаться.

Рассмотренный выше принцип позволяет перейти от непрерывного сигнала к дискрет­ному. При этом каждый дискретный отсчет несет информацию о значении сигнала (ампли­туде) в момент отсчета. Этот способ передачи получил название «амплитудно-импульсная модуляция» (АИМ). Однако такой способ обмена сигналами оказался непомехоустойчи­вым. Помехи в первую очередь действуют на амплитуду сигнала, искажения амплитуды.

Происходят при прохождении сигнала через усилители, поскольку каждый усилитель имеет ограничение по частоте. Поэтому этот способ применялся недолго и вскоре был заменен способом импульсно-кодовой модуляции, принцип которого заключается в том, что вместо сигнала с конкретной амплитудой передается его числовое значение.

Чтобы реализовать такой переход, необходим процесс квантования, который осуществ­ляется аналого-цифровым преобразователем — АЦП.

Квантование

Процесс квантования заключается в определении значения амплитуды каждого отсче­та и присвоении этой величине соответствующего двоичного значения. Самое простое — это равномерное квантование. При этом типе квантования диапазон амплитуды входного сигнала (при равномерном квантовании он обычно составляет 30 дБ) разбивается на под­диапазоны с одинаковой величиной шага. Внутри каждого шага величина измеряемого сигнала считается постоянной. Величина исходного сигнала может принимать любое зна­чение между шагами квантования. Однако на выходе сигналу присваивается значение в точке начала квантового шага и оно сохраняется неизменным до его конца. Это значение передается в виде кода, обозначающего номер кванта. На приемном конце этот номер де­кодируется равным значению в середине шага квантования. В табл. 1.1. показан пример квантования сигнала.

Таблица 1.1. Пример квантования

Момент времени	Исходный сигнал	Присвоенный код	Значение, восстановленное на приеме
Знак	Код	Десятичное значение кода
t1	-1,9				-1,5
t2	-1,7				-1,5
t3	-0,1				-0,5
t4	+2,8				+2,5
t5	+5,8				+5,5
t5	+5,3				+5,5

В первом столбце таблицы приведены моменты времени квантования.

Во втором приведены значения исходного сигнала в эти моменты времени.

В следующем столбце приведен код, присвоенный после квантования. Он состоит из:

знака сигнала (1 — обозначает отрицательный сигнал, 0 — положительный);

кода сигнала на передаче.

Код сигнала указывает номер кванта. Шаг квантования принят 1. Всего имеется 6 шагов квантования. При этом сигналы -1,9 и -1,7 имеют отрицательный знак (1), а код сигнала (номер кванта) -2 (010).

Два сигнала +5,8 и +5,3 имеют положительный знак (0) и закодированы номером кванта (ПО). На приемном конце их значение +5,5.

В реальной системе для передачи речи (построения станции) выбраны 256 квантов. Это число позволяет обеспечить хорошую разборчивость речи. Для двоичного кодирования та­кого числа квантов нужно 8 разрядов. Максимальная принятая частота речевого сигнала, как было сказано ранее, равна 3,4 кГц. Частота дискретизации fд при fсигнала = 3,4 кГц долж­на удовлетворять условию fд, > 6800 имп/с. Принимается значение 8000 имп/с. Одна дискрета кодируется 8-разрядным кодом, поэтому скорость передачи информации на линейном участке должна составлять 8000x8 = 64 кбит/с. Это — скорость стандартного цифрового канала при им пульс но-кодовом методе модуляции (ИКМ).

Отметим, что искажения при малых амплитудах сигналов будут больше, чем при больших, поскольку независимо от амплитуды величина искажения Δ = q/2, т.е. равна половине шага квантования. Соответственно, искажение сигнала величиной в 1 квант составит 50 %, а для сигнала величиной в сто квантов относительное искажение будет в 100 раз меньше, т.е. 0,5 %.

Для реальных систем это свойство отрицательно влияет на качество речи, поскольку ис­кажает и без того слабые сигналы. Особенно это сказывается при междугородной связи, где на транзитных участках приходится много раз преобразовывать сигнал из цифровой формы в аналоговую и обратно. При этом слабые сигналы могут быть искажены до уровня шума. Выходом из этого положения является неравномерное кодирование или, как его еще назы­вают, компандирование.

Компандирование

Принцип командирования заключается в том, что диапазон значений амплитуды от максимального до минимального разбивается на сегменты. Те из них, которые соответству­ют меньшим значениям сигнала, квантуются более мелкими квантами, а для больших значе­ний выбираются большие кванты, величина которых возрастает с номером сегмента.

Используются два закона неравномерного кодирования: ц-компандирование и А-компандирование. Они имеют некоторые отличия, которые будут рассмотрены позднее. Нач­нем с компандирования по закону А.