Классическая выборка по количественным признакам

Классическая выборка по количественным признакам базируется на теории нормального распределения. Теория состоит в том, что, если из генеральной совокупности (например, платежных документов) последовательно произвести множество одинаковых по объему выборок, а по найденным средним суммам элементов каждой выборки построить частотное распределение, то вероятнее всего частота распределения сумм элементов окажется такой, как показано на рисунке.

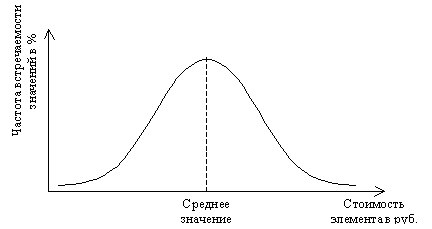
Подобное распределение называют нормальным. Как видно, такое распределение симметрично относительно среднего значения (в примере — средняя сумма платежного документа). Кроме того, кривая нормального распределения может быть описана математически и на основе этого становится возможным оценка результатов, полученных при статистическом выборочном исследовании.

Допустим, аудитор проверяет правильность начисления подоходного налога с сумм, выданных работникам крупного предприятия. Для этого он решает провести выборочное исследование: отобрать случайным образом 100 человек из 1200 работников предприятия и исследовать удержанный из их заработка подоходный налог. Проверка выявила 11 человек, из заработка которых подоходный налог был удержан не верно. Отклонение в начислении подоходного налога отражены в таблице 21.

Таблица 21 – Ошибки обнаруженные при проверке начисления налога с доходов физических лиц

Номер ошибки												Итого
Сумма ошибки			-400			-345				-780

Проводя исследование, аудитор хочет оценить недоплаченную в бюджет сумму налога, поэтому при подсчете итоговой суммы отклонений недоплаченные суммы налога компенсировались переплаченными. Для оценки полученных результатов необходимо:

1. Найти дисперсию выявленных отклонений:

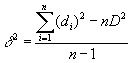, где

d ² — дисперсия;

i = 1, 2, …, n — порядковый номер элементов выборки, содержащих отклонения;

n — количество элементов выборки;

d_i — сумма выявленного отклонения i-того элемента;

D — среднее отклонение (определяется отношением суммарной величины отклонений к количеству элементов выборки; в примере D = 3201 : 100 = 32 руб.).

Дисперсия по данным примера составит:

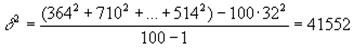
2. Найти среднюю ошибку выборки:

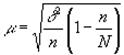, где

d ² — дисперсия (в примере — 41552);

n — количество элементов выборки;

N — количество элементов генеральной совокупности (в примере — 1200 человек).

По данным примера:

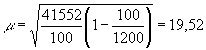(руб.)

3. Можно утверждать, что с вероятностью Р (%) суммарная величина отклонений в генеральной совокупности (S) лежит в пределах

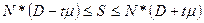, где

D — среднее отклонение (в примере 32 руб.);

m — средняя ошибка выборки (19,52);

t — коэффициент доверия для двухстороннего интервала. Берется аудитором из специальной таблицы в зависимости от выбранного им уровня уверенности (вероятности) Р (%) (т. е. от того, на сколько процентов аудитор хочет быть уверен в том, что величина отклонения, имеющаяся в генеральной совокупности, лежит в искомом интервале). Ниже представлен фрагмент таблицы коэффициентов доверия для двустороннего интервала

Уровень уверенности , %	Коэффициент доверия (для двухстороннего интервала) (t)
99,5	2,81
99,0	2,58
97,0	2,17
95,0	1,96
90,0	1,64
80,0	1,28

В Приложении 5 помещена полная таблица, по которой можно определить t, зная риск выборки (т. е. разницу между 100% и выбранным уровнем уверенности).

Пусть в примере аудитор выбрал уровень уверенности 95% (т. е. он допускает размер риска выборки 5% (100–95)). Тогда он может быть на 95% уверен, что общая сумма не начисленного подоходного налога по всем работникам предприятия (S) лежит в интервале

1200* (32–1,96* 19,52) < S < 1200* (32+1,96* 19,52)

-7511 руб. < S < 84311 руб.

Здесь переплата 7511 руб. является нижним пределом уверенности, а недоплата 84311 руб. — верхним пределом уверенности.

Схематически результат можно представить так:

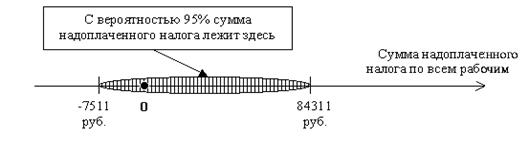
Возможно, аудитору необходимо узнать с определенной вероятностью Р (%) лишь верхний предел (в примере — максимальную величину возможной недоплаты).

Так, аудитор может быть на Р (%) уверен, что сумма недоплаты меньше 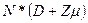, где Z — коэффициент доверия для одностороннего интервала. Данный коэффициент находится по таблице в зависимости от выбранного аудитором уровня уверенности Р (%). Фрагмент таблицы приведен ниже (полностью таблицу см. Приложение 6).

Уровень уверенности , %	Коэффициент доверия (для одностороннего интервала) (Z)
99,5	2,58
99,0	2,33
97,0	1,88
95,0	1,65
90,0	1,28
80,0	0,84

В рассматриваемом примере аудитор может быть на 95% уверен, что сумма недоплаченного подоходного налога по всем 1200 работникам предприятия не превышает 77050 руб.:

1200* (32+1,65*19,52) = 77050 руб.

Третий вариант — аудитора установил допустимую ошибку (максимальную сумму недоплаченного налога) в 65000 руб. и хочет подсчитать вероятность Р (%) того, что сумма недоплаченного налога по всем работникам не превысит данный предел (т. е. пункт б) наоборот).

Для этого необходимо найти Z по формуле

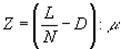, где

L — установленная аудитором предельная ошибка (в данном случае 65000 руб.);

а затем определить по таблице приложения 4 искомый уровень уверенности.

В примере:

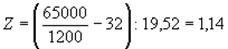
Для Z = 1,14 находим по таблице уровень уверенности равный 0,8729, или 87,3%. Значит, существует вероятность 13% (100%–87%) того, что сумма недоплаченного подоходного налога по генеральной совокупности превышает допустимый предел в 65000 руб. Если аудитор считает полученную вероятность ошибочного принятия допустимой, то дает положительное заключение по данному вопросу.

Коэффициент Z, рассчитываемый по последней формуле, может получиться отрицательным. Произойдет это в том случае, если средняя величина отклонения одного элемента по выборке больше установленной аудитором предельной величины. Знак "–" при коэффициента Z будет означать, что с найденной по таблице вероятностью Р (%) отклонение от нормы в генеральной совокупности превысит установленный предел (значит, вероятность того, что общая сумма отклонений не превысит установленный предел, составит лишь 100%–Р, но в любом случае меньше 50%).

Если средняя величина отклонения по выборке больше установленной аудитором в качестве допустимой ошибки, то вероятность того, что реально имеющиеся в генеральной совокупности ошибки превысят установленный предел, уже будет больше 50%.