Суммирующие и вычитающие устройства

Суммирующие устройства выполняют операцию описываемую уравнением вида:

y(t)= 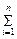а_iх_i(t), (2.3.)

где а_i – коэффициенты по каждому входу, а х_i – соответствующие входные переменные.

Для электрической цепи формула (2.3.) имеет вид:

y(t)= 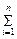K_iU_i(t), (2.4.)

где К_i – постоянные коэффициенты по каждому входу, а U_i – соответствующие входные электрические сигналы.

Несколько изменяемых во времени напряжений можно сложить с помощью параллельной или последовательной пассивных электрических цепей. Схема параллельной суммирующей цепи показана на рис. 2.5.1.

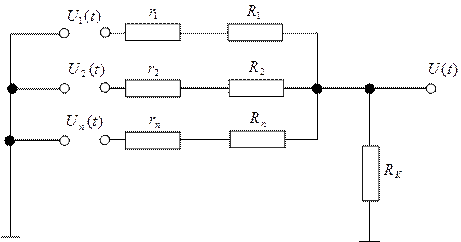Рис. 2.5.1. Параллельная пассивная суммирующая цепь

Здесь U₁ (t); U₂ (t);…; U_n (t) - независимые переменные входные сигналы; r₁ , r_{2 ,…,} r_n - внутренние сопротивления источников входных напряжений; R₁, R₂ ,…, R_n -резисторы, имеющие в общем случае разные номиналы сопротивлений R_н- собран после цепей. Реактивные элементы (конденсаторы и индуктивности) в пассивных цепях применяются реже, т.к. вносят дополнительную ошибку в виде сдвига фаз действующих напряжений и токов.

Для упрощения составления схемы обозначим проводимость соответствующей цепи нагрузки:

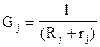и .

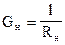В соответствии с законом Кирхгофа сумма токов, протекающих в параллельных цепях, равна току, протекающему через сопротивление нагрузки:

[U₁(t) - u(t)] G₁ + [U₂(t) - u(t)] G₂ + ... + [U_n(t) - u(t)] G_n = u(t) G_н ,

откуда

u(t) = 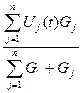. (2.5.)

Принимая проводимости всех цепей равными между собой (G₁ = G₂= ... = G_n = G) и коэффициент нагрузки схемы

,

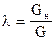запишем 2.5. в виде:

u(t) = 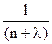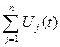= K 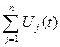, (2.6.)

где К = 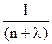- коэффициент передачи.

Схема последовательной суммирующей цепи показана на рисунке.

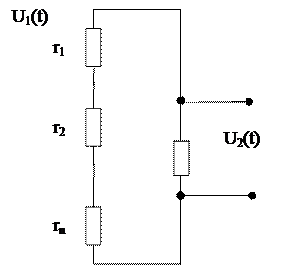Рис. 2.5.2. Последовательная пассивная суммирующая цепь

Ток, протекающий в цепи, равен:

,

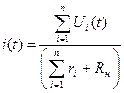где r_i – внутреннее сопротивление источников напряжения, а R_н – сопротивление нагрузки.

Выходное напряжение u(t), снимаемое с сопротивления нагрузки, можно выразить как

.

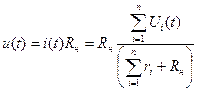Принимаем r₁=r₂=...=r и коэффициент нагрузки 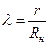, получим формулу, аналогичную (2.4.):

,

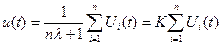где .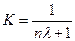

Пассивные цепи осуществляют операцию суммирования с точностью, определяемой погрешностью задания входных сигналов и погрешностью элементов схемы. Недостаток таких схем – зависимость результатов суммирования от числа слагаемых и сопротивления нагрузки, входящего в коэффициент. Это сильно ограничивает возможности варьирования коэффициентами передачи схемы по каждому входу. Поэтому пассивные суммирующие цепи применяют в неответственных вычислительных устройствах.

Активное суммирующее устройство. Суммирование электрических напряжений можно выполнить на основе операционного усилителя. При использовании в различных вычислительных устройствах ОУ охватывается глубокой отрицательной обратной связью, а на входе могут включаться различные функциональные элементы. Такие устройства получили название активных, так как используют операционный усилитель. На рис. 2.5.3. показана схема активного суммирующего устройства.

Рис. 2.5.3. Схема суммирующего усилителя

На рисунке и далее приняты следующие обозначения: U_i(t) - входные сигналы (напряжение); R_i - резисторы, стоящие на входе ОУ; R₀ - резисторы обратной связи; u(t) - выходное напряжение; U₀(t) -напряжение, действующее на входе ОУ, напряжение в суммирующей точке усилителя; i_вх - входной ток в усилитель; К_у - коэффициент усиления ОУ.

Для обеспечения нормальной работы решающего усилителя к ОУ предъявляется ряд требований:

· для снижения общей погрешности схемы он должен иметь большой коэффициент усиления К_у;

· для осуществления отрицательной обратной связи ОУ должен инвертировать знак входного напряжения;

· входные токи усилителя должны быть сведены к минимуму (i_вх»0);

· при нулевом входном сигнале напряжение на выходе ОУ должно быть равно нулю. В противном случае смещение или дрейф нуля выходного напряжения увеличивает общую погрешность схемы.

С учетом этих требований на основании закона Кирхгофа сумма токов, протекающих через входные резисторы R_i, равна току, протекающему через резистор обратной связи R₀:

.

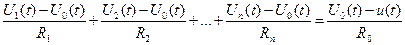Напряжение на выходе ОУ равно:

.

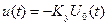Совместное решение обоих уравнений в результате исключения величины U₀(t) дает выражение для выходного напряжения схемы:

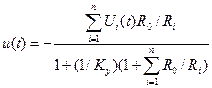. (2.7)

Так как К_у очень велик (для реальных усилителей он выбирается в пределах от нескольких десятков тысяч до нескольких миллионов), то при одинаковом порядке сопротивлений резисторов на входе и в обратной связи можно принять, что

.

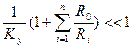Окончательная формула активного суммирующего устройства имеет вид:

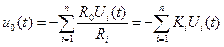, (2.8)

где u₀(t) - выходное напряжение идеального сумматора; K_i=R₀/R_i - коэффициент передачи суммирующего усилителя по i - му входу.

Формула (2.8.) показывает, что рассматриваемая схема удовлетворяет всем требованиям, предъявляемым к суммирующим цепям. Она имеет одинаковый изменяющийся в широких пределах диапазон входных и выходных напряжений, позволяет легко осуществлять вариацию передаточных коэффициентов изменением сопротивления входного резистора независимо по каждому входу. При этом знак выходного напряжения всегда противоположен знаку входного. В схеме, показанной на рис. 2.5.3., изменение коэффициента передачи по каждому входу осуществляется дискретно в соответствии с номинальными значениями резисторов R₀ и R_j. Плавное изменение коэффициента передачи производится в усилителе, построенном по схеме рис. 2.5.4. На входе резистора R_j поступает часть j входного напряжения e_j(t), снимаемого с потенциометра П_j. Формула (2.4.) для схемы с одним входом имеет вид:

u(t) = -(r₀/R_j) a_j U_j(t) = - K_j U_j(t), (2.9.)

где a_j - коэффициент, лежащий в пределах 0 < a_j <1.

Коэффициент передачи K_j = (r₀/R_j) a_j принимает любые значения в пределах от нуля до r₀/R_j в зависимости от значения a_j , т.е. от положения движка потенциометра.

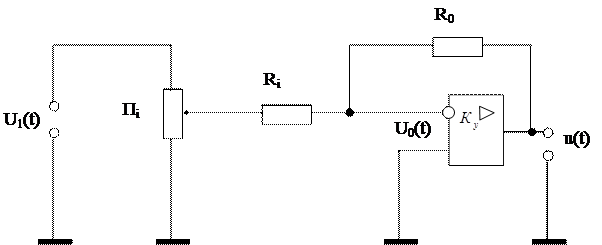
Рис. 2.5.4. Решающий усилитель с плавным изменением коэффициента передачи

Точность операции суммирования определяется погрешностями, возникающими из-за конечного значения коэффициента усиления ОУ, дрейфа нуля ОУ, неточностей изготовления резисторов, входного тока ОУ и динамическими погрешностями.

Погрешности от конечного значения коэффициента усиления ОУ. Выражение (2.7.) показывает, что чем больше коэффициент усиления К_у, тем с большей точностью схема, приведенная на рис. 2.5.4. выполняет операцию суммирования. Предельное значение коэффициента выбирается на основании заданной точности работы усилителя. Абсолютная погрешность схемы определяется разностью двух значений выходного напряжения - точного (2.7.) и приближенного - (2.8.).

D u_k(t) = u₀(t) - u(t), (2.10)

а относительная погрешность

du_k = D u_k / u₀, (2.11.)

После подстановки в (2.7.) формул (2.3.) и (2.4.) и преобразований получим:

du_k = 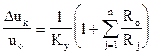. (2.12)

Одну из основных погрешностей работы решающего усилителя создает дрейф нуля ОУ. Это возникновение медленно меняющегося напряжения на выходе схемы усилителя при постоянном входном сигнале, в том числе и при входном напряжении, равном нулю. Он целиком обусловлен внутренними явлениями, протекающими в схеме ОУ. Оценку влияния дрейфа нуля усилителя на точность выходного напряжения ОУ рассмотрим на примере схемы, изображенной на рис. 2.5.4, предполагая для простоты, что j = 1. Тогда уравнение токов внешней цепи усилителя и уравнение усилителя имеет вид:

[U_j (t) - U_c (t)] / R_j = [U_c (t) - u (t)] / R_o. (2.13.)

u (t) = - K_у[U_c(t) ± U_др(t)],

где U_др - приведенный ко входу дрейф нуля. Это такое напряжение, которое следует подавать на вход усилителя в каждый данный момент, чтобы компенсировать погрешность в выходном напряжении.

В первое уравнение токов дрейф U_др(t) не входит, так как он действует только внутри принципиальной схемы ОУ. Совместно решая два последних уравнения и исключая U_c(t), получим выходное напряжение схемы:

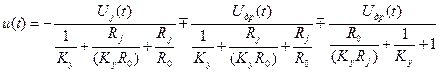
Имея в виду, что коэффициент усиления К_у имеет большое значение, пренебрегая в знаменателях членами, содержащими К_у, получим:

u (t) = - (R_o/R_j) U_j(t) (R_o/R_j) U_др(t) ± U_др(t) (2.14)

откуда, сравнивая с (2.9.), видно, что погрешность выходного напряжения от дрейфа нуля усилителя:

u_др(s) = ± (R_o/R_j) U_др(t) ± U_др(t). (2.15.)

Погрешность от неточностей изготовления резисторов. Погрешность выходного напряжения суммирующего усилителя в зависимости от отклонения сопротивления входных резисторов R_j и резистора обратной связи R_o от номинальных значений определяется по формуле:

Du_R(t) = - .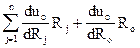

Принимая за основу формулу (2.8.) идеального суммирующего усилителя, получим:

u_R(t) = - 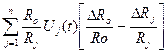. (2.16.)

Погрешность выходного напряжения схемы усилителя прямо пропорциональна первичным погрешностям резисторов, включенных на входе и в цепи обратной связи. Уменьшение этой погрешностей достигается постановкой прецизионных, как правило, проволочных резисторов, имеющих точность порядка 0,03-0,05 % при небольших значениях температурного коэффициента.

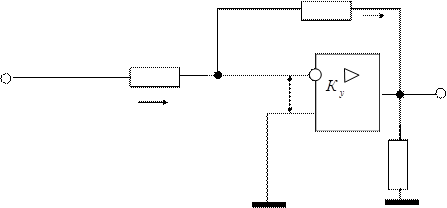
Инвертирующий усилитель. При анализе различных схем предположим, что входные токи по инверсному и неинверсному входам равны нулю. Следовательно, для схемы (рис. 2.5.5.), считая входной ток усилителя i_вх = 0,имеем I₁ = I₀ или U₁(t) / R₁ = - u (t) / R₀. Отсюда u (t) = - U₁(t) R₀ / R₁ = - Ke (t). Поскольку выходное напряжение имеет знак, противоположный входному, то такая схема называется инвертирующим усилителем.

R₀

I₀

R_j

U₁(t)

U₀»0

I₀ u(t)

R_н

Рис. 2.5.5. Схема дифференциального ОУ с заземленным

неинвентирующим входом

Инвертирующий сумматор. В практических схемах аналогичных устройств используется схема, в которой к инверсному входу дифференциального ОУ подсоединить несколько входных резисторов (рис. 2.5.6.). Образуется схема инвертирующего суммирующего усилителя - сумматора. Напряжение на инверсном входе u равно потенциалу земли. По закону Кирхгофа I₀ = I₁ = I₂ = ... = I_n. Поскольку I₀ = - u (t) / R₀; I₁ = U₁ (t) / R₁; I₂ = U₂ (t) / R₂ и т.д., то

u (t) = - [U₁ (t)R₀/R₁ + U₂ (t) R₀/ R₂ + ... + U_n (t) R₀/ R_n] или

u (t) = - K_jU_j(t), то есть получили формулу, аналогичную (2.8)

R₁ R₀

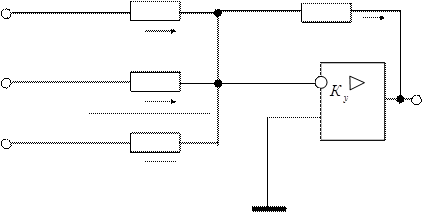U₁(t)

I₁ I₀

R₂ u^(-)

U₂(t)

I₂ U₀»0

R_n u(t)

U_n(t)

I_n

Рис. 2.5.6. Схема инвертирующего суммирующего усилителя

Неинвертирующий усилитель (рис. 2.5.7.). Напряжение на инверсном входе u^- = u (t) R₁ /(R₁ +R₀). Поскольку должно выполняться условие равенства сигналов на инверсном и неинверсном входах, т. е. e (t) = u и можно записать

u (t) = U (t) (I + R₀/R₁). (2.17)

Из полученного выражения видно, что происходит усиление входного напряжения без изменения знака с коэффициентом усиления

К = l + R₀/R₁. В частном случае, если R₀ = 0, то напряжение на выходе

u (t) = U (t), т. е. усилитель работает в режиме повторителя.

R₁ R₀

u ^-

u ⁺

u(t)

U(t)

Рис. 2.5.7. Схема неинвертирующего усилителя

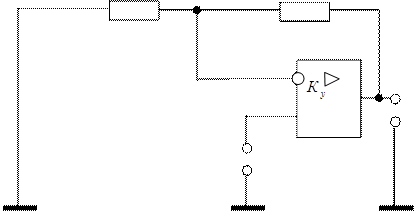
Неинвертирующий сумматор. (рис. 2.5.8.). Напряжение на инверсном и неинверсном входах равны, т.е.

u- = u⁺ = u (t) R_вх/ (R_вх + R₀). (2.18.)

Поскольку считаем, что неинвертирующий вход не потребляет тока, можно записать:

[[U₁ (t) - u⁺] / R₁ + U₂ (t) - u⁺] + ... + [U_n (t) - u⁺] / R_n = 0.

Поэтому:

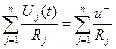. (2.19.)

Подставляя в (2.19.) равенство (2.18.) и решая относительно выходного напряжения, получим:

u (t) = 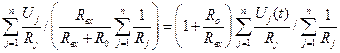. (2.20.)

Если сопротивление входных резисторов равны, т.е. R_i = R, то (2.20.) можно записать в виде:

u (t) = .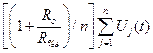

R_вх R₀

R₁ u^(-)

U₁(t)

R₂

U₂(t) U(t)

u⁽⁺⁾

U_n(t)

R_n

Рис. 2.5.8. Схема неинвертирующего сумматора

Сумматор-вычитатель. Схема, показанная на рис. 2.5.9. осуществляет вычитание сумм напряжений, подаваемых на инверсный и неинверсный входы ОУ.

При равенстве нулю входных токов усилителя для неинверсного входа в соответствии с законом Кирхгофа имеем:

.

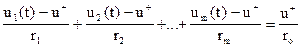После преобразований получим .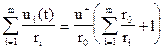

Для инверсного входа справедливо выражение:

.

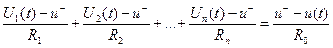Рис. 2.5.9. Схема сумматора-вычислителя на дифференциальном ОУ