Алгоритм вывода окружности

Для вывода контура окружности можно использовать соотношение между координатами X и Y для точек окружности X² + Y² = R²и построить алгоритм прямого вычисления коор­динат. Однако тогда необходимо вычислять квадратный корень, а это в цифровом компью­тере выполняется медленно.

Дадим запись инкрементного алгоритма Брезенхейма языком C++:

void Circle(int xc, int ус, int radius)

{

int x, у, dxt; long r2, dst, t, s, e, ca, cd, indx;

r2 = (long)radius*(long)radius;

dst = 4*r2;

dxt = (double)radius/1.414213562373;

t = 0;

s = -4*r2*(long)radius;

e = (-s/2) - 3*r2;

ca = -6*r2;

cd = -10*r2;

x = 0;

у = radius;

//Пиксел (xc, yc+radius);

//Пиксел (xc, ус-radius);

//Пиксел (xc+radius, yc);

//Пиксел (xc-radius, yc);

for (indx = 1; indx <= dxt; indx++)

{

x++;

if (e >= 0) e += t + ca;

else

{

y--;

е += t - s + cd;

s += dst;

}

t -= dst;

//Пиксел (xc+x, yc+y);

//Пиксел (xc+y, yc+x);

//Пиксел (xc+y, yc-x);

//Пиксел (xc+x, yc-y);

//Пиксел (xc-x, yc-y);

//Пиксел (xc-y, yc-x);

//Пиксел (xc-y, yc+x);

//Пиксел (xc-x, yc+y);

}

}

В этом алгоритме использована симметрия окружности — в основном цикле вычисля­ются координаты точек окружности только для одного октанта и сразу рисуются восемь симметрично расположенных пикселов.

Кривая Безье

Разработана математиком Пьером Безье. Кривые и поверхности Безье были использова­ны в 60-х годах компанией "Рено" для компьютерного проектирования формы кузовов ав­томобилей. В настоящее время они широко используются в компьютерной графике.

Кривые Безье описываются в параметрической форме: х = P_x(t), у = P_y(t).

Значение tвыступает как параметр, которому соответствуют координаты отдельной точ­ки линии. Параметрическая форма описания может быть удобнее для некоторых кривых, чем задание в виде функции у=f(x),поскольку функция f(x)может быть намного сложнее, чем P_x(t) и P_y(t), кроме того,f(х) может быть неоднозначной.

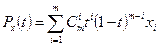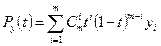Многочлены Безье для Р_х и Р_y имеют такой вид:

где х_iи у_i - координаты точек-ориентиров Р_i, а величины 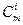- это известные из комбинато­рики, так называемые сочетания (они также известны как коэффициенты бинома Ньютона):

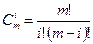
Значение т можно рассматривать и как степень полинома, и как значение, которое на I единицу меньше количества точек-ориентиров.

Рассмотрим кривые Безье, классифицируя их по значениям т.

т = 1 (по двум точкам)

Кривая вырождается в отрезок прямой линии, которая определяется конечными точками Р₀ и Р₁, как показано на рис. 72:

P(t) = (1- t)P₀ + t₁

т=2 (по трем точкам, рис. 73):

P(t) = (1- t)²P₀ + 2t(1- t)P₁ + t²P₂.

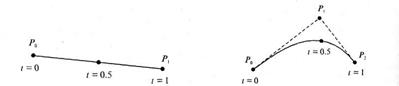
Рис. 72 Рис. 73

m - 3 (по четырем точкам, кубическая, рис 74). Используется довольно часто, в особенно­сти в сплайновых кривых:

P(t) = (1- t)³P₀ + 3t(1- t)²P₁ + 3 t²(1-t) P₂ + t³P₃.

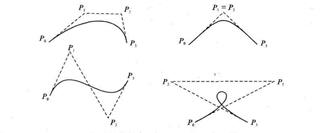
Рис. 74

Геометрический алгоритм для кривой Безье

Этот алгоритм позволяет вычислить координаты (х, у) точки кривой Безье по значению параметра t.

1. Каждая сторона контура многоугольника, который проходит по точкам-ориентирам, де­лится пропорционально значению t.

2. Точки деления соединяются отрезками прямых и образуют новый многоугольник. Коли­чество узлов нового контура на единицу меньше, чем количество узлов предшествую­щего контура.

3. Стороны нового контура снова делятся пропорционально значению t. И так далее. Это продолжается до тех пор, пока не будет получена единственная точка деления. Эта точка и будет точкой кривой Безье (рис. 75).

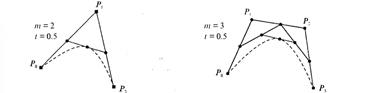
Рис. 75

Приведем запись геометрического алгоритма на языке C++:

for (i = 0; i <= m; i++)

R[i] = P[i]; //формируем вспомогательный массив R[ ]

for (j = m; j > 0; j --)

for ( i = 0; i < j; i++)

R[i] = R[i] + t * (R[i+1] - R[i]);

Отсечение отрезка

Необходимость отсечь выводимое изображение по границам некоторой области встречается довольно часто. В простейших ситуациях в качестве такой области, как правило, выступает прямоугольник.

Ниже рассматривается достаточно простой и эффективный алгоритм отсечения отрезков по границе произвольного прямоугольника. Он заключается в разбиении всей плоскости на 9 областей прямыми, образующими прямоугольник. В каждой из этих областей все точки по отношению к прямоугольнику расположены одинаково. Определив, в какие области попали концы рассматриваемого отрезка, легко понять, где именно необходимо отсечение. Для этого каждой области сообщается 4-битовый код.

4-битовый код:

- бит 0 означает, что точка лежит левее прямоугольника,

- бит 1 означает, что точка лежит выше прямоугольника,

- бит 2 означает, что точка лежит правее прямоугольника,

- бит 3 означает, что точка лежит ниже прямоугольника.