Лекция 3. Отображение геометрических объектов

Работа с компьютерной графикой требует от пользователя известной геометрической грамотности. Основы начертательной геометрии необходимы при разработке и выводе графической информации на экран монитора. Пространственное воображение, знание свойств аксонометрических проекций, правил построения перспективы облегчают работу с плоской и трехмерной графикой.

Геометрические соображения, подходы и идеи в соединении с постоянно расширяющимися возможностями компьютерной техники являются неиссякаемым источником существенных продвижений на пути машинной графики, ее эффективного использования в научных, конструкторских и художественных целях.

Основные понятия начертательной геометрии

Основными графическими объектами, которыми оперирует начертательная геометрия, являются точка, прямая, плоскость, поверхность.

Идеальная точка - объект, не имеющий измерений. Поэтому её считают нульмерной. Точки на чертеже обозначают прописными буквами латинского алфавита: A, B, C, D, E, F...

	Рис. 14. Обозначение точки на плоскости

Графически на плоскости точка задается декартовыми координатами – числами (x,y), однозначно определяющими местонахождение объекта. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x , y и z (абсцисса, ордината и аппликата).

	Рис. 15. Задание положения точки на плоскости

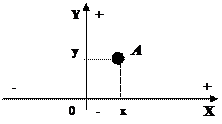Октант	I	II	III	IV	V	I	II	III
x	+	+	+	+	-	-	-	-
y	+	-	-	+	+	-	-	+
z	+	+	-	-	+	+	-	-

Плоскости проекций, попарно пересекаясь, определяют три оси 0x, 0y и 0z, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0. Три плоскости проекций делят пространство на восемь трехгранных углов - октантов.

Таблица 3.1.

Знаки координат в октантах

В современной математике точкой называют элементы весьма различной природы, из которых состоят различные пространства (например, в n-мерном евклидовом пространстве точкой называют упорядоченную совокупность из n- чисел).

В зависимости от поставленной задачи точкой может быть молекула, город на карте, звезда во Вселенной.

Прямая линия.Если основой построения в геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим.

Прямая линия в линейной алгебре - линия первого порядка на плоскости. Общее уравнение прямой:

Ах+Ву+С=0,

где А, В и С - любые постоянные.

Линии на чертежах обозначают строчными буквами латинского алфавита: a, b, c, d, e, f ...

Для определения положения прямой в пространстве существуют следующие методы: