Метод минимальных путей и минимальных сечений
Метод минимальных путей и минимальных сечений является приближенным и позволяет дать оценку минимальным и максимальным значением вероятности безотказной работы. Этот метод обычно используется в случае, если необходимо получить результаты в виде аналитического выражения.
Определим основные понятия. Если F(x)=1 и F(y)=0 при любых y<x, то x-логический вектор, определяющий минимальный путь. Характерной особенностью минимального пути является то, что отказ хотя бы одного элемента пути (если работоспособны только элементы пути) влечет за собой отказ всей сети.
Если F(x)=0 и F(y)=1 при любых y>x, то x - логический вектор, определяющий минимальное сечение, т.е. каждое минимальное сечение состоит из минимальной совокупности подсистем, одновременный отказ которых влечет за собой отказ всей сети. Особенность минимального сечения состоит в том, что восстановление хотя бы одного элемента в сечении влечет восстановление всей сети.
По данному методу можно получить вероятность безотказной работы в виде двойного неравенства:
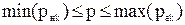 . (5)
. (5)
Вероятность 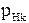 выражается как вероятность безотказной работы вспомогательной системы, составленной из последовательно включенных групп подсистем, соответствующих всем минимальным сечениям сети:
выражается как вероятность безотказной работы вспомогательной системы, составленной из последовательно включенных групп подсистем, соответствующих всем минимальным сечениям сети:
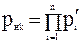 , (6)
, (6)
где n - общее количество минимальных сечений для k-й пары узлов; 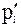 - вероятность безотказной работы i-го минимального сечения, определяемая следующим образом:
- вероятность безотказной работы i-го минимального сечения, определяемая следующим образом:
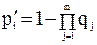 , (7)
, (7)
где m - число составляющих элементов в i-м минимальном сечении; 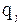 - вероятность отказа j-го элемента в i-м сечении.
- вероятность отказа j-го элемента в i-м сечении.
Вероятность 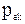 выражается как вероятность безотказной работы вспомогательной системы, составленной из параллельно включенных групп подсистем, соответствующих всем минимальным путям сети, т.е.
выражается как вероятность безотказной работы вспомогательной системы, составленной из параллельно включенных групп подсистем, соответствующих всем минимальным путям сети, т.е.
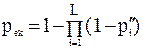 , (8)
, (8)
где L - число минимальных путей, соединяющих k-ю пару узлов; 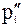 - вероятность безотказной работы i-го пути:
- вероятность безотказной работы i-го пути:
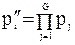 , (9)
, (9)
где G - количество элементов в i-м минимальном пути.
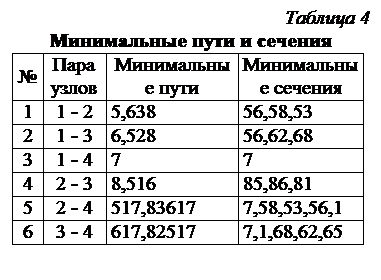 Данный метод позволяет свести анализ сетей к анализу систем с последовательно-параллельной структурой, и поэтому может быть использован для сетей с достаточно сложной конфигурацией.
Данный метод позволяет свести анализ сетей к анализу систем с последовательно-параллельной структурой, и поэтому может быть использован для сетей с достаточно сложной конфигурацией.
Пример 2
Оценим надежность сети, представленной на рис. 26, где в качестве исходных данных взяты исходные данные из примера 1. Для этого выделим все минимальные сечения и пути для каждой пары узлов (табл. 4).
Запишем, в соответствии с (6)-(9), выражения для вычисления нижней и верхней границы вероятности безотказной работы (для каждой пары узлов):
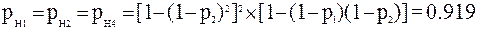 ;
;
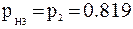 ;
;
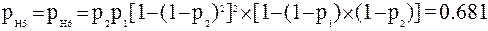 =min(
=min( 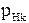 );
);
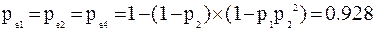 =max(
=max( 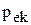 );
);
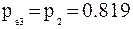 ;
;
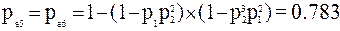 .
.
Таким образом, в соответствии с (5), можно записать, что вероятность безотказной работы системы находится в диапазоне:
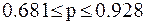 .
.
