Размещения с повторениями и без повторений

Симметрическая разность.

A D B:= (A \ B) И (B \ A) = (A И B) \ (A З B)

Свойства операций над множествами.

1. Коммутативность.

A И B=B И A
A З B=B З A

1. Ассоциативность.

(A И B) И C=A И (B И C)
(A З B) З C= A З (B З C)

1. Дистрибутивность.

(A И B) З C = (A З C) И (B З C)
(A З B) И C= (A И C) З (B И C)

1. A И A=A, A З A=A
   A И Ж = A, A З Ж= Ж
2. Законы де Моргана (законы двойственности).

1) A И B= A З B
2) A З B= A И B

28.Мощьность множества. Декартово произведение.

Мощность множества, кардинальное число— характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.

Прямое или декартово произведение двух множеств — это множество, элементами которого являются всевозможные упорядоченные пары элементов исходных множеств.

29.Наглядное представление задаваемых множеств. Диаграмма Эйлера-Венна.

Диаграмма Венна (иногда диаграмма Эйлера — Венна) — схематичное изображение всех возможных пересечений нескольких (часто — трёх) множеств

30.Упорядоченные и неупорядоченные выборки.

Выборками называются подмножества какого-либо множества.

Упорядоченными выборками называются выборки, в которых важен порядок элементов.

Если в выборке поменяют местами два элемента и получится другая выборка, то данная выборка является упорядоченной.

Неупорядоченными выборками называются выборки, в которых не важен порядок элементов.

Размещения с повторениями и без повторений.

Размещение с повторениями или выборка с возвращение — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз.

32.Сочитания с повторениями и без повторений.

Сочетаниями без повторений из n различных элементов по k элементов называются комбинации, которые составлены из данных n элементов по k элементов и отличаются хотя бы одним элементом .

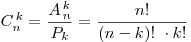
Пусть имеются предметы n различных видов предметов, и из них составляются наборы, содержащие k элементов. Такие выборки называются сочетаниями с повторением.

.

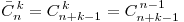33. перестановки с повторениями и циклические перестановки.

Всякое размещение с повторениями, в котором элемент 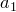повторяется раз, элемент 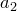повторяется 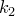раз и т.д. элемент 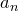повторяется 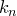раз, где , , 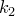, 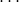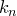— данные числа, называется перестановкой с повторениями порядка

Определение циклической перестановки. Пусть a1; a2; : : : ; ak — попар-

но различные элементы Xn. Перестановку ', действующую по правилу

'(a1) = a2; '(a2) = a3; : : : ; '(ak) = a1;

'(j) = j при j =2 fa1; a2; : : : ; akg;

называют циклической перестановкой элементов a1; a2; : : : ; ak или циклом

из элементов a1; a2; : : : ; ak. Обозначение:

' = (a1 a2 : : : ak)n.

34.Основные понятия теории графов: вершины, ребра, инцидентность, смежность.

Вершина — верхняя точка чего-либо.

Ребро — любой отрезок, являющийся стороной какого-либо многогранника

Матрица смежности — один из способов представления графа в виде матрицы. это квадратная матрица размерностью n x n, (где n – число вершин графа ), однозначно представляющая его структуру.

ИНЦИДЕНТНОСТЬ — геометрический термин, употребляемый для обозначения отношения принадлежности (связи, соединения) между основными объектами геометрии: точками, прямыми, плоскостями. Свойства И. характеризуются так наз. аксиомами принадлежности

Матрица инцидентности представляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m– количество дуг графа.

35.Типы графов: элементарный граф, граф с петлями, мультиграф, псевдограф, орграф.

Определение: (p,q) – граф, есть система объектов. G=(V,E), где V={v₁, v₂,…,v_p} – множество вершин, E={ e₁=(v_i1,v_j1), e₂=(v_i2,v_j2),…, e_q=(v_iq,v_jq)}i_k ≠ j_k k=1,2,3,..,q – множество неориентированных ребер i_k≠j₁, k=1..q.Мультиграф допускает кратные ребра, но не допускает петель. Песевдограф допускает и кратные ребра, и петли.

Петля это дуга, начальная и конечная вершина которой совпадают.

мультиграф, у которых две вершины могут быть соединены двумя и более рёбрами.

36.Связанные и несвязанные графы. Компоненты связанности.

Неориентированный граф считается связным, если из любой вершины есть путь в любую другую вершину (путь может состоять из любого количества рёбер).

Граф считается не связанным, если из одной вершины нельзя будет провести ни в какую другую вершину.

Компонента связности - множество вершин такое, что из любой вершину этого множества есть путь в любую другую вершину этого множества, но ни из какой вершины этого множества нельзя попасть в некоторую вершину вне этого множества.

37.Способы описания графов.

Граф описывается перечислением множества вершин и дуг.

38. Способы задания множеств. Понятие мощность множества.

Считают, что множество задано своими элементами, т.е. множество задано, если о любом объекте можно сказать: принадлежит он этому множеству или не принадлежит. Задавать множество можно следующими способами:

1) Если множество конечно, то его можно задать перечислением всех его элементов.

2) Множество можно задать указанием характеристического свойства его элементов. Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий ему.

Мощность множества или кардинальное число множества — это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные.

42. Операции над подстановками.

подстановка — это операция синтаксической замены подтермов данного терма другими термами, согласно определённым правилам.