Теория булевых функций. Булева алгебра
Определение. Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией (*) и двумя выделенными элементами называется булевой алгеброй, если выполнены следующие свойства (аксиомы булевой алгебры). Названия операций пока не введены.
1. X & Y = Y&X, X V Y = Y V X – коммутативность.
2. (X & Y) & Z = X & (Y & Z), (X V Y) V Z = X V (Y V Z) – ассоциативность.
3. (X V Y) & Z = (X & Z) V (Y & Z), (X & Y) V (Y & Z) = (X V Z) & (Y & Z) – дистрибутивность.
4. Поглощение – X & X = X, X V X = X.
5. Свойства констант X & 0 = 0 X & I = X, где I – аналог универсального множества.
6. Инвальтивность (X*)* = X
7. Дополнимость X V X* = I, X & X* = 0.
8. Законы двойственности – (X & Y)* = X* V Y*, (X V Y)* = X* & Y
Булева алгебра всех подмножеств данного множества.
U = {a1, a2… an) [U] = N [P(U)] = 2n
Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.
Oбъединение эквивалентно V, пересечение - &, дополнение - *, пустое множество – 0, а универсальное – I.
Все аксиомы булевой алгебры справедливы в операциях над множествами.
Булева алгебра характеристических векторов.
Пусть A <= U, A <- P(U) ? - характеристический вектор этого подмножества.
?A = {?1, ?2 ..?n) n = [P(U)]
?i = 1, если ai <- A (принадлежит).
?i = 0, если ai не принадлежит A.
U = {1 2 3 4 5 6 7 8 9} A = {2 4 6 8} B = {1 2 7}
?A = {0 1 0 1 0 1 0 1 0} ?B = {1 1 0 0 0 0 1 0 0} или
?A = 010101010 – скобки не нужны ?A= 110000100
Характеристические векторы размерностью n называются булевыми векторами. Они располагаются в вершинах n – мерного булева куба. Номером булевого вектора является число в двоичном представлении, которым он является
1101 – номер.
Два булевых вектора называются соседними, если их координаты отличаются только в одном разряде (если они отличаются только одной координатой). Совокупность всех булевых векторов размерности n называется булевым кубом размерностью Bn.
0 – нулевой вектор. I – вектор из одних единиц.
|XY |X&Y |X V Y |
|00 |0 |0 |
|01 |0 |1 |
|10 |0 |1 |
|11 |1 |1 |
Отрицание X = 0 Y = 0 Х = 1 Y= 1
Для размерности n операции над векторами производятся по координатно. Логическая сумма двух векторов – вектор, координаты которого являются логическими суммами соответствующих исходных векторов. Аналогично определено произведение.
Утверждение Между множеством всех подмножеств множества U и булевым кубом Bn, где n= =[U] можно становить взаимное соответствие, при котором операции объединения множества соответствует операции логического сложения (их характеристических векторов), операции пересечения множеств соответствует операция логического умножения их характеристических векторов, а операции дополнения – операция отрицания. Пустому множеству соответствует нулевой вектор, а универсальному – единичный.
Следствие Множество всех характеристических векторов является булевой алгеброй.
Булева алгебра высказываний (алгебра логики)
Высказыванием об элементах множества U называется любое утверждение об элементах множества U, которое для каждого элемента либо истинно, либо ложно.
U = {1 2 3 4 5 6 7 8 9}
A = «число четное» B = «число, меньшее пяти»
Множеством истинности высказывания называется совокупность всех элементов, для которых это высказывание истинно.
SA = {2 4 6 8} SB = {1 2 3 4}
Высказывание, для которого множество истинности пусто, называется тождественно ложным, а для которого SB = U называется тождественно истинным.
Высказывания, для которых множества истинности совпадают, называются тождественными или равносильными. Равносильные высказывания объединим в один класс Р.В. и не будем их разделять, т.к. все они имеют одно и то же множество истинности.
Операции над высказываниями
Дизъюнкция высказываний (V, ИЛИ, OR). Дизъюнкция высказываний – высказывание, истинное тогда, когда истинно хотя бы одно из высказываний.
Конъюнкция высказываний (&, И, AND). Конъюнкцией высказываний называется высказывание, истинное тогда и только тогда, когда истинны все высказывания.
Отрицание высказываний (- над буквой, НЕ, NOT). Отрицанием высказывания называется высказывание, истинное только тогда, когда исходное высказывание ложно.
|A B |A & B A V B |Not A |
|Л Л |Л |Л |И |
|Л И |Л |И И |
|И Л |Л |И |Л |
|И И |И |И |Л |
Л – ложно.
И – истинно.
Утверждение (основа всей алгебры логики) Между множеством всех классов эквивалентных высказываний об элементах множества U и множеством P(U) можно установить взаимно однозначное соответствие, при котором операция дизъюнкции высказываний соответствует
операции объединения множеств истинности, а конъюнкция соответствует операции пересечения. Операция отрицания соответствует операции дополнения.
Следствие. Множество классов эквивалентных высказываний является булевой алгеброй.
Теорема Существуют 3 булевых алгебры: 1. P(U) 2. Bn 3. Множество классов эквивалентных высказываний. Три булевых алгебры являются изоморфными, если между их элементами можно установить такое однозначное соответствие, при котором операции сохраняются.
Договоримся конъюнкцию обозначать точкой (как знак умножения в алгебре чисел). Конъюнкция выполняется раньше дизъюнкции (аналог выполнения операций сложения и умножения в алгебре чисел).
Тема 4. Основы дискретной математики
Понятие графа
Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. С дворянским титулом «граф» их связывает общее происхождение от латинского слова «графио» - пишу.
В математике определение графа дается так:
Графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами.
Примерами графов могут служить схемы авиалиний, метро, дорог, электросхемы, чертежи многоугольников. Использует графы и дворянство. Например, в генеалогическом дереве, вершины – члены рода, а связывающие их отрезки – отношения родственности. Использует графы и дворянство. На рисунке приведена часть генеалогического дерева знаменитого дворянского рода. Здесь его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям.

Слово «дерево» в теории графов означает граф, в котором нет циклов, то есть в котором нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину. Генеалогическое дерево будет деревом и в смысле теории графов, если в этом семействе не было браков между родственниками.
Первая работа по теории графов принадлежит Леонарду Эйлеру (1736 год), хотя термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг.

С помощью графов часто упрощалось решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. Помогают графы в решении математических и экономических задач.
Схема графа, состоящая из «изолированных» вершин, называется нулевым графом. (рис.2)
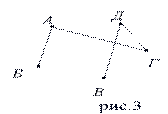
Графы, в которых не построены все возможные ребра, называются неполными графами. (рис.3)
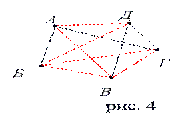
Графы, в которых построены все возможные ребра, называются полными графами. (рис.4)
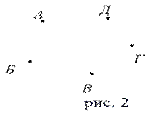
Если на ребрах графа нанесены стрелочки, указывающие направление ребер, то такой граф называют направленным.
Стрелка от одой работы к другой на графе, изображенном на рисунке, означает последовательность выполнения работ. Нельзя начинать монтаж стен, не закончив строить фундамент, чтобы приступить к отделке, нужно иметь на этажах воду и т. д.
2. Степени вершин и подсчет числа ребер.
Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной.
Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный.

рис.5
На рисунке 5 изображен граф с пятью вершинами. Степень вершины А обозначим Ст.А.
На рисунке: Ст.А = 1, Ст.Б = 2, Ст.В = 3, Ст.Г= 2, Ст.Д= 0.
Сформулируем некоторые закономерности, присущие определенным графам.
Закономерность 1. Степени вершин полного графа одинаковы, и каждая из них на 1 меньше числа вершин этого графа.
Доказательство:
Эта закономерность очевидна уже после рассмотрения любого полного графа. Каждая вершина соединена ребром с каждой вершиной, кроме самой себя, т. е. из каждой вершины графа, имеющего n вершин, исходит n—1 ребро, что и требовалось доказать.
Закономерность 2. Сумма степеней вершин графа число четное, равное удвоенному числу ребер графа. Эта закономерность справедлива не только для полного, но и для любого графа.
Доказательство:
Действительно, каждое ребро графа связывает две вершины. Значит, если будем складывать число степеней всех вершин графа, то получим удвоенное число ребер 2R (R — число ребер графа), т. к. каждое ребро было подсчитано дважды, что и требовалось доказать.
ТЕОРЕМА. Число нечетных вершин любого графа четно.
Доказательство:
Рассмотрим произвольный граф Г. Пусть в этом графе число вершин, степень которых 1, равна К1; число вершин, степень которых 2, равно K2; ...; число вершин, степень которых n, равно Кn. Тогда сумму степеней вершин этого графа можно записать как K1 + 2К2 + ЗК3 + ...+ nКn. С другой стороны: если число ребер графа R, то из закономерности 2 известно, что сумма степеней всех вершин графа равна 2R. Тогда можно записать равенство K1 + 2К2 + ЗК3 + ... + nКn = 2R. (1) Выделим в левой части равенства сумму, равную числу нечетных вершин графа (К1 + К3 + ...):K1 + 2К2 + ЗК3 +К4 + 5К5 + ... + nК = 2R, (К1 + К3 + К5 +...) + (2K2 + 2Х3 +4K4 + 4К5 + ...)=2R Вторая скобка- четное число как сумма четных чисел. Полученная сумма (2R) четное число. Отсюда (К1 + К3 + К5 +...)-четное число. Заметим, что если полный граф имеет n вершин, то количество ребер будет равно n(n-1)/2
Действительно, количество ребер в полном графе с n вершинами определяется как число неупорядоченных пар, составленных из всех n точек-ребер графа, т. е. как число сочетаний из n элементов по 2:
Граф, не являющийся полным, можно дополнить до полного с теми же вершинами, добавив недостающие ребра. Так, например, на рисунке 3 изображен неполный граф с пятью вершинами. На рисунке 4 ребра превращающие граф в полный граф изображены другим цветом, совокупность вершин графа с этими ребрами называется дополнением графа.
Эйлеровы графы.
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. (рис.6)
Такими графы названы в честь учёного Леонарда Эйлера.
Закономерность 3 (вытекает из рассмотренной намитеоремы). Невозможно начертить граф с нечетным числом нечетных вершин.
Закономерность 4. Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.
Закономерность 5. Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.
Закономерность 6. Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
