Обобщенная линейная модель множественной регрессии (ОЛММР) и обобщенный МНК
Коренное отличие обобщенной модели от классической состоит только в виде ковариационной квадратной матрицы вектора возмущений: вместо матрицы Σε = σ2En для классической модели имеем матрицу Σε = Ω для обобщенной. Последняя имеет произвольные значения ковариаций и дисперсий. Формально обобщенная линейная модель множественной регрессии (ОЛММР) в матричной форме имеет вид: Y = Xβ + ε (1) и описывается системой условий:
1. ε – случайный вектор возмущений с размерностью n; X -неслучайная матрица значений объясняющих переменных (матрица плана) с размерностью nх(р+1); напомним, что 1-й столбец этой матрицы состоит из единиц; 2. M(ε) = 0n – математическое ожидание вектора возмущений равно ноль-вектору; 3. Σε = M(εε’) = Ω, где Ω – положительно определенная квадратная матрица; заметим, что произведение векторов ε‘ε дает скаляр, а произведение векторов εε’ дает матрицу размерностью nxn; 4. Ранг матрицы X равен р+1, который меньше n; напомним, что р+1 - число объясняющих переменных в модели (вместе с фиктивной переменной), n - число наблюдений за результирующей и объясняющими переменными.
Сравнивая обобщ. модель с класс., можно сказать, что она отличается от класс. только видом ковар. матр.: вместо 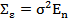 для класс. модели имеем
для класс. модели имеем 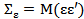 =Ω для обобщенной. Это означ., что в отличие от класс., в обобщенной модели ковариации и дисперсии объясняющих переменных м.б. произвольными. В этом состоит суть обобщения регрессионной модели.
=Ω для обобщенной. Это означ., что в отличие от класс., в обобщенной модели ковариации и дисперсии объясняющих переменных м.б. произвольными. В этом состоит суть обобщения регрессионной модели.
Следствие 1. Оценка парам-в модели (1) обыч МНК: b = (X’X)-1X’Y (2) является несмещенной и состоятельной, но неэффективной (неоптимальной в смысле теоремы Гаусса-Маркова). Для получения эфф-й оценки нужно использовать обобщенный метод наименьших квадратов. . Однако формула для ковариационной матрицы вектора оценок Σb оказывается неприемлемой в условиях обобщенной модели.
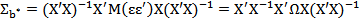 в то время как для классической модели
в то время как для классической модели 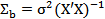 . Эта оценка для обобщ. модели явл. смещенной (и неэффективной
. Эта оценка для обобщ. модели явл. смещенной (и неэффективной
Найдем мат. ожидание остаточной суммы квадратов 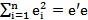 , используя преобразования можно показать, что для обобщенной модели
, используя преобразования можно показать, что для обобщенной модели 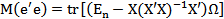
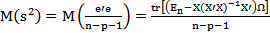 где символ tr означает след соответствующей матрицы. Следовательно, если в качестве оценки ковар. матр. Σb заменить σ2 на s2, т.е. взять матрицу
где символ tr означает след соответствующей матрицы. Следовательно, если в качестве оценки ковар. матр. Σb заменить σ2 на s2, т.е. взять матрицу 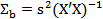 , то ее мат.ожидание
, то ее мат.ожидание
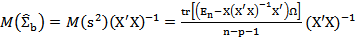
Это означает, что обычный МНК в обобщ. лин. регресс. модели дает смещенную оценку ковар. матрицы Σb вектора оценок b
Для получения наиболее эффективной оценки нужно использовать другую оценку, получаемую так называемым обобщенным методом наименьших квадратов.
Вопрос об эфф-ти лин. несмещенной оценки вектора β для обобщ. регресс. модели решается с помощью следующей теоремы.
Теорема Айткена. В классе линейных несмещенных оценок вектора β для обобщенной регрессионной модели оценка 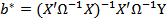 имеет наименьшую ковариационную матрицу. Свойства оценок 1)Оценка обобщенного метода наименьших квадратов b* совпадает с оценкой «обычного» метода b.2)При выполнении предпосылки о нормальном законе распределения вектора возмущений ε можно убедиться в том, что оценка b* обобщ. МНК для параметра β при известной матрице Ω совпадает с его оценкой полученной методом максимального правдоподобия; 3)Оценка b* обобщенного МНК может быть определена как точка минимума обобщенного критерия e'Ω-1e.
имеет наименьшую ковариационную матрицу. Свойства оценок 1)Оценка обобщенного метода наименьших квадратов b* совпадает с оценкой «обычного» метода b.2)При выполнении предпосылки о нормальном законе распределения вектора возмущений ε можно убедиться в том, что оценка b* обобщ. МНК для параметра β при известной матрице Ω совпадает с его оценкой полученной методом максимального правдоподобия; 3)Оценка b* обобщенного МНК может быть определена как точка минимума обобщенного критерия e'Ω-1e.
