Этапы решения задачи на компьютере
Перед нами может стоять задача, для решения которой на компьютере уже имеется готовая программа. Если у нас есть право на ее использование, то мы можем применить эту программу. Так, для работы с текстом, графическим изображением, для типовых расчетов все чаще используют разработанное специалистами прикладное программное обеспечение. Но если для решения задачи хотят прибегнуть к помощи компьютера, а готовой программы для ее решения нет, то понадобится освоить весь процесс решения задачи на компьютере, создав свою оригинальную (уникальную) программу.
В этом случае процесс решения задачи на компьютере включает в себя следующие основные этапы:
1. Постановка задачи.
2. Выбор метода решения (построение математической модели).
3. Разработка алгоритма.
4. Составление программы.
5. Реализация программы на компьютере.
6. Анализ полученных результатов.
Постановка задачи. Чтобы выбрать метод решения, разработать математическую модель, необходимо четко представлять, чем мы располагаем – какие есть исходные данные, каковы ограничения на них. И, конечно же, никакую задачу нельзя решить, если не понимать, что будет являться решением задачи, что должно стать результатом всего процесса решения. На эти вопросы может помочь ответить правильная постановка задачи. Так, если задача конкретная (например, надо решить уравнение 2х2+3х+5=0, где коэффициенты уравнения - константы), то под постановкой задачи понимаем ответ на вопросы:
какие исходные данные известны;
что требуется определить.
Если задача обобщенная (например, надо решить квадратное уравнение ax2 + bx + c = 0), то отвечать при постановке задачи понадобится еще на третий вопрос: какие данные допустимы. Итак, постановка задачи "решить квадратное уравнение ax2 + bx + c = 0" выглядит следующим образом:
Дано: a, b, c - коэффициенты уравнения.
Требуется: x1, x2 - корни у равнения.
Ограничения: a<>0 и D=b2–4ac>=0
Таким образом, мы указали ограничения на значения исходных данных и на их соотношение, а также задали математическое соотношение – формулу, связывающую переменные, значения которых должны быть даны, с теми переменными, значения которых ищем. Следовательно, указывая такие связи при постановке задачи, мы задаем метод решения квадратного уравнения, формализуя его.
Выбор метода решения (построение математической модели). Разрабатывать алгоритм как последовательность действий будущего исполнителя, направленных на решение задачи, можно лишь тогда, когда ясно, как решать задачу, в чем ее смысл, сложность, к какому классу задач она принадлежит, какой способ, метод решения наиболее адекватно будет соответствовать реальным явлениям и процессам. Таким образом, речь идет о выборе метода решения в простейшем случае и о построении математической модели реальной задачи в более сложной ситуации. Действительно, компьютер решает задачу, выполняя команды нашего алгоритма, выраженные на языке программирования. Но мы знаем, какой вид приняли эти команды, попав в память компьютера: они имеют вид электрических сигналов, соответствующих двоичному способу кодирования. Обработка этих сигналов, выполнение требуемых операций происходит в компьютере по законам алгебры логики и двоичной системы счисления. Это возможно, если все действия, необходимые для решения задачи, формализованы, то есть, представлены как математические операции и соотношения между входящими в них переменными. В случае большого числа параметров, ограничений, возможных вариантов исходных данных модель явления может иметь очень сложное математическое описание (правда, реальное явление еще более сложно), но если такого описания не будет, то переложить решение задачи на компьютер вряд ли удастся. Поэтому часто построение математической модели требует упрощения требований задачи, отказа от некоторых ограничений. А для решения квадратного уравнения, когда необходимо получить значения его корней (если они есть), мы можем воспользоваться известными из курса алгебры формулами. На уроках математики доказывалась правильность метода решения квадратного уравнения путем вычисления по формулам x1= 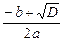 , x2=
, x2= 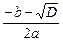
Нам уже известно, что этот метод решения дает искомые значения корней при любых допустимых значениях исходных данных - коэффициентов А, В, С. Поэтому мы строим алгоритм, основываясь на этом методе решения.
Разработка алгоритма. В основу программы для компьютера кладется алгоритм решения данной задачи, то есть система точных и понятных предписаний (команд) о последовательности действий, позволяющая за конечное число их шагов получить результат. Этап алгоритмизации заслуженно считается наиболее творческим, но и самым трудным. Алгоритм отражает всю логику наших рассуждений при решении задачи, но обязательно учитывает, что исполнителем алгоритма мы выбрали компьютер – автомат с определенным набором возможностей и устройств для выполнения команд. Поэтому алгоритм, разрабатываемый нами с ориентацией на компьютер как на исполнитель, должен обладать свойствами дискретности, понятности, детерминированности, результативности и массовости. Алгоритм составляется в форме, допустимой для конкретного типа алгоритма, чаще всего в графической, ввиду универсальности ее применения и наглядности.
Составление программы. Компьютер может многое, однако это всего лишь автомат, хотя и совершенный. Он решает задачи, быстро и точно выполняя команды. Эти команды должны предоставить компьютеру человек. Последовательность команд составляет хранимую в памяти компьютера программу. Современную компьютерную программу решения определенного класса задач программист пишет на языке программирования и затем, как говорят, реализует на компьютере.
Реализация программы на компьютере. Это значит, что текст программы вводят с клавиатуры в оперативную память и проводят ее отладку. Отладка компьютерной программы означает не только устранение синтаксических ошибок, в поиске которых помогает транслятор. Также должна обязательно производиться проверка работы программы на конкретных вариантах исходных данных, подобранных так, чтобы охватить все возможные для данной задачи случаи. Например, если это программа решения квадратного уравнения, то нужно проверить ее работоспособность как для варианта значений коэффициентов a, b, c, при которых дискриминант D>0, так и при таком варианте a, b, c, когда D < 0. Отметим, что здесь речь идет о проверке именно работоспособности программы. Это означает проверку возможности работы всех ее альтернативных ветвей от начальной команды программы до предусмотренного условием задачи выхода из программы (остановки), в том числе проверку отсутствия неправильной организации циклов (в частности, зацикливания).
Анализ полученных результатов. Анализируя получаемые результаты такого контрольного расчета, в случае их правильности можно сделать вывод о правильности всех предшествующих программированию этапов. Как же определить, что результаты получены правильные? Для этого в зависимости от класса решаемой задачи применяют разные подходы:
сравнивают полученные результаты с результатом, рассчитанным в соответствии с тем же методом, но вручную или с помощью калькулятора. Для приведенного выше примера это означает сравнение значений корней квадратного уравнения, полученных при компьютерном расчете, со значениями тех же корней, предварительно рассчитанных вручную. Условием правомерности такого сравнения является расчет этих значений в обоих случаях одним и тем же методом и при одинаковых наборах значений коэффициентов уравнения. Для предварительных расчетов вручную обычно подбирают исходные значения, облегчающие их проведение. Так, для коэффициентов a, b и c в случае различных действительных корней удобными являются соответственно значения 1; 3; -4, для случая двух действительных совпадающих корней - значения 1; 2; 1, а при отсутствии действительных корней - значения 1; 3; -4;
сопоставляют результат, полученный в результате работы компьютерной программы, с экспериментальными фактами, теоретическими воззрениями и другой считающейся достоверной информацией об изучаемом объекте.
После проведения тех или иных правомерных сравнений может возникнуть необходимость уточнения метода или модели, составления нового алгоритма и соответствующей ему программы и повторения процедуры компьютерных расчетов, причем до тех пор, пока анализ получаемых результатов не подтвердит их приемлемость.
Понятие алгоритма. Исполнители алгоритмов. Свойства алгоритмов. Типы алгоритмов и формы их представления
Понятие алгоритма используется давно. Сам термин "алгоритм" произошел при переводе на европейские языки имени арабского математика IX в. Аль-Хорезми, которым были описаны правила (алгоритмы) выполнения основных арифметических действий в десятичной системе счисления.
В зависимости от характера занятий в своей повседневной жизни люди встречаются с различными практическими задачами: приготовление супа, проезд в общественном транспорте, решение квадратного уравнения, поиск слова в словаре и т.д. При решении любой подобной задачи человек обращается к продуманным заранее со всеми возможными вариантами предписаниям (инструкциям) о том, какие действия и в какой последовательности должны быть выполнены. В подавляющем большинстве случаев успех любой деятельности человека зависит от степени продуманности действий и их последовательности, возможных вариантов. Именно с целью успешного решения какого-либо определенного класса задач люди вырабатывают системы таких предписаний для использования разными людьми.
Алгоритм – это организованная последовательность конечного числа точных и понятных действий (команд, директив), необходимых для решения задачи опредленного типа.
Согласно этому определению рецепты изготовления какого-то определенного лекарства или печенья являются алгоритмами. И правило безопасного перехода пешеходом проезжей части улицы, содержащее указание человеку о его действиях, - тоже алгоритм. По своему назначению алгоритмы могуть быть как "бытовыми", так и вычислительными (алгоритм выполнения арифметического действия "столбиком", алгоритм Евклида – нахождения наибольшего общего делителя двух целых чисел).
Исполнители алгоритмов. Задача составления алгоритма не имеет смысла, если не известны или не учитываются возможности его исполнителя, ведь выполнимость алгоритма зависит от того, какие действия может совершить исполнитель (или как говорят, входят в его репертуар). Например, прочесть алгоритм решения системы линейных уравнений графическим методом сможет и первоклассник, а выполнить его, конечно же, нет. С другой стороны, малыш четырех-пяти лет не сможет прочесть правила (алгоритм) поведения за столом во время еды, но выполнить их сможет, если ему о них рассказать и показать, что они означают.
Но исполнителем алгоритмов может быть не человек, а автомат. Например, исправный автомат по продаже газированной воды работает согласно разработанному специально для него алгоритму. Алгоритмом описывается работа любого механического устройства.
В ряду всевозможных автоматов компьютер является лишь частным (хотя и наиболее впечатляющим) примером исполнителя, чье поведение реализуется на основе алгоритма. Более того, создание компьютеров оказало воздействие на развитие теории алгоритмов - одной из областей математики.
От компьютера, как от любого другого исполнителя, требуется четкое выполнение команд алгоритма. А от нас, как от разработчиков алгоритмов работы компьютера, требуется знание и соблюдение правил их составления. Эти правила заключаются в том, что алгоритм, предназначенный для исполнения автоматом, должен обладать пятью свойствами (удовлетворять пяти требованиям). Эти требования нашли отражение и в приведенном выше определении алгоритма. Требования к алгоритму объясняются тем, что такой исполнитель не имеет своего интеллекта, его возможности всегда ограничены.
