Числовые характеристики статистического распределения
Лабораторная работа № 1
Основы статистической обработки информации с использованием EXCEL. Определение некоторых числовых характеристик экспериментальных статистических данных.
Основной целью статистического анализа является выяснение некоторых свойств изучаемой генеральной совокупности. Если генеральная совокупность конечна, то наилучшая процедура — рассмотрение каждого ее элемента. Однако в большинстве задач используются либо бесконечные генеральные совокупности, либо конечные, но трудно обозримые. В этой ситуации необходимо отобрать из генеральной совокупности подмножество из n элементов, называемое выборкой объема n, исследовать его свойства, а затем обобщить эти результаты на всю генеральную совокупность. Это обобщение называется статистическим выводом.
Генеральная совокупность (популяция) W — полный набор объектов w, с которыми связана данная проблема. Эти объекты могут быть людьми, животными, изделиями и так далее. С каждым объектом связана величина (или величины), называемая исследуемым признаком (xi).
Различные значения признака, наблюдающиеся у членов генеральной совокупности (или выборки), называются вариантами, а числа, показывающие сколько раз встречается каждый вариант — их частотами.
В данном определении предполагается дискретное изменения признака. Однако, если мы измеряем непрерывную величину, то точность измерения и количество измерений в единицу времени тоже дадут некий дискретный набор.
Мы предполагаем, что измеряемый или исследуемый признак изменяется некоторым случайным образом. Произведя серию измерений, получим набор данных, которые, скорее всего, будут случайной выборкой из генеральной совокупности. Чтобы провести первичную обработку этой выборки, необходимо построить экспериментальное распределение данных по частотам или (если данные имеют явно непрерывный характер) по интервалам частот.
Числовые характеристики статистического распределения
В качестве характеристик измеримого признака вместо исходных значений величин или таблиц их частот используют числовые характеристики, называемые также статистическими мерами.
· Среднее арифметическое 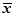 : Определяется по формуле
: Определяется по формуле
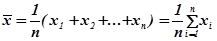 , где xi — значения вариант.
, где xi — значения вариант.
· Медиана 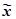 — срединное значение для ряда измерений n. Для ее вычисления необходимо все наблюдения расположить в порядке возрастания или убывания результатов. Если n — нечетное число, то медиана просто является числом, находящимся в середине упорядоченной последовательности. При четном n
— срединное значение для ряда измерений n. Для ее вычисления необходимо все наблюдения расположить в порядке возрастания или убывания результатов. Если n — нечетное число, то медиана просто является числом, находящимся в середине упорядоченной последовательности. При четном n 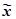 равна среднему арифметическому двух расположенных в середине значений упорядоченной последовательности.
равна среднему арифметическому двух расположенных в середине значений упорядоченной последовательности.
· Мода — (наиболее вероятное значение) является наиболее часто встречающейся в выборке величиной.
· Размах вариации R — разность между максимальным и минимальным значениями признака в ряде измерений.
R = xmax -xmin
· Среднее линейное отклонение d — среднее арифметическое абсолютных величин отклонений вариантов от их средней арифметической.
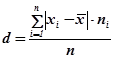 , ni — частота признака xi.
, ni — частота признака xi.
· Дисперсия D — среднее арифметическое квадратов отклонений вариантов от их средней:
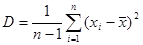
· Среднее квадратичное отклонение s — квадратный корень из дисперсии.
Под формой статистического распределения понимается форма его графика — полигона или гистограммы. Различают симметричные формы и несимметричные (асимметричные).
Распределение называется симметричным, если веса любых вариантов, равноотстоящих от среднего, равны между собой.
На практике такого совпадения для всех вариантов обычно нет и симметричными считаются распределения, в которых веса вариантов, равноотстоящих от среднего, отличаются незначительно. (Пример 1 — близок к симметричному распределению).
Асимметричные распределения можно разбить на три вида:
· умеренно асимметричные — распределения, у которых частоты, находящиеся по одну сторону от наибольшей, больше (или меньше) частот, находящихся по другую сторону от наибольшей на таком же “расстоянии”.
· крайне асимметричные — распределения, у которых частоты или все время возрастают, или все время убывают.
· U-образные — частоты сначала убывают, а затем возрастают.
В табл. № 1 представлены экспериментальные данные, полученные после медицинского обследования 100 студентов МаГУ. Необходимо оценить числовые характеристики выборки студентов, проанализировать форму распределения частот.
Таблица 1
