Анализ связи номинальных признаков

Корреляция качественных признаков

Анализ содержания исторических источников нередко приводит к необходимости обработки качественной информации. Такая ситуация является типичной при изучении различных анкет, материалов переписей, личных карточек рабочих и т. д., а также при анализе нарративных источников. Формализация данных, содержащихся в источниках такого типа, характеризуется тем, что свойства (признаки) изучаемых объектов или явлений могут быть описаны лишь на качественном уровне, т.е. измерение этих признаков с помощью количественных шкал не представляется возможным.

Общая классификация типов признаков нами ранее. Рассмотрим подробнее типы качественныхпризнаков, которые разделяются на качественные признаки рангового (порядкового) и номинального (классификационного) типа (см. рис. 18).

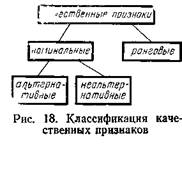Измерение по номинальной(простейшей из шкал) эквивалентно отнесению объекта к одному из классов по данному признаку. Частным случаем номинальной является шкала измерения альтернативных(дихотомических) признаков, т.е. шкала, включающая два класса (градации), соответствующих, например, наличию и отсутствию у объекта того или иного качества.

Порядковыешкалы — это более высокий уровень измерения качественных признаков. Градации рангового признака, измеренного в такой шкале, упорядочены по степени проявления соответствующего свойства. Ранговый признак задает не простую группировку объектов, как номинальный, а такую, при которой группы являются упорядоченными.

Рассмотрим несколько примеров качественных признаков различных типов. Номинальные признаки: наименование продукции, тип хозяйства, профессия, национальность, пол (последний признак является альтернативным). Ранговые признаки: сословие, образование, квалификация.

Основное внимание мы будем уделять важной проблеме измерения связи качественных признаков. Наиболее разработанными являются методы анализа взаимосвязи качественных признаков с одинаковыми уровнями измерения.

Анализ связи номинальных признаков

Традиционные меры связи.Традиционный подход к построению мер связи нормальных признаков основан на проверке предположения о статистической независимости рассматриваемых признаков.

Рассмотрим вначале вопрос о взаимосвязи двух альтернативныхпризнаков, таблица сопряженности которых имеет следующий вид¹ (см._табл. 1).

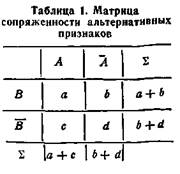Здесь буквами А и А обозначены наименования двух классов по первому признаку, а В и В — по второму. Числа в клетках табл. 1 определяют численности объектов, обладающих сочетанием соответствующих свойств. Так, с равно числу объектов, обладающих свойством А и не обладающих свойством В.

Пример 1.По выборочным данным, относящимся к концу XIX в., изучим зависимость между размером имения и типом хозяйства.

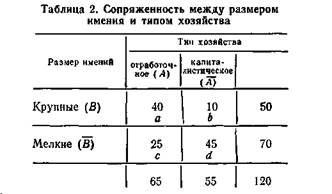
Как следует из табл 2, число, например, крупных хозяйств отработочною типа равно 40, общее число крупных хозяйств (а + b) равно 50, а общее число хозяйств отработочного типа (а + с) — 65

Условие статистической независимости признаков в данном случае эквивалентно требованию, чтобы, например, доля крупных хозяйств среди имений отработочного типа была равна доле крупных хозяйств во всей изучаемой совокупности, т.е. чтобы

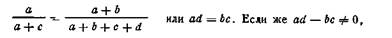
то рассматриваемые признаки являются взаимосвязанными Данные табл 2 показывают, что ad = 40х45, bс=10х25, т е ad—bc>0, что указывает на наличие связи типа хозяйства с размером имения.

Для оценки степени связи альтернативных признаков используют обычно следующие два коэффициента

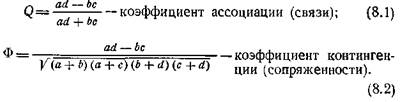
Оба коэффициента Q и Ф принимают значения от —1 до + 1 и равны 0, если признаки статистически независимы

Коэффициент Q равен +1 в случае полной связанности, т.е. либо все объекты со свойством А обладают одновременно и свойством В (с = 0), либо все объекты со свойством В обладают одновременно и свойством А (b = 0) Значение -1 коэффициент Q принимает в случае полной отрицательной связанности (а = 0 или d = 0)

Коэффициент Ф равен +1, если все объекты со свойством А обладают и свойством В, а все объекты со свойством В обладают и свойством А (b = 0, с = 0). Значение -1 коэффициент Ф принимает в случае, когда все объекты со свойством А не обладают свойством В, а все объекты со свойством В не обладают свойством А (а =0 и d=0).

Таким образом, числовые значения коэффициентов Q и Ф для одних и тех же данных могут существенно отличаться друг от друга, поскольку эти коэффициенты измеряют различные аспекты взаимосвязи в 4-клеточной таблице. Ф предназначен для измерения степени двусторонней взаимосвязи между рассматриваемыми альтернативными признаками, в то время как Q отражает лишь односторонне направленную связь Значения этих коэффициентов совпадают лишь при наличии полной двусторонней взаимосвязи Q³Ф. Так, определение величины коэффициентов Q и Ф для данных табл 2 приводит к следующим результатам

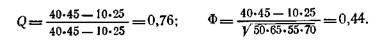
Оба коэффициента Q и Ф в данном примере принимают положительные значения, т.е. связь между рассматриваемыми признаками прямая (наличие свойства А связано, как правило, с наличием свойства В).

Довольно высокое значение коэффициента связи Q (0,76) определяется тем, что абсолютное большинство крупных хозяйств (40 из 50, т.е. 80%) относится к отработочному типу. Величина коэффициента сопряженности Ф (0,44) значительно уступает величине Q. Это связано с тем, что связь данных признаков носит преимущественно односторонний характер (среди крупных хозяйств отработочные составляют 80%, в то время как среди хозяйств отработочного типа около 40% (25 из 65) составляют мелкие хозяйства).

Теоретико-информационные меры связи.Развитие математико- статистических методов в последние десятилетия привело к появлению нового подхода к проблеме оценки связи качественных признаков. В основе этого подхода лежит представление о том, что мера связи признаков должна не столько оценивать степень их статистической независимости, сколько характеризовать возможность прогноза значений одного из признаков по значениям другого.

Самый точный прогноз достигается в ситуации, когда для каждого из значений одного признака можно однозначно указать соответствующее значение второго. Мера связи в этой ситуации, соответствующей «полной связи» между признаками, должна принимать максимальное значение, равное 1. Критерием отсутствия связи в рамках данного подхода обычно также считается статистическая независимость признаков; в этом случае мера связи должна принимать минимальное, нулевое, значение.

Таким образом, современная трактовка понятия «полная связь» между признаками X и У означает, что знание значения признака X устраняет всякую неопределенностьв знании значения признака Y. Для уменьшения неопределенности необходимо получить некоторое количество информации.Измерение статистической связи признаков сводится здесь к оценке относительно уменьшения неопределенности Y при получении знания об Х.

Пример 3.Поясним сказанное на примере данных тлбл 4, содержащей 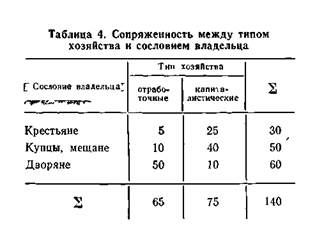иллюстративные сведения о сопряженности признаков «сословие» (X) и «тип хозяйства» (У) Знание значения признака X в данном примере существенно снижает неопределенность в знании значений признака Y. Так, если X принимает значение х₃ («дворяне»), то Y почти наверняка (с вероятностью 0,93 = 50/60) принимает значение у₁ («отработочный тип»). Если Х = х₂ («крестьяне»), то неопределенность в знании Y также существенно снижается с вероятностью 0,80 = = 40/50 Y = y₂ («капиталистический тип») и т.д. Отметим, что неопределенность в знании значений признака Y, взятого отдельно, высока— вероятности значений у₁ и у₂ равны 0,46 = 65/140 и 0,54 = 75/140 соответственно.

Количественный анализ неопределенности и информации осуществляется на основе результатов теории информации,начало которой было положено в конце 1940-х годов. Основным, фундаментальным понятием теории информации является энтропия — мера неопределенности. Применительно к нашей задаче анализа качественных признаков энтропия можег быть определена следующим образом.

Пусть изучаемое явление (признак х) характеризуется mсостояниями (классами) х₁, х₂, ..., х_т и имеет статистическую природу. Обозначим через p_i вероятность того, что признак X принимает i-e значение х_i (при этом p₁+p₂+…+ p_m=l). Тогда энтропия, т.е. мера неопределенности признака х вычисляется по формуле

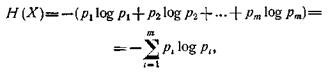
где log p_i,— логарифм при основании 2 от величины р_i.

При анализе эмпирических данных роль вероятностей р_i играют их выборочные оценки (частости, доли) n_i/N где N — общее число объектов в выборке; n_i — число объектов i-ro класса x_i.

Нетрудно показать, что энтропия H действительно соответствует интуитивным представлениям о степени неопределенности. Минимальное значение энтропии равно нулю, и достигается оно при условии, что все вероятности равны нулю, кроме одной (например, p_i), которая равна 1. Содержательно это означает, что все объекты принадлежат одному классу (x_i), т.е. какая-либо неопределенность в знании значений признака X отсутствует. Максимальное значение энтропии равно log m, и достигается оно при таком распределении вероятностей, когда все они одинаковы и равны p_t=1/m(1£ i£ m). Это свойство энтропии как меры неопределенности также согласуется с представлением о том, что максимальная неопределенность, разнообразие изучаемой системы соответствуют равновероятному распределению объектов по классам х_i, ..., х_т.

Поскольку максимальное значение энтропии (logm) зависит от числа классов т, то на практике часто используют нормированную энтропию H*=H/logm, которая принимает значения в интервале [0, 1]. Зависимость величины H* от распределения вероятностей иллюстрируется графически на рис. 19 (m = 4; число над каждым столбиком обозначает величину соответствующей вероятности р_i).

Вычисление энтропии Н* для признаков X и Y из табл.4 приводит к следующим результатам. Для признака X («сословие») частоты трех классов равны соответственно 30/140, 50/140 и 60/140, а для признака Y («тип хозяйства») — 65/140, 75/140. Отсюда получаем:

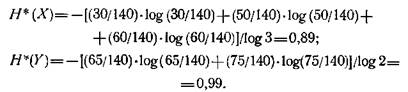
Таким образом, мера неопределенности обоих признаков оказывается (по данным табл. 4) весьма высокой.

Отметим, что чувствительность величины энтропии к отклонениям от равномерного распределения частот послужила причиной активного использования энтропийного анализа в исторических исследованиях для оценки степени социально-экономического неравенства, имущественной дифференциации.

Перейдем теперь к определению понятия «количество информации», особенно важного для построения мер связи качественных признаков. Пусть знание значений признака Х уменьшает неопределенность в знании значений признака Y. Оставшуюся меру неопределенности обозначают Н_х(Y) и называют условной энтропией. Количество информации I(XY) определяется как уменьшение неопределенности признака X за счет информации, полученной о связи X и Y:

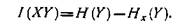
В теории информации показано, что количество информации I(XY) может быть вычислено по формуле

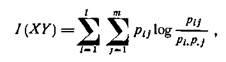8.11

где p_ij — вероятность того, что признак X характеризуется i-м классом, а признак Y — j-м классом; p_i. — вероятность i-ro значения признака X; р_.j — вероятность j-го значения признака Y.

Формула (8.11) для количества информации симметрична относительно X и Y, т.е. I(XY)=I(YX), поэтому I(XY) называют также взаимной информацией X и У.

Взаимная информация обращается в нуль тогда и толь ко тогда, когда признаки X и У статистически независимы. Максимальное значение взаимной информации, равное H(X) или H(Y), соответствует функциональной зависимости (полной связи) признаков X и Y, когда каждому значению x_i признака X соответствует единственное значение у_i признака Y.

При анализе взаимосвязи признаков на основе взаимной информации I(ХY), когда таблица сопряженности строится на основе выборочных данных, возникает задача о значимости статистической зависимости, если I(XY)¹0. Исходя из доказанных в теории информации свойств I(XY), в данном случае пользуются той же методикой, что и изложенная выше для определения уровня значимости коэффициента X² с помощью критерия X². По таблице X² для заданных уровней значимости (например, а = 0,01), числа степеней свободы k=(l — 1) (т — 1) и объема выборки (N) определяется критическое значение I_Kp = X²/2N, которое далее сравнивается с фактическим I_ф(XY). Если I_кр³I_ф(XY), то с заданной степенью уверенности принимается гипотеза о независимости X и Y, если же I_ф(XY)³I_кр, то утверждается, что на данном уровне значимости гипотеза о независимости X и Y неверна.

Пример 4.Обратимся вновь к данным табл. 4. Как уже было определено выше, при уровне значимости а = 0,01 и числе степеней свободы k = 2 критическое значение Х²_кр = 9,21. Следовательно, в данном случае I_кр=X²/2N=9,21/(2 • 140) =0,033 Вычисление по формуле (8.11) взаимной информации для признаков X и Y по данным табл. 4 приводит к величине I_ф(XY)=0,321. Имеем I_ф(XY)³I_кр, следовательно, гипотеза о независимости X и Y на данном уровне значимости а = 0,01 неверна (нет и одного шанса из ста, что признаки X и Y независимы).

Установив факт существенности связи признаков, далее следует измерить ее силу. Наибольшее распространение получила мера связи, для построения которой необходимо пронормировать взаимную информацию I(XY) на H(XY):

Однако использование этих коэффициентов для разделения признаков на «зависимые» и «определяющие» не имеет достаточного обоснования.