Характеристики сигнала и шума на выходе детектора

Постановка задачи

Функциональная схема анализируемого устройства:

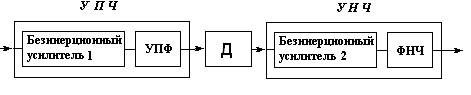
Она содержит последовательно соединенные первый безинерционный усилитель, узкополосный фильтр, нелинейную цепь, в данном случае фазовый детектор, второй безинерционный усилитель и фильтр низкой частоты. Совокупность первого безинерционного усилителя и узкополосного фильтра представляет собой резонансный усилитель промежуточной частоты (УПЧ), который предназначен для усиления и выделения полезного сигнала из шумов. Выделение информационного сообщения, заложенного в частоту сигнала, выделяется с помощью нелинейной цепи т.е. детектора. Второй усилитель это УНЧ, предназначен для усиления и выделения полезного сигнала из шумов.

На вход анализируемого устройства воздействует аддитивная смесь шума с энергетическим спектром W0 и сигнала 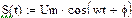т.е. .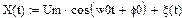

Задача сводится к оценке помехоустойчивости.

Характеристики сигнала и шума на выходе УПЧ

На вход УПЧ воздействуют две составляющих: шум и сигнал, так как УПЧ это линейная цепь, то допустимо отдельно рассматривать сигнал и шум, а затем сложив их, получается итоговый сигнал на выходе.

Квадрат АЧХ УПЧ представленный аналитически и графически:

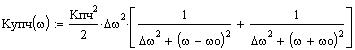
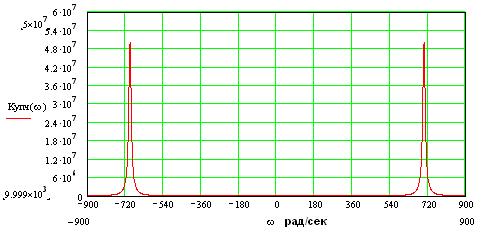
Сигнал

Сигнал, проходя через УПЧ просто усиливается, а его спектральная характеристика остается неизменной, т. е. энергетический спектр сигнала на выходе будет иметь вид:

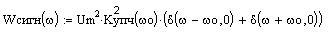
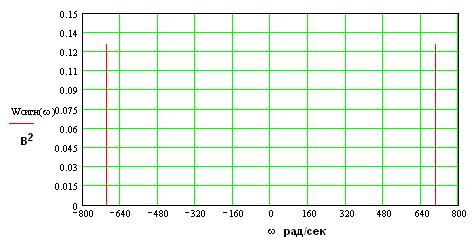
Шум

На вход УПЧ воздействовал белый шум, равномерный во всей полосе частот, имеющий дельта-видную корреляционную функцию, но проходя через частотно-избирательную цепь его спектр мощности изменится так, что максимум будет на резонансной частоте.

Аналитически спектр мощности шума на выходе УПЧ будет описываться выражением:

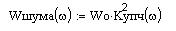
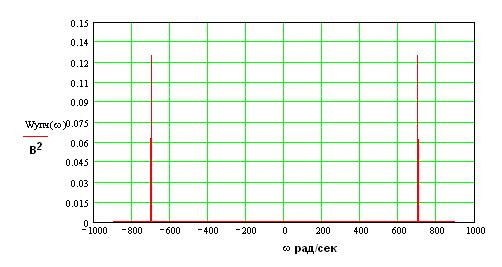
Спектральное представление:

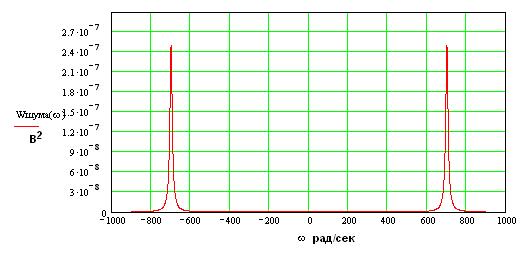
Таким образом, видно, что сужение полосы пропускания ведет к снижению мощности шума на выходе УПЧ т. е. на входе детектора, что улучшает соотношение сигнал/шум и общую помехоустойчивость.

Для нахождения корреляционной функции применим преобразование Винер-Хинчина:

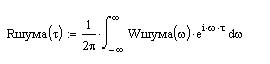
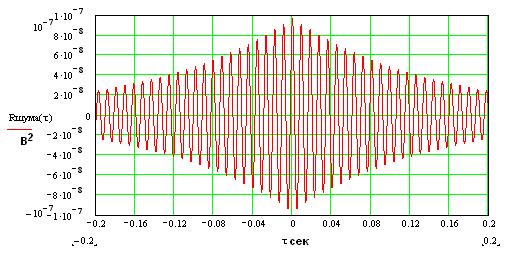
нормированная КФ:

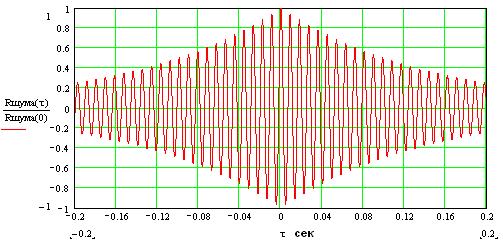
Огибающая для ненормированной корреляционной функции шума будет иметь вид:

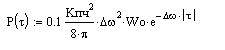
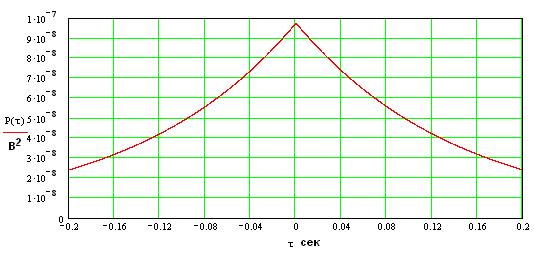
Сигнал и шум

Так как цепь линейная, то для нее справедлив принцип суперпозиций, т. е. итоговый энергетический спектр сигнала и шума проще всего найти как сумму их отдельных составляющих, то есть:

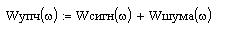
Для нахождения отношения сигнал шум необходимо найти амплитуду несущей на выходе УПЧ и дисперсию шума. Дисперсия шума это значение корреляционной функции от нуля, амплитуда несущей находится как произведение коэффициента усиления УПЧ и амплитудного значения входного напряжения.

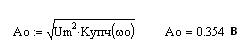
Сигнал/шум на выходе УПЧ:

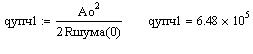
Характеристики сигнала и шума на выходе детектора

Как известно, в фазовом детекторе выходной сигнал пропорционален фазе сигнала на входе с коэффициентом крутизны детектирования. Фаза входного сигнала определяется как:

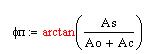
где Ac, As – косинусоидальная и синусоидальная квадратурные компоненты, Ao – амплитуда несущей.

так как Ao >> Ac в знаменателе последним можно принебречь:

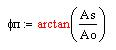
так как аргумент арктангенса стремится к нулю то приближенно справедливо следущее:

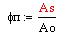
Таким образом, помеха вносит дополнительную шумовую составляющую в полезный сигнал с эквивалентной амплитудой:

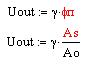
Из этого выражения видно, что для фазового детектора, чем выше отношение несущая/шум на входе, тем меньше шума получается на выходе.

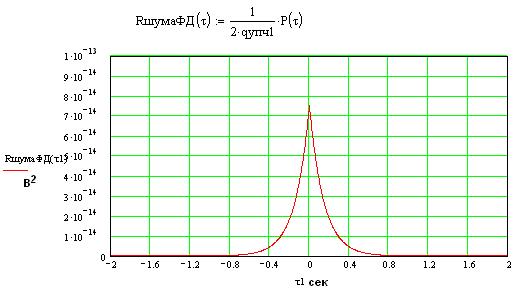
Огибающая корреляционной функции шума на выходе детектора:

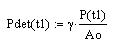
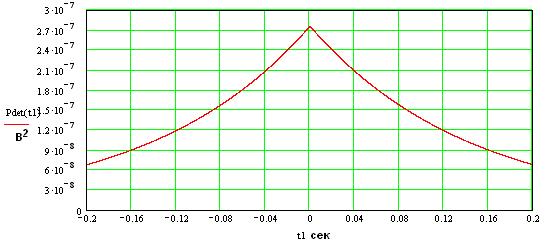
Сигнал на выходе фазового детектора:

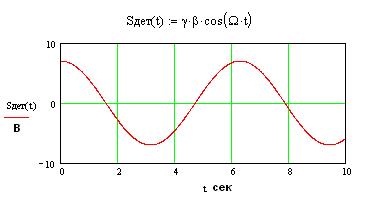
Сигнал/шум на выходе детектора:

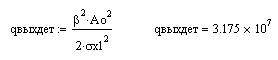
СКО и дисперсия шума на выходе детектора:

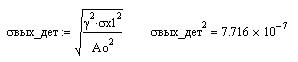
Энергетический спектр шума на выходе детектора:

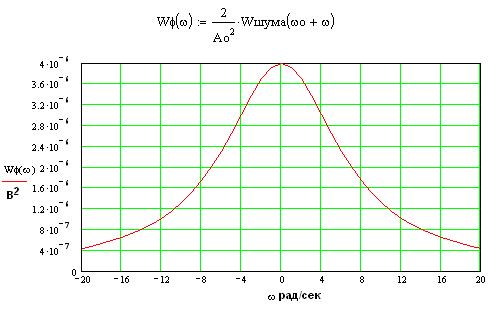
Корреляционная функция шума на выходе детектора: