Метод Циклического покоординатного спуска

В данном методе на каждой итерации выполняется n(количество координат) одномерных минимизаций (спусков) вдоль единичных орт. Этот метод работает особенно хорошо, если линии равного уровня расположены вдоль координатный осей.

Начальный этап

Выбрать x1, e, k=1, l=1.

Основной этап

Шаг 1

(1) В качестве направления p выбрать 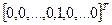, где ненулевая позиция имеет индекс l.

(2) Найти L как результат минимизации функции по направлению p.

(3)

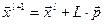
(4) Если l<n то Шаг 2, иначе повторить Шаг 1 с l = l+1.

Шаг 2

(1) Вычислить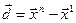

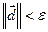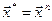(2) Проверить КОП: если , то , иначе 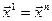, l=1 и на Шаг 1.

Метод параллельных касательных

Начальный этап:

Выбрать х1, ε = 10^-4 – 10^-8 установить k = 1;

Основной этап:

Шаг 1.

Из точки x¹ выполнить антиградиентный в точку x²= x¹+α₁р¹, где p¹=-Ñу¹.

Шаг 2.

Последовательно выполнить две операции:

1. Антиградиентный спуск в точку x³.

2. Вычислить ускоряющее направление d=x³-x¹ и, не останавливаясь совершить ускоряющий шаг в точку x⁴=x³+α₃d.

Шаг 3.

Проверить КОП: 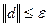- остановиться x*=x⁴.

Иначе:

1. Обозначить x² как новую начальную x¹=x², а точку x⁴ как новую точку ускорения x²=x⁴.

Перейти к шагу 2.

Метод Гаусса-Зейделя

Начальный этап

Выбрать х1, ε = 10^-4 – 10^-8 установить k = 1;

Основной этап:

Шаг 1.

Выполнить серию одномерных поисков вдоль координатных орт

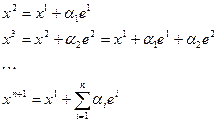
Шаг 2.

Вычислить ускоряющее направление и проверить КОП: 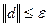, если выполняется, минимум найден: x*=xⁿ⁺¹.

Иначе:

1. Выполнить ускоряющий шаг в новую точку хⁿ⁺²

2. Обозначить последнюю точку как начальную и вернуться на шаг 1.

Метод комплексов Бокса

Комплекс-метод предназначен для отыскания условного экстремума непрерывной целевой функции (1) в выпуклой допустимой области.

При использовании метода принимаются следующие предпо­ложения:

1. Задача поиска экстремума функционала (1) решается при наличии ограничений 1-го и 2-го рода.

2. Значения целевой функции и функций ограничений могут быть вычислены в любой точке допустимой области изменения независимых переменных.

3. Допустимая область выпукла.

4. Значения целевой функции и функций ограничений вычисляются без ошибок.

Идея комплекс метода заключается в последовательной замене точек некоторой конфигурации, удаленных от экстремума, на более близкие к нему.

В отличие от симплексного метода, в комплексе-методе используется случайный набор N точек – Комплекс, а число точек Комплекса определяется по правилу:

(5)

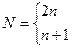
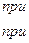
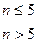
где n – число независимых переменных.

Вычислительная последовательность (алгоритм) комплекс-метода включает в себя следующие этапы.

1) Формируется исходный комплекс. Координаты вершин исходного Комплекса хij вычисляются последовательно с помощью равномерно распределенных на интервале (0;1) псевдослучайных чисел rij:

(6)

xij=gi+rij(hi - gi), i=1, 2,…,n, j=1, 2, ,N.

В каждой вершине с номером j проверяется выполнение ограничений 2-го рода (ограничения 1-го рода выполняются автоматически).

Точка фиксируется как вершина Комплекса, если в ней удовлетворяются все ограничения. Если же ни в одной из точек ограничения не выполнены, то формуле (6) вычисляются координаты новых точек, в которых вновь проверяется ограничения.

Пусть число точек, удовлетворяющих ограничениям 2-го рода Р (Р≥1), тогда (N–P) – число точек, в которых ограничения нарушены.

Далее для каждой из еще незафиксированных вершин выполняется операция по ее смещению к центру Р вершин Комплекса, при этом новые координаты точки х*ij вычисляются по формуле

(7)

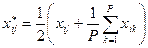, i=1, 2,…, n, j=P+1, P+2,…,N.

Процесс смещения j-й точки продолжается до тех пор, пока для нее не будут выполнены все ограничения. Такой момент обязательно наступит, поскольку допустимая область выпукла. Точка фиксируется как новая вершина Комплекса (Р увеличивается на единицу), после чего операция смещения повторяется для очередной вершины.

(8)

2) Для всех N вершин Комплекса вычисляются значения целевой функции Fi:

Fj=F(xj), 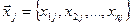, j=1, 2,…,N.

(9)

3) Выбираются наилучшее R и наихудшее S (с точки зрения экстремума) значения из массива Fi:

R=FG; S=FD.

где G – номер самой «хорошей»; а D – самой «плохой» вершины.

4) Определяются координаты Ci центра Комплекса с отброшенной «наихудшей» вершиной:

(10)

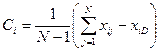, i=1, 2,…,n.

5) Проверяется условие окончания поиска. Для этого вычисляется величина В:

(11)

.

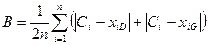Если В<ε (ε – заданная точность вычисления), т.е. среднее расстояние от центра Комплекса до худшей (D) и лучшей (G) вершин меньше ε, то поиск заканчивают, считая экстремум найденным.

В противном случае вычисления продолжаются:

(12)

6) взамен наихудшей вычисляются координаты новой точки Комплекса:

xi0=2,3Ci – 1,3xiD, i=1, 2,…,n.

В этой новой точке проверяется выполнение ограничений 1-го рода. В случае, если ограничения нарушаются, xi0 принимает значения gi+ε или hi–ε в зависимости от того, в какую сторону i-е ограничение нарушено;

(13)

7) для новой точки проверяется выполнение ограничение 2-го рода. Если хотя бы одно из ограничений нарушено, то новую точку смещают к центру Комплекса на половину расстояния:

.

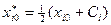Процесс смещения продолжают до тех пор, пока все ограничения 2-го рода не будут соблюдены.

8) В новой точке вычисляют значения целевой функции F0:

(14)

.

(15)

9) Если F0 оказывается хуже S (значение целевой функции в наихудшей точке D предыдущего комплекса), т.е. новая точка находится дальше от экстремума, чем вершина с номером D, то новая вершина находится смещением xi0 на половину расстояния к лучшей из вершин комплекса G:

.

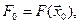
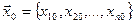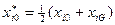Затем вновь вычисляют значение целевой функции F0 и сравнивают его с S. Смещением к лучшей вершине по формуле (15) продолжают до тех пор, пока F0 не станет лучше S.

За счет этой процедуры происходит последовательное сжатие комплекса к лучшей вершине.

10) Если вычисленное в новой точке х0 значение F0 лучше S, то в Комплексе на месте наихудшей точки хD фиксируется точка х0 и значение S заменяется на F0.

Затем вычисления повторяются, начиная с п. 3, и продолжаются до тех пор пока не будет выполнено условие остановки, т.е. не будет найден с заданной точностью экстремум целевой функции.

Метод Хука-Дживса (конфигураций)

Эффективность прямого поиска точки минимума можно повысить, если на ка­ждом k-м шаге поиска соответствующим образом выбирать направление спуска. Для этого на каждом k-м шаге выделяют предварительный этап исследующего поиска. Целью этого этапа является выбор направления спуска путем исследования поведения целевой функции f(x) в окрестности точки xk-1, найденной на предыдущем шаге. В результате выполнения этапа исследующего поиска находится точка xk, для которой f(x^k) < f(x^k-1). Направление спуска, завершающего k-w. шаг поиска, определяется вектором x^k - x^k-1. Такая стратегия поиска, получила название метода Хука - Дживса.

Исследующий поиск 1

Вдоль координатных орт выполняют малые шаги. Т.е. локальное обследование точки х¹, для поиска лучшей чем х¹ точки. Если шаг удачный то точку фиксируют и продолжают шаги из неё, если не удачный то делают шаг в противоположную сторону, если полученная точка снова хуже, то по этой оси шаг не делается.

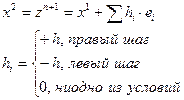
Ускоряющий поиск

Выполняем единичный шаг вдоль направления 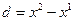, 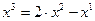. Затем производим исследующий поиск в окрестности x³, в надежде найти точку лучшую чем x².

Начальный этап

β = 10, ε = 10-4 – 10-8 , k = 1, х¹, h₁= … =h_n=0.1;

Основной этап

Шаг 1.

Выполнить ИП1 и отыскать т. х² для которой .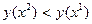

Шаг 2.

Если ИП1 удачен т.е. найдена х², то перейти на шаг 3, иначе, но в то же время h<ε необходимо уменьшить шаг в β раз и вернуться на шаг 1. При h<ε остановиться х* = х¹.

Шаг 3.

Выполнить УП в пробную точку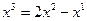

Обозначить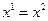

В окрестности х3 попытаться ИП2 найти т. х⁴ «лучшую» чем х¹.

Шаг 4.

Если ИП2 удачен, то положить 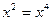и вернуться на шаг 1.

Иначе: уменьшить шаг в β раз и вернуться на шаг 1.

Метод Хука-Дживса с одномерной минимизацией

Данный метод является аналогом метода циклического покооординатного спуска (ЦПС) с ускоряющим шагом. Начиная со второй итерации, устанавливается новый способ построения направления ускоряющего поиска. Организацию итерационной процедуры и отличие метода Хука-Дживса с одномерной минимизацией от метода ЦПС раскрывает представленное ниже пошаговое описание алгоритма.

Начальный этап

(1) Исходные данные - базовая точка x, погрешность вычисления минимума e, матрица координатных направлений p = {pⁱ}, i = 1,2,...,n, где pⁱ = eⁱ - i-ый единичный орт в Rⁿ, т.е. eⁱ = 1 и e_jⁱ = 0 при всех i ¹ j.

(2) Начальную точку x¹ принять равной базовой точке: x¹ = x.

Основнй этап

Шаг 1.

Выполнить ЦПС из начальной точки x¹ в конечную точку xⁿ⁺¹, последовательно решая n-задач одномерной минимизации вдоль координатных направлений p.

Шаг 2.

Проверить критерий окончания поиска:

(1) построить направление ускоряющего поиска d = xⁿ⁺¹ - x;

(2) если ½½d½½ << e, остановиться.

Шаг 3.

Определить начальные условия для очередной итерации:

(1) найти оптимальный шаг a_n+1 в точку xⁿ⁺² = xⁿ⁺¹ + a_n+1d;

(2) взять точку xⁿ⁺² за новую начальную точку x¹ = xⁿ⁺², а точку xⁿ⁺¹ за новую базовую x = xⁿ⁺¹;

(3) вернуться на шаг 1.

Метод Ньютона

Если f(x) является дважды дифференци­руемой в Rⁿ, то эффективность процесса поиска точки х* ее минимума можно повысить, используя информацию не толь­ко о градиенте этой функции, но и о ее матрице Гecce H(x). Алгоритмы такого поиска обычно относят к ме­тоду Ньютона. В простейшем варианте алгоритма на каждой k-й итерации целевая функция аппроксимируется в окрестно­сти точки x_k-1 (на первой итерации в окрестности начальной точки х0) квадратичной функцией 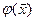и затем определяется точка x_k минимума функции 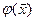. На следующей, (k+1)-й итерации строится новая квадратичная аппроксимация уже в окрестности точки x_k.

Начальный этап:

Выбрать x₀, e, k=1.

Основной этап

Шаг 1

(1) Строится Ньютоновское направление: 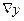- градиент в заданной точке, H – матрица Гессе

(2) Найти 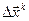как результат решения системы уравнений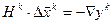

(3)

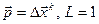
(4)

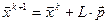
Шаг 3

Проверить КОП: если 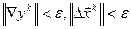, то 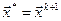, иначе на Шаг 1.

Метод Зангвилла

Начальный этап

Выбрать константу остановки e > 0 и начальную точку x₁. Положить y₁ = x₁, k = j =1, 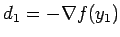и перейти к основному этапу.

Основной этап

Шаг 1. Взять в качестве 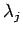оптимальное решение задачи минимизаци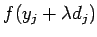и при 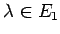и положить 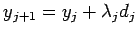. Если 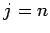, то перейти к шагу 4; в противном случае перейти к шагу 2.

Шаг 2. Положить 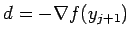и взять в качестве 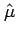оптимальное решение задачи минимизаци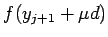и при 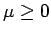. Положить 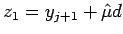, 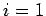и перейти к шагу 3.

Шаг 3. Если 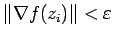, то остановиться; 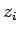-- оптимальное решение. В противном случае взять в качестве 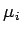оптимальное решение задачи минимизаци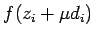и при 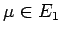. Положить 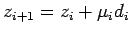. Если 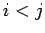, то заменить 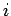на 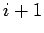и повторить шаг 3. В противном случае положить 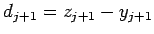, заменить 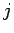на 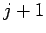и перейти к шагу 1.

Шаг 4. Положить 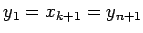, , 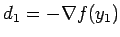заменить 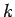на 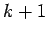, положить 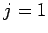и перейти к шагу 1.

Метод Флетчера-Ривса

Метод сопряжённых направлений основан на свойствах векторов сопряженных относительно некоторой квадратной матрицы. Различие в способах построения системы сопряженных векторов, определяющих сопряжённые направления спуска, порождает несколько алгоритмов этого метода. В качестве матрицы сопряжений берётся матрица Гессе. Особенность алгоритмов метода сопряженных направле­ний состоит в том, что систему сопряженных векторов строят последовательно в процессе выполнения итераций, причем найденный на очередной, k-й итерации вектор pk определяет на этой итерации направление спуска. Для не квадратичных функций получаемые направления, в конце концов, перестают быть взаимносопряженными поэтому, как и в ДФП через n шагов вектор направления делают равным антиградиенту.

Начальный этап

Выбрать x¹, e, k=1.

Основной этап

Шаг 1.

Построить вектор pk:

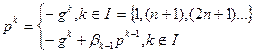
Шаг 2.

Найти новую точку 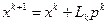как результат одномерного поиска полученного направления .

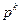Шаг 3.

Проверить КОП: .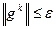

Расчетное соотношение Флетчера-Ривса

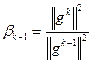
Метод Пауэлла

Метод достаточно прост в реализации и обладает квадратичной сходимостью вблизи минимума. Стратегия метода базируется на свойстве квадратичных функций параллельного подпространства: если x¹ минимум квадратичной функции по вектору p, а x² минимум этой же функции по вектору параллельному предыдущему, то .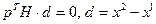

Первый варианталгоритма метода Пауэлла

Начальный этап

(1) Выбрать x1, e, k=1.

(2) Положить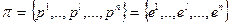

Основной этап:

Шаг 1.

(1) Выполнить n переходов по векторам базиса :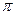

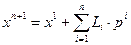
(2) Определить новое направление и спуститься вдоль него: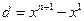

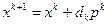
Шаг 2.

Проверить КОП: если 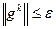,или k = n (для квадратичных функций) то прекратить поиск, иначе Шаг 3

Шаг 3.

Построить новую поисковую систему: из предыдущей системы удаляется первый вектор, а в конец добавляется вектор d.

Таким образом изменение системы поиска выглядит так:

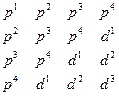
Второй вариант алгоритма метода Пауэлла

Отличается от первого варианта тем, что изначально строится поисковая система где первый и последний вектор параллельны:

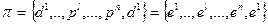
Изменение поисковой системы выглядит так: