Производственные функции. Однородные и линейные производственные функции. Производственная функция Кобба-Дугласа

ПФ– эк.-мат. уравнение, связывающее величины затрат с величиной производства продукции. Общий вид: y=f(x1,x2,..xn). В основе лежит теория предельной полезности и предельных издержек (каждая доп. единица однотипной продукции обладает меньшей полезностью и ведет к все большим издержкам).

Свойства ПФ:

1) с ростом ресурсов увеличивается объем производства ∂Y/∂Xi>0

2) c ростом ресурсов скорость выпуска снижается ∂²Y/α∂²Xi<0

Им удовлетворяет функция Кобба-Дугласа вида 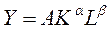, где Yt - объем производства продукции, Lt -численность занятых, Kt - объем основных фондов.

Производственная функция Кобба-Дугласа- зависимость объема производства (У) от создающих его труда (L) и капитала (K).

Свойства К-Д:

1. α, β – постоянные коэффициенты эластичности.

α– коэффициент эластичности объема производства по капиталу – на сколько изменится объем производства , еслиК увеличится на 1%, а численность занятых останется неизменной.

β– коэффициент эластичности объема производства по труду – на сколько изменится объем производства , если 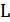увеличится на 1%, а К останется неизменной.

(имеют смысл, если в экономике использование факторов производства явл. эффективным)

2. В эффективной экономике выполняются следующие условия:

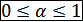и

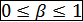
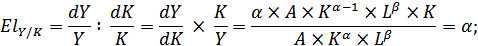
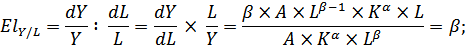
В реальности обычно E<1. Тогда вместо функции К-Д используют CES-функции (с E≠1).

3. Свойства эффекта от масштаба.

Эффект масштаба - Соотношение между относительным изменением объема выпуска и относительным изменением затрат факторов производства.

Свойства эффекта от масштаба, если:

1) 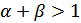- происходит увеличение эффекта от масштаба;

2) 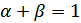- постоянный эффект от масштаба;

3) – отрицательный эффект от масштаба.

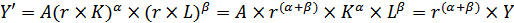
Таким образом, У связано с увеличением факторов через коэффициент .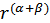

4. Логарифмирование К-Д приводит ее к линейному виду относительно α и β, что позволяет проводить их оценку с использованием методов линейного регрессионного анализа: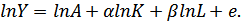

Характеристики ПФ: средняя производительность; трудоемкость; капиталоотдача и капиталоемкость; капиталовооруженность; предельная производительность труда (∂Y/∂L) и предельная капиталоотдача, эластичность по капиталу (∂Y/Y:∂K/K) и по труду; предельная норма замещения труда основными средствами (ψ_K/L=dK/dL); эластичность замещения труда ОФ:

.

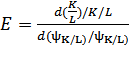Если функция К-Д имеет вид 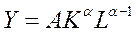, то влияние факторов можно разделить на экстенсивное и интенсивное. Для анализа: dY/Y=γ+α*dK/K+β*dL/L – часть уравнения после γ показывает экстенсивный рост, но только в том случае, если имеет место постоянная отдача от масштаба производства.

Прирост объема производства определяется приростом капитала с коэффициентом эластичности α и труда с β: .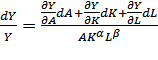

Для этой функции α и α-1 указывают доли фонда накопления и потребления в общем выпуске, при которых обеспечивается максимизация текущей величины чистой прибыли. Доказательство вытекает из теории предельной полезности (т.к. предельная производительность и капиталоотдача соответствуют реальным ценам на соответствующие факторы производства).

Рассмотрим производственную функцию Кобба-Дугласа: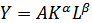

Где Y-объем производства, К-затраты капитала, L-затраты труда.

Показатели 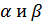являются коэффициентами частной эластичности объема производства Y соответственно по затратам капитала K и труда L.Учитывая влияние случайных возмущений, присущих каждому экономическому явлению, функцию Кобба-Дугласа можно представить в виде: 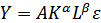. Так как 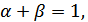имеем: 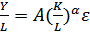, получаем зависимость производительности труда (Y/L) от капиталовооруженности (K/L). Для оценки параметров модели путем логарифмирования приводим ее к виду: 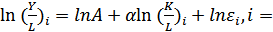1,…,n

ПФ Кобба-Дугласа задается выражением: 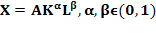, где А – коэф. нейтрального технич. прогресса; и 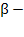коэф. эластичности выпуска по ОПФ и труд. ресурсам соотв. a – показывает на сколько % увеличится объем про-ва при увел. К на 1% при условии что L – не изменится. Аналогично 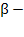к-т эласт-ти для L.

Если продифференцировать X по K и L, приходим к формулам эластичности:

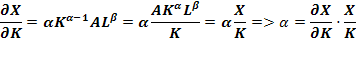
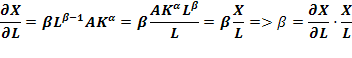
Если сумма показателей степени (α + β) =1, то функция Кобба — Дугласа явл.лин. однородной, то есть она демонстрирует пост.отдачу при изменении масштабов про-ва. Если сумма показателей степени >1, функция отражает возрастающую отдачу, а если <1, — убывающую.