Система «минимум–максимум»

Параметры системы «минимум—максимум» рассчитываются аналогично параметрам системы с установленной периодичностью пополнения запасов до постоянного уровня.

Порядок работы системы. Система «минимум—максимум» используется в случаях высокой стоимости оформления заказа (стоимости доставки). Заказ производится при условии, что запас в установленный момент времени (на границе интервала) находится на пороговом уровне или ниже его. В случае подачи заказа его размер рассчитывается так, чтобы поставка пополнила запас до максимального желательного уровня.

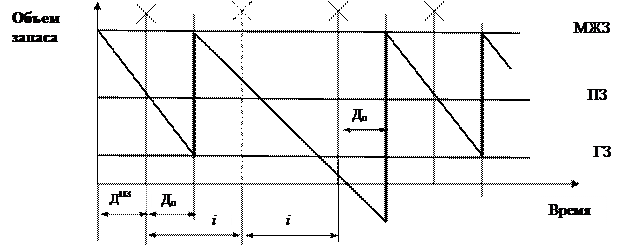Рис. 5.8. Работа системы «минимум-максимум»

в условиях кратковременного спада потребления (спроса)

Графически работа системы «минимум—максимум» представлена на рисунках 5.8 и 5.9.

Система «минимум—максимум» реагирует на сбои в поставках, поскольку фиксированным параметром системы является интервал времени между заказами, и в механизме ее функционирования заложена возможность определять величину каждого заказа расчетным путем.

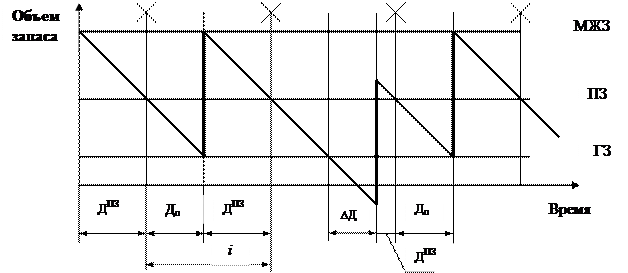Рис. 5.9. Работа системы «минимум–максимум»

в условиях однократного сбоя поставок

Порядок определения момента выдачи заказа в системе позволяет учесть возможные изменения потребления (система содержит пороговый уровень). Модель работы системы в условиях наличия сбоев в потреблении предполагает, что изменение интенсивности потребления происходит каждый цикл работы системы.

5.5. Система с фиксированным размером заказа

при постепенном пополнении запасов

Используя базовую модель системы с фиксированным размером заказа, мы предполагаем, что каждый заказ доставляется в один прием (единовременное пополнение запаса). Однако в некоторых случаях (например, когда предприятие является одновременно производителем и потребителем, или когда поставки рассредоточены во времени) запасы пополняются постепенно, а не мгновенно [10, с. 570-572].

Если темпы потребления и производства (или поставки) одинаковы, то запасы создаваться вообще не будут, поскольку весь выпуск сразу же используется. В этом случае вопрос об объеме партии заказа не встает. Чаще бывает, что темп производства или поставки превышает темпы потребления. Подобная ситуация изображена на рисунке 5.10.

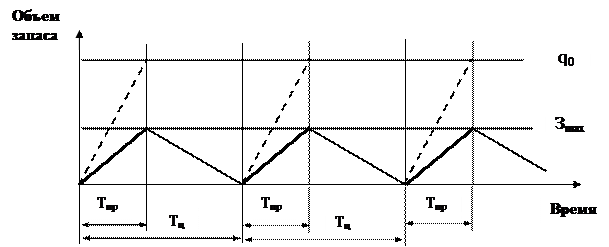Рис. 5.10. Система с фиксированным размером заказа

при постепенном пополнении запасов

В случае постепенного пополнения запасов товары производятся в течение только части цикла, потому что темпы производства выше темпов потребления; а потребление происходит на протяжении всего цикла. Во время производственной фазы цикла создаются запасы. Их уровень равен разнице между уровнем производства и уровнем потребления. Пока продолжается производство, уровень запасов будет повышаться. Когда производство остановится, уровень запасов начнет понижаться. Следовательно, уровень запасов будет максимальным в момент прекращения производства. Когда наличный запас будет исчерпан, производство возобновляется, и весь цикл повторяется.

Когда компания сама производит изделие, то у нее нет расходов на заказ как таковых. Однако для каждой производственной партии существуют расходы на подготовку производства (стоимость подготовки оборудования к данному производственному процессу: чистка, наладка, замена инструментов и т.п.) Расходы на подготовку производства в данном случае аналогичны расходам, связанным с заказом (доставкой), – то есть условно-постоянны в расчете на одну производственную партию, поскольку не зависят от размера партии. Аналогично и их использование в расчетах.

Общие расходы, связанные с созданием и содержанием запаса, составят:

С_общ = С_{хранения} + С_{подготовки производства}, (5.16)

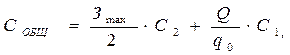(5.17)

где З_max – максимальный уровень запасов;

С₂ – издержки на хранение единицы запаса в течение периода;

Q – программа выпуска за период;

q₀ – экономичный объем (оптимальный размер) производственной партии.

С₁ – издержки на подготовку производства одной партии.

Максимальный уровень запасов определяется по формуле:

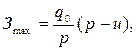(5.18)

где р – темп производства, ед./день;

и – темп потребления, ед./день;

(р – и) – прирост запаса, ед.

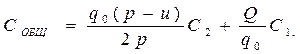
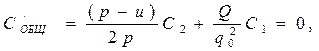
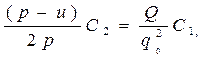
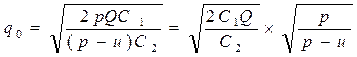. (5.19)

Продолжительность цикла (время потребления) определяется по формуле:

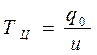. (5.20)

Продолжительность производства:

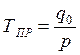. (5.21)

Количественные скидки

Количественные скидки — это элемент системы ценообразования, предполагающий снижение цены на товар при закупке крупных партий товара [10, с. 572-578].

Если скидки не предоставляются, цена всех единиц товара, приобретаемых за период, одинакова, и, соответственно, затраты на закупку не зависят от размера партии. Таким образом, в общем случае при определении оптимального размера заказа в составе общих затрат учитываются только затраты на хранение запаса и затраты на доставку, а оптимальный размер партии определяется по формуле (1).

В случае, когда поставщик предоставляет количественные скидки, размер заказываемой партии влияет на цену единицы товара, а через нее – на величину затрат на закупку и общих затрат, связанных с созданием и содержанием запаса (в расчете на период). Общие затраты при этом определяются как сумма затрат на хранение среднего остатка запаса в течение периода; затрат, связанных с заказом (доставкой), и затрат на закупку (стоимости приобретения общей потребности в товаре):

С_общ = С_{хранения} + С_{доставки} + С_{закупки}, (5.21)

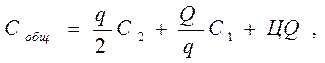(5.22)

где Ц — закупочная цена единицы товара.

Если предлагаются количественные скидки, то для каждой закупочной цены имеется отдельная кривая общих расходов на создание и содержание запаса. Включение стоимости закупки в состав общих расходов просто равномерно поднимает кривую С_общ на определенное значение. Тем не менее, поскольку закупочные цены различны, каждая кривая поднимается на разный уровень: меньшая закупочная цена поднимет кривую общих расходов на меньший уровень, чем более высокая закупочная цена. Кроме того, ни одна кривая не относится ко всем возможным значениям объема партии; каждая кривая относится только к части диапазона значений (рисунок 5.11).

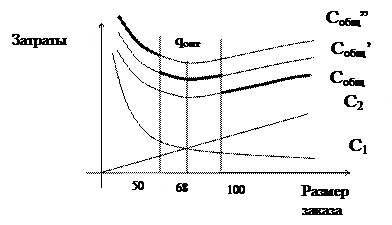
Рис. 5.11. Кривая общих расходов при постоянной

стоимости хранения

Реальным диапазоном данной ценымы будем называтьчасть кривой общих расходов, соответствующую тем значениям размера партии, которые действительно могут быть приобретены по данной цене, согласно условиям предоставления скидок. Следовательно, реальный показатель общих расходов сначала находится на кривой с максимальной закупочной ценой, а затем опускается вниз последовательно, кривая за кривой в точках изменения цены. Точки изменения цены — это минимальный объем заказа, необходимый для получения скидки. В результате получается кривая общих расходов, ступенчатая в точках изменения цены.

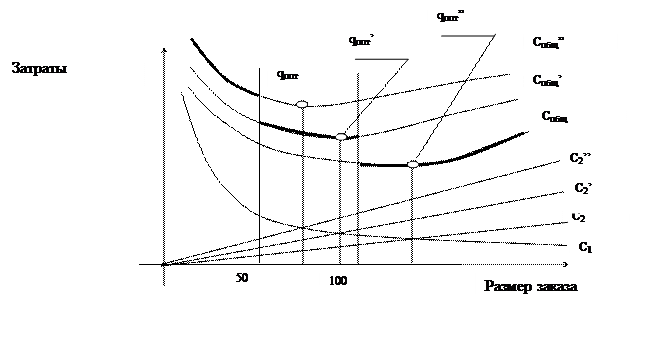
Даже если каждая кривая имеет свою точку минимума (рисунок 5.12), эти точки совершенно не обязательно реально применимы. Реальная кривая годовых общих расходов изображена жирной линией; только такие соотношения цены и объема закупок реальны. Цель модели количественных скидок — определение такого объема заказа, который даст минимальные общие расходы для всего набора кривых.

Существуют два основных варианта модели количественных скидок:

а) затраты на хранение единицы товара на предприятии (С₂) – постоянная величина;

б) затраты на хранение (С₂) определяются как процент от закупочной цены товара.

Если издержки хранения – постоянны, кривые общих затрат, соответствующие различным вариантам цены, будут иметь одинаковый наклон и различаться лишь уровнем своего расположения над осью абсцисс (рисунок 5.11). Точки минимума этих кривых будут соответствовать одному и тому же размеру заказа.

Рис. 5.12. Кривая общих расходов при стоимости хранения,

выраженной как процент от закупочной цены

Алгоритм действий при определении оптимального размера заказа по первому варианту модели количественных скидок (издержки хранения единицы изделия – постоянны):

1) рассчитайте величину q_опт, пользуясь формулой (5.1);

2) определите, в реальный диапазон какой цены попадает рассчитанное значение q_опт. Если это диапазон с наименьшей ценой, то найденное значение и будет оптимальным объемом заказа;

3) если цена, в реальном диапазоне которой находится рассчитанный q_опт не является наименьшей, то необходимо рассчитать величину общих затрат (С_общ) для данного q_опт и для всех точек изменения цены с меньшей ценой (то есть расположенных на графике правее данного q_опт). Сравните полученные показатели общих расходов. Наименьшее значение С_общ будет соответствовать оптимальному размеру партии.

Если издержки хранения определяются как процент от закупочной цены единицы изделия, то каждая кривая общих затрат будет иметь свою точку минимума (рис. 5.12).

Алгоритм действий при определении оптимального размера заказа по второму варианту модели количественных скидок (издержки хранения выражены процентом от закупочной цены):

1) рассчитайте величину q_опт для каждого варианта цены, пользуясь формулой (5.1);

2) определите, какие из полученных q_опт являются «реальными», то есть попадают в реальный диапазон той цены, для которой они рассчитаны. Например, на рисунке 5.12 реальными являются только q_опт’ и q_опт’’, так как q_опт с самой высокой ценой не попадает в свой реальный диапазон (с размерами партии до 49 единиц);

3) найдите реальный q_опт с самой меньшей ценой (то есть самый большой по размеру из реальных q_опт – на графике он расположен правее остальных реальных q_опт); рассчитайте величину общих затрат (С_общ) для данного q_опт и для всех точек изменения цены с меньшей ценой (то есть расположенных на графике правее данного q_опт). Сравните полученные показатели общих расходов. Наименьшее значение С_общ будет соответствовать оптимальному размеру партии.