Представление числовой информации в ЭВМ

В ЭВМ используются три вида чисел: с фиксированной точкой (запятой), с плавающей точкой (запятой) и двоично-десятичное представление.Точка (запятая) - это подразумеваемая граница целой и дробной частей числа.

У чисел с фиксированной точкой в двоичном формате предполагается строго определенное место точки (запятой). Обычно это место определяется или перед первой значащей цифрой числа, или после последней значащей цифрой числа. Если точка фиксируется перед первой значащей цифрой, то это означает, что число по модулю меньше единицы. Диапазон изменения значений чисел определяется неравенством

.

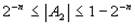Если точка фиксируется после последней значащей цифры, то это означает, что п - разрядные двоичные числа являются целыми. Диапазон изменения их значений составляет:

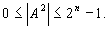
Перед самым старшим из возможных разрядов двоичного числа фиксируется его знак. Положительные числа имеют нулевое значение знакового разряда, отрицательные - единичные.

Другой формой представления чисел является представление их в виде чисел с плавающей точкой (запятой). Числа с плавающей точкой представляются в виде мантиссы т_a и порядка р_a , иногда это представление называют полулогарифмической формой числа. Например, число A₁₀ = 373 можно представить в виде 0.373 • 103, при этом т = 0.373, р = 3, основание системы счисления подразумевается фиксированным и равным десяти. Для двоичных чисел А₂ в этом представлении также формируется т_a и порядок р_a при основании системы счисления равным двум.

Порядок числа р_a определяет положение точки (запятой) в двоичном числе. Значение порядка лежит в диапазоне -р_a^max<=р_a<=р_a^max , где величина p_a^mах определяется числом разрядов r, отведенных для представления порядка

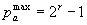
Положительные и отрицательные значения порядка значительно усложняют обработку вещественных чисел. Поэтому во многих современных ЭВМ используют не прямое значение р_a, а модифицированное р'_a приведенное к интервалу

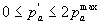
Значение р'_a носит название “характеристика числа”. Обычно под порядок (модифицированный порядок - характеристику) выделяют один байт. Старший разряд характеристики отводится под знак числа, а семь оставшихся разрядов обеспечивают изменение порядка в диапазоне

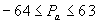
Модифицированный порядок р^'_a вычисляется по зависимости

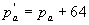
Этим самым значения р^'_a формируются в диапазоне положительных чисел

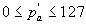
Мантисса числа m_a представляется двоичным числом, у которого точка фиксируется перед старшим разрядом, т. е.

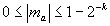
где k - число разрядов, отведенных для представления мантиссы.

Если

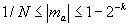
то старший значащий разряд мантиссы в системе счисления с основанием N отличен от нуля. Такое число называется нормализованным. Например, A₂ =(100;0.101101)₂ -нормализованное число А₂= 1011.01 или А₁₀= 11.25, а то же самое число А₂ = (101;0.0101101) - число ненормализованное, так как старший разряд мантиссы равен нулю.

Диапазон представления нормализованных чисел с плавающей точкой определяется

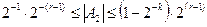
где r и k - соответственно количество разрядов, используемых для представления порядка и мантиссы.

Третья форма представления двоичных чисел - двоично-десятичная. Ее появление объясняется следующим. При обработке больших массивов десятичных чисел (например, больших экономических документов) приходится тратить существенное время на перевод этих чисел из десятичной системы счисления в двоичную для последующей обработки и обратно - для вывода результатов. Каждый такой перевод требует выполнения двух - четырех десятков машинных команд. С включением в состав отдельных ЭВМ специальных функциональных блоков или спецпроцессоров десятичной арифметики появляется возможность обрабатывать десятичные числа напрямую, без их преобразования, что сокращает время вычислений. При этом каждая цифра десятичного числа представляется двоичной тетрадой. Например, A₁₀=3759, A_2-10= 0011 0111 0101 1001. Положение десятичной точки (запятой), отделяющей целую часть от дробной, обычно заранее фиксируется. Значение знака числа отмечается кодом, отличным от кодов цифр. Например, “+” имеет значение тетрады “1100”, а “-” - “1101”.