Представление числовой информации с помощью систем счисления

2.1. Системой счисления (сс) называется совокупность приемов наименования и записи чисел

В любой сс для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами. Все остальные числа получаются в результате каких-либо операций из базисных чисел данной сс. Базисные числа (цифры) образуют алфавит сс. Количество различных цифр используемых в сс, называют ее основанием. СС различаются выбором базисных чисел и правилами образования из них остальных чисел.

Привычная нам сс является десятичной, позиционной. Для записи различных чисел в ней используется десять всем хорошо известных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а значение каждой цифры (её вес) определяется позицией, занимаемой этой цифрой в записи числа. Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево.

Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр. Если n<10 используются n первых арабских цифр, при n>10 к десяти арабским цифрам добавляют буквы. Например:

Основание	Название	Алфавит
n = 2	двоичная	0 1
n=3	троичная	0 1 2
n = 8	восьмеричная	0 1 2 3 4 5 6 7
n = 16	шестнадцатеричная	0 1 2 3 4 5 6 7 8 9 A B C D E F

В сс с основанием q(q – ичная сс) единицами разрядов служат последовательные степени числа q. q какого-либо разряда образуют единицу следующего разряда. Для записи числа в q – ичной сс требуется q различных знаков(цифр), изображающих базисные числа 0, 1,…, q-1. Запись числа q в q – ичной сс имеет вид 10, т.е. в любой сс её основание записывается как 10.

Развернутая форма записи основана на представлении этого числа в виде полинома:

A_q= 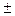(a_n-1q^n-1+a_n-2q^n-2+ . . . +a₀q⁰+a_-1q^-1+a_-2q^-2+ . . . +a_-mq^-m), где

A_q – само число, q – основание сс, а_i – цифры данной сс, n – число разрядов целой части числа, m – число разрядов дробной части числа.

Пример: Получить развернутую форму чисел 112₃, 15FC₁₆, 101,11₂.

112₃=1*10²+0*10¹+2*10⁰.

15FC₁₆=1*10³+5*10²+F*10¹+C.

101,11₂=1*10¹⁰+0*10¹+1*10⁰+1*10^-1+1*10^-10.

Перевод чисел в позиционных сс.

Перевод чисел в десятичную сс.

Перевод из недесятичной сс в десятичную переводится по следующему принципу. Если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе, равное данному.

Пример: Все числа из предыдущего примера перевести в десятичную систему.

112₃=1*3²+1*3¹+2*3⁰=9+3+2=14₁₀.

15FC₁₆=1*16³+5*16²+15*16¹+12=4096+1280+240+12=5628₁₀.

101,11₂=1*2²+0*2¹+1*2⁰+1*2^-1+1*2^-2=4+1+1/2+1/4=5,75₁₀.

Перевод десятичных чисел в другие сс.

Перевод целых чисел.

1. Основание новой сс выразить в десятичной сс и все последующие действия производить в десятичной сс.

2. Последовательно выполнять деление данного числа и получаемых неполных частных на основание новой СС до тех пор, пока не получим неполное частное, меньшее делителя.

3. Полученные остатки, являющиеся цифрами числа в новой СС, записать, начиная с последнего частного.

Перевод из десятичной с.с. в двоичную с.с.:

37ë2 36 18ë2_ а0= 1 18 9ë2 а1= 0 8 4ë2 а2=1 4 2ë2 а3=0 2 1=а5 a4=0   3710=1001012

Перевести десятичное число 315 в восьмеричную и 16-ричную СС.

315ë8 24 39ë8 75 39ë8 7232 4 3 7 31510=4738

315ë16 16 19ë16 155 16 1 144 3 31510=13В16, т.к. 1110=В16

Перевод дробной части.

1. Основание новой сс выразить в десятичной сс и все последующие действия производить в десятичной сс.

2. Необходимо последовательно умножать данное число и получаемые дробные части произведений на основание новой СС до тех пор, пока дробная часть произведения не станет равной 0 или не будет получена требуемая точность представления числа.

3. Полученные целые части произведения, являющиеся цифрами дробной частью числа в новой СС, записать, начиная с целой части первого произведения.

Пример. Перевести десятичную дробь 0,1875 в 2-,8-,16-ричную СС

	´ 2			´ 8				´ 16
	´ 2			´ 8
	´ 2
	´ 2

0,1875₁₀ = 0,0011₂ = 0,14₈=0,3₁₆

Перевод смешанных чисел.

Перевод смешанных чисел осуществляется в два этапа, Целая и дробная часть числа переводятся отдельно по соответствующим алгоритмам.

Пример. Из рассмотренных выше примеров следует :

315,1875₁₀=473,14₈=13В,3₁₆

Арифметика в позиционных сс.

Арифметические действия над числами в любой позиционной сс производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими полиномами. При этом нужно только пользоваться таблицами сложения и умножения однозначных чисел сложения и умножения, которые имеют место при данном основании q cc.

Например, таблицы сложения в 5-ричной сс:

+

х

Двоичная арифметика.

Таблица сложения.	Таблица вычитания.	Таблица умножение.
0 + 0 = 0	0 – 0 = 0	0 * 0 = 0
0 +1 = 1	1 – 0 = 1	0 * 1 = 0
1 + 0 = 1	1 – 1 = 0	1 * 0 = 0
1 + 1 = 10	10 –1 = 1	1 * 1 = 1

Тема2: Представление и кодирование информации в компьютере.

Кодирование.

Своя система существует и в ВТ- она называется двоичным кодированием и основана на представлении данных последовательностью всего двух знаков: 0 и 1. Эта связано с тем, что ЭВМ это электронное устройство для накопления и обработки информации, а работа электронных устройств основана на наличие или отсутствии электрического сигнала, т.е. различаются два устойчивых состояния «выключено»-0, «включено» -1. Эти знаки называются двоичными цифрами, или Binary digit(бит). Одним битом может .быть. выражены (закодированы два символа) два понятия: 0 или 1, двумя –четыре 00 01 10 11, тремя – восемь 000 001 010 011 100 101 110 111. Отсюда выводим, что, увеличивая на единицу количество разрядов в системе двоичного кодирования увеличивается в два раза количество значений, которое м.б. выражено в данной системе. Данную закономерность можно выразить формулой m=2ⁿ, где m-количество возможных значений,n-количество разрядов двоичного кодирования. Например, для кодирования целых чисел от 0 до 255 достаточно иметь 8 разрядов двоичного кодирования.