Представление текстовой информации в ЭВМ

Любое сообщение на любом языке состоит из последовательности символов — букв, цифр, знаков. Действительно, в каждом языке есть свой алфавит из определенного набора букв (например, в русском- 33 буквы, английском- 26, и т.д.). Из этих букв образуются слова, которые в свою очередь, вместе с цифрами и знаками препинания образуют предложения, в результате чего и создается текстовое сообщение. Не является исключением и язык, на котором «говорит» компьютер, только набор букв в этом языке является минимально возможным.

Стандартный набор из 256 символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией).

Он включает в себя большие и маленькие русские и латинские буквы, цифры, знаки препинания и арифметических действий и т.п.

Каждому символу ASCII соответствует 8-битовый двоичный код, например:

А — 01000001,

В — 01000010,

С — 01000011,

D — 01000100,

и т.д.

Таким образом, если человек создает текстовый файл и записывает его на диск, то на самом деле каждый введенный человеком символ хранится в памяти компьютера в виде набора из восьми нулей и единиц. При выводе этого текста на экран или на бумагу специальные схемы - знакогенераторы видеоадаптера (устройства, управляющего работой дисплея) или принтера образуют в соответствии с этими кодами изображения соответствующих символов.

Набор ASCII был разработан в США Американским национальным институтом стандартов (ANSI), но может быть использован и в других странах, поскольку вторая половина из 256 стандартных символов, т.е. 128 символов, могут быть с помощью специальных программ заменены на другие, в частности на символы национального алфавита, в нашем случае - буквы кириллицы.

Представление графической информации в ЭВМ.

Как и любая другая информация в ЭВМ, графические изображения хранятся, обрабатываются и передаются по линиям связи в закодированном виде - т.е. в виде большого числа бит - нулей и единиц. Существует большое число разнообразных программ, работающих с графическими изображениями. В них используются самые разные графические форматы- т.е. способы кодирования графической информации. Расширения имен файлов, содержащих изображение, указывают на то, какой формат в нем использован, а значит какими программами его можно просмотреть, изменить (отредактировать), распечатать.

Несмотря на все это разнообразие, существует только два принципиально разных подхода к тому, каким образом можно представить изображение в виде нулей и единиц (оцифровать изображение).

При использовании растровой графики с помощью определенного числа бит кодируется цвет каждого мельчайшего элемента изображения - пикселя. Каждый из пикселей имеет свой цвет, в результате чего и образуется рисунок, аналогично тому, как из большого числа камней или стекол создается мозаика или витраж, из отдельных стежков - вышивка, а из отдельных гранул серебра - фотография. При использовании растрового способа в ЭВМ под каждый пиксель отводится определенное число бит, называемое битовой глубиной. Каждому цвету соответствует определенный двоичный код (т.е. Код из нулей и единиц). Например, если битовая глубина равна 1, т.е. Под каждый пиксель отводится 1 бит, то 0 соответствует черному цвету, 1 -белому, а изображение может быть только черно-белым. Если битовая глубина равна 2. т.е. Под каждый пиксель отводится 2 бита, 00- соответствует черному цвету, 01- красному , 10 - синему ,11- черному, т.е. в рисунке может использоваться четыре цвета. Далее, при битовой глубине 3 можно использовать 8 цветов, при 4 - 16 и т.д. Поэтому, графические программы позволяют создавать изображения из 2, 4, 8, 16 , 32, 64, ... , 256, и т.д. цветов. Понятно, что с каждым увеличением возможного количества цветов (палитры) вдвое, увеличивается объем памяти, необходимый для запоминания изображения (потому что на каждый пиксель потребуется на один бит больше).

Основным недостатком растровой графики является большой объем памяти, требуемый для хранения изображения. Это объясняется тем, что нужно запомнить цвет каждого пикселя, общее число которых может быть очень большим. Например, одна фотография среднего размера в памяти компьютера занимает несколько мегабайт, т.е. Столько же, сколько несколько сотен (а то и тысяч) страниц текста. Для работы с растровой графикой используется в основном программа Adobe Photoshop.

При использовании векторной графики в памяти ЭВМ сохраняется математическое описание каждого графического примитива - геометрического объекта (например, отрезка, окружности, прямоугольника и т.п.), из которых формируется изображение. В частности, для построения окружности достаточно запомнить положение ее центра, радиус, толщину и цвет линии. По этим данным соответствующие программы построят нужную фигуру на экране дисплея. Понятно, что такое описание изображения требует намного меньше памяти (в 10 - 1000 раз) чем в растровой графике, поскольку обходится без запоминания цвета каждой точки рисунка. Одной из наиболее популярных программ векторной графики является Corel DRAW.

Вопросы для самоконтроля

1. Что означает термин "информатика" и каково его происхождение?

2. Какие области знаний и административно-хозяйственной деятельности официально закреплены за понятием "информатика" с 1978 года?

3. Какие сферы человеческой деятельности и в какой степени затрагивает информатика?

4. Назовите основные составные части информатики и основные направления её применения.

5. Что подразумевается под понятием "информация" в бытовом, естественно-научном и техническом смыслах?

6. Приведите примеры знания фактов и знания правил. Назовите новые факты и новые правила, которые Вы узнали за сегодняшний день.

7. От кого (или чего) человек принимает информацию? Кому передает информацию?

8. Где и как человек хранит информацию?

9. Что необходимо добавить в систему "источник информации — приёмник информации", чтобы осуществлять передачу сообщений?

10. Какие типы действий выполняет человек с информацией?

11. Приведите примеры ситуаций, в которых информация

а) создаётся;	д) копируется;	и) передаётся;
б) обрабатывается;	е) воспринимается;	к) разрушается;
в) запоминается;	ж) измеряется;	л) ищется;
г) делится на части;	з) принимается;	м) упрощается.

12. Приведите примеры обработки информации человеком. Что является результатами этой обработки?

13. Приведите примеры информации:

а) достоверной и недостоверной;

б) полной и неполной;

в) ценной и малоценной;

г) своевременной и несвоевременной;

д) понятной и непонятной;

е) доступной и недоступной для усвоения;

ж) краткой и пространной.

14. Назовите системы сбора и обработки информации в теле человека.

15. Приведите примеры технических устройств и систем, предназначенных для сбора и обработки информации.

16. От чего зависит информативность сообщения, принимаемого человеком?

17. Почему количество информации в сообщении удобнее оценивать не по степени увеличения знания об объекте, а по степени уменьшения неопределённости наших знаний о нём?

18. Как определяется единица измерения количества информации?

19. В каких случаях и по какой формуле можно вычислить количество информации, содержащейся в сообщении?

20. Почему в формуле Хартли за основание логарифма взято число 2?

21. При каком условии формула Шеннона переходит в формулу Хартли?

22. Что определяет термин "бит" в теории информации и в вычислительной технике?

23. Приведите примеры сообщений, информативность которых можно однозначно определить.

24. Приведите примеры сообщений, содержащих один (два, три) бит информации.[kgl]

[gl]ЛЕКЦИИ 2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ. СИСТЕМЫ СЧИСЛЕНИЯ.[:]

Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.

Существуют позиционные и непозиционные системы счисления.

В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позициив записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Сама же запись числа 757,7 означает сокращенную запись выражения

700 + 50 + 7 + 0,7 = 7 ^. 10² + 5 ^. 10¹ + 7 ^. 10⁰ + 7 ^. 10^—1 = 757,7.

Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.

За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

a_n-1 q^n-1 + a_n-2 q^n-2 + ... + a₁ q¹ + a₀ q⁰ + a_-1 q^-1 + ... + a_-m q^-m,

где a_i — цифры системы счисления; n и m — число целых и дробных разрядов, соответственно.
Например:

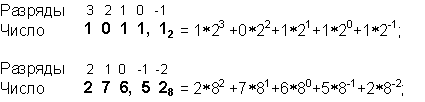
Целые числа в позиционных системах счисления.

В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.

Продвижением цифры называют замену её следующей по величине.

Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0.

Целые числа в любой системе счисления порождаются с помощью Правила счета:

Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.

Применяя это правило, запишем первые десять целых чисел

в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;

в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;

в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;

в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.

Какие системы счисления используют специалисты для общения с компьютером?

Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:

двоичная (используются цифры 0, 1);

восьмеричная (используются цифры 0, 1, ..., 7);

шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).

Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:

10-я 2-я 8-я 16-я

10-я 2-я 8-я 16-я A B C D E F

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.

Почему люди пользуются десятичной системой, а компьютеры — двоичной?

Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

представление информации посредством только двух состояний надежно и помехоустойчиво;

возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2.).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

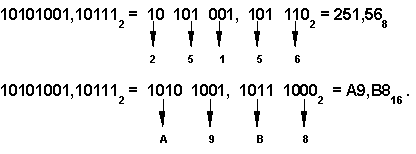
Перевод целых чисел из десятичной системы в любую другую позиционную систему счисления.

Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

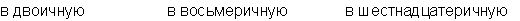
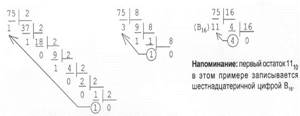
Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Пеpевод пpавильную десятичную дpобь в любую другую позиционную систему счисления.

Для перевода правильной десятичной дpоби F в систему счисления с основанием q необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q ^-(k+1) / 2.

Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

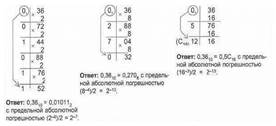
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.

Пеpевод чисел из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную.

Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16) в виде x_q = (a_na_n-1 ... a₀ , a_-1 a_-2 ... a_-m)_q сводится к вычислению значения многочлена

x₁₀ = a_n qⁿ + a_n-1 q^n-1 + ... + a₀ q⁰ + a_-1 q ^-1 + a_-2 q^-2 + ... + a_-m q^-m

средствами десятичной арифметики.

Примеpы:

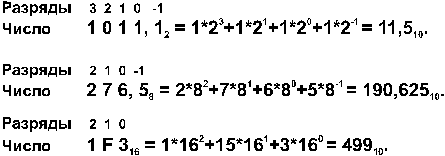
Сводная таблица переводов целых чисел из одной системы счисления в другую

Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную. Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рисунком:

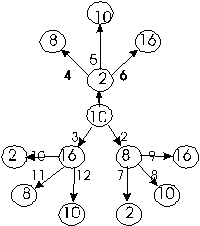
На этом рисунке использованы следующие обозначения:

в кружках записаны основания систем счисления;

стрелки указывают направление перевода;

номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице 4.1.

Например: 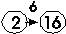означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.

Сводная таблица переводов целых чисел