Хроматическая дисперсия

Хроматическая дисперсия состоит из материальной и волноводной составляющих и имеет место при распространении как в одномодовом, так и в многомодовом волокне. Однако наиболее отчетливо она проявляется в одномодовом волокне из-за отсутствия межмодовой дисперсии.

Материальная дисперсия обусловлена зависимостью показателя преломления волокна от длины волны. В выражение для дисперсии одномодового волокна входит дифференциаль­ная зависимость показателя преломления от длины волны:

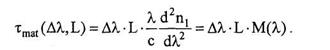(18)

Волноводная дисперсия обусловлена зависимостью коэффициента распространения моды от длины волны

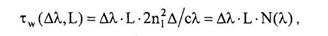(19)

где введены коэффициенты М(λ) и N ( λ ) – удельные материальная и волноводная дисперсии соответственно, а Δλ , (нм) – уширение длины волны вследствие некогерентности источника излучения. Результирующее значение коэффициента удельной хроматической дисперсии определяется как D ( λ ) = М(λ) + N ( λ ) . Удельная дисперсия имеет размерность пс/(нм·км). Если коэффициент волноводной дисперсии всегда больше нуля, то коэффициент материальной дисперсии может быть как положительным, так и отрицательным. И здесь важным является то, что при определенной длине волны (примерно 1310 ± 10 нм для ступенчатого одномодового волокна) происходит взаимная компенсация М(λ) и В(λ) , а результирующая дис персия D ( λ ) обращается в ноль. Длина волны, при которой это происходит, называется дли ной волны нулевой дисперсии λ0 . Обычно указывается некоторый диапазон длин волн, в пре­делах которых может варьироваться λ0 для данного конкретного волокна.

Фирма Corning использует следующий метод определения удельной хроматической дисперсии. Измеряются задержки по времени при распространении коротких импульсов све­та в волокне длиной" не меньше 1 км. После получения выборки данных для нескольких длин волн из диапазона интерполяции (800-1600 нм для MMF, 1200-1600 нм для SF и DSF) делает­ся повторная выборка измерения задержек на тех же длинах волн, но только на коротком эта­лонном волокне (длина 2 м). Времена задержек, полученных на нем, вычитаются из соответ­ствующих времен, полученных на длинном волокне.

Для одномодового ступенчатого и многомодового градиентного волокна используется эмпирическая формула Селмейера: τ(λ) = А + Вλ2 + С λ-2 . Коэффициенты А , В , С являются подгоночными, и выбираются так, чтобы экспериментальные точки лучше ложились на кривую τ(λ) , рисунок 7. Тогда удельная хроматическая дисперсия вычисляется по формуле:

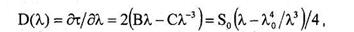(20)

где λ0 = (С/В)1/4 – длина волны нулевой дисперсии, новый параметр So =8В – наклон нулевой дисперсии (paзмepность пс/(нм2 ·км)), а λ – рабочая длина волны, для которой определяется удельная хроматическая дисперсия.

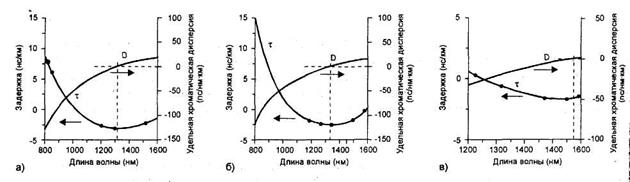Рисунок 7 – Кривые временных задержек и удельных хроматических дисперсий для: а) многомодового градиентного волокна (62,5/125);

б) одномодового ступенчатого волокна (SF);

в) одномодового волокна со смещенной дисперсией (DSF)

Поляризационная модовая дисперсия

Поляризационная модовая дисперсия τ pmd – возникает вследствие различной скорости распространения двух взаимно перпендикулярных поляризационных составляющих моды. Коэффициент удельной дисперсии Тнормируется в расчете на 1 км и имеет размерность (пс / 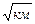), aτ pmd растет с ростом расстояния по закону 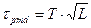. Для учета вклада в результирующую дисперсию следует добавить слагаемое 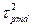в правую часть (15). Из-за небольшой величины τpmd может проявляться исключительно в одномодовом волокне, причем когда используется передача широкополосного сигнала (полоса пропускания 2,4 Гбит/с и выше) с очень узкой спектральной полосой излучения 0,1 нм и меньше. В этом случае хроматическая дисперсия становится сравнимой с поляризационной модовой дисперсией.

В одномодовом волокне в действительности может распространяться не одна мода, а две фундаментальные моды – две перпендикулярные поляризации исходного сигнала. В идеальном волокне, в котором отсутствуют неоднородности по геометрии, две моды распространялись бы с одной и той же скоростью, рисунок 8 а. Однако на практике волокна имеют не идеальную геометрию, что приводит к различной скорости распространения двух поляризационных составляющих мод, рисунок 8 б.

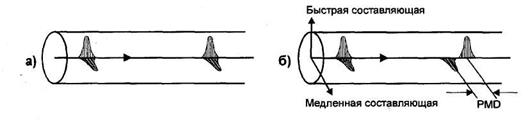Рисунок 8 – Появление поляризационной модовой дисперсии.

Избыточный уровень τ pmd , проявляясь вместе с чирпированным модулированным сигналом от лазера, а также поляризационной зависимостью потерь, может приводить к временным колебаниям амплитуды аналогового видеосигнала. В результате ухудшается качество изображения, или появляются диагональные полосы на телевизионном экране. При передаче цифрового сигнала высокой полосы (>2,4 Гбит/с) из-за наличия τ pmd может возрастать битовая скорость появления ошибок.

Главной причиной возникновения поляризационной модовой дисперсии является нециркулярность (овальность) профиля сердцевины одномодового волокна, возникающая в процессе изготовления или эксплуатации волокна. При изготовлении волокна только строгий контроль позволяет достичь низких значений этого параметра.

Ход работы:

РАСЧЕТ ПАРАМЕТРОВ ОПТИЧЕСКОГО ВОЛОКНА SM - 9/125 ФИРМЫ LUCENT TECHNOLOGIES

2.1 Расчет геометрических параметров оптоволокна

Числовую апертуру волокна рассчитаем по формуле (5). Подставив значения n 1 =1,466 , Δ=0,33 % , получим:

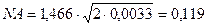
Далее из выражения (7) найдем нормированную частоту для окна прозрачности λ=1310 нм:

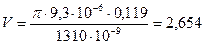
Таким образом, на длине волны 1310 нм (в соответствии с соотношением (8)) в волокне может существовать многомодовый режим, но, как уже говорилось выше, неосновные моды быстрее затухают и при помещении волокна в кабель, который при прокладке будет испытывать изгибы, неосновные моды вырождаются и в волокне будет одномодовый режим.

2.2 Определение длины волны отсечки

Как уже говорилось выше, различают волоконную и кабельную длину волны отсечки. Кабельная определяется экспериментально. Рассчитаем волоконную длину волны отсечки из выражения (12).

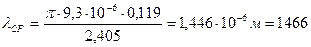нм

Учитывая, что кабельная длина волны отсечки смещена относительно волоконной в сторону более коротких длин волн, это еще раз подтверждает, что на длине волны 1310 нм в волокне, помещенном в кабель будет одномодовый режим.

2.3 Определение затухания в оптоволокне

Как уже писалось выше затухание в волокне складывается из собственных и кабельных потерь. Собственные потери определим из графика на рисунке 5.

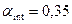дБ/км

Тогда кабельные потери можно определить, как

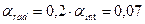дБ/км

Общее затухание в волокне составит

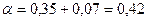дБ/км

Как видно из графика (рисунок 5) наименьшего значения этого показателя можно добиться при работе на длине волны 1550 нм.

2.4 Определение дисперсии и полосы пропускания волокна

Для одномодового режима модовая составляющая дисперсии обращается в 0 . Кроме того, как видно из рисунка 7 б, хроматическая дисперсия в окне прозрачности 1310 нм тоже равна 0 . Таким образом, в этом режиме в волокне будет присутствовать только поляризационная модовая дисперсия. Исходя из технических характеристик оптоволокна коэффициент поляризационной модовой дисперсии составляет Т=0,2 пс/√км. Тогда при расчете на L =100 км длины волокна, получим

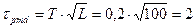пс

Далее из выражения (17) найдем полосу пропускания оптоволокна с расчетом на длину 100 км

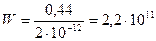Гц

С учетом того, что по техническим характеристикам оптоволокна коэффициент поляризационной модовой дисперсии не превышает значения 0,2 пс/√км, величина W =220 ГГц является минимальной полосой пропускания на расстоянии 100 км.

Содержание отчета:

Название, цель работы

Расчет параметров в соответствии с вариантом

Ответы на контрольные вопросы

Вывод.

Контрольные вопросы:

1. Виды одномодовых волокон

2. Факторы, влияющие на распространение света

3. Потери на рассеянии