Неравновероятные события

Тема: Подходы к понятию информации и её измерению. Принципы обработки информации компьютером. Алгоритмы и способы их описания

Информация. Информационные объекты различных видов

Информатика - это наука об организации процессов получения, хранения, обработки и передачи информации в системах различной природы. Информатика также изучает возможность автоматизации информационных процессов компьютерными средствами. Синонимом слова "компьютер" является "электронно-вычислительная машина" или ЭВМ. Персональный компьютер - один из видов компьютеров наряду с многопроцессорными и мультисистемными компьютерами. Сущность же компьютера - это транзисторная технология, которая реализована во всей современной радиотехнике. Более того, процессор как основа компьютера также не является уникальным явлением, так как процессоры сегодня могут иметь как телефоны, телевизоры, так и другие бытовые устройства.

Информация (в переводе с латинского informatio - разъяснение, изложение) - это ключевое понятие современной науки, которое стоит в одном ряду с такими как "вещество" и "энергия". Существует три основные интерпретации понятия "информация".

Научная интерпретация. Информация - исходная общенаучная категория, отражающая структуру материи и способы ее познания, несводимая к другим, более простым понятиям.

Абстрактная интерпретация. Информация - некоторая последовательность символов, которые несут как вместе, так в отдельности некоторую смысловую нагрузку для исполнителя.

Конкретная интерпретация. В данной плоскости рассматриваются конкретные исполнители с учетом специфики их систем команд и семантики языка. Так, например, для машины информация - нули и единицы; для человека - звуки, образы, и т.п.

Существуют несколько концепций (теорий) информации.

Первая концепция (концепция К. Шеннона), отражая количественно-информационный подход, определяет информацию как меру неопределенности (энтропию) события. Количество информации в том или ином случае зависит от вероятности его получения: чем более вероятным является сообщение, тем меньше информации содержится в нем.

Вторая концепция рассматривает информацию как свойство (атрибут) материи. Ее появление связано с развитием кибернетики и основано на утверждении, что информацию содержат любые сообщения, воспринимаемые человеком или приборами. Наиболее ярко и образно эта концепция информации выражена академиком В.М. Глушковым.

Третья концепция основана на логико-семантическом (семантика - изучение текста с точки зрения смысла) подходе, при котором информация трактуется как знание, причем не любое знание, а та его часть, которая используется для ориентировки, для активного действия, для управления и самоуправления. Иными словами, информация - это действующая, полезная, "работающая" часть знаний. Представитель этой концепции В.Г. Афанасьев.

В настоящее время термин информация имеет глубокий и многогранный смысл. Во многом, оставаясь интуитивным, он получает разные смысловые наполнения в разных отраслях человеческой деятельности:

- в житейском аспекте под информацией понимают сведения об окружающем мире и протекающих в нем процессах, воспринимаемые человеком или специальными устройствами;

- в технике под информацией понимают сообщения, передаваемые в форме знаков или сигналов;

- в теории информации (по К.Шеннону) важны не любые сведения, а лишь те, которые снимают полностью или уменьшают существующую неопределенность;

- в кибернетике, по определению Н. Винера, информация - эта та часть знаний, которая используется для ориентирования, активного действия, управления, т.е. в целях сохранения, совершенствования, развития системы;

- в семантической теории (смысл сообщения) - это сведения, обладающие новизной, и так далее...

Такое разнообразие подходов не случайность, а следствие того, что выявилась необходимость осознанной организации процессов движения и обработки того, что имеет общее название - информация.

Вероятностный подход к определению количества информации

В основе нашего мира лежат три состав­ляющие — вещество, энергия и информация. А как много в мире вещества, энергии и информации.

- Можно ли измерить количество вещества и как именно? (Вещество можно взвесить (в килограммах, гаммах и т.д.) на весах, определить его длину (в сантиметрах, в метрах и т.д.) с помощью линейки, найти его объем, применив соответствующие измерения и т.д.)

- Можно ли определить количество энергии? (Можно, например, найти количество тепловой энергии в Дж, электроэнергии в кВт/ч, и т.д.)

- Можно ли измерить количество информации и как это сделать?

Оказывается, информацию также можно измерять и находить ее коли­чество.

Существуют два подхода к измерению информации.

Один из них называется содержательный или вероятностный. Из назва­ния подхода можно сделать вывод, что количество информации зависит от ее содержания.

Упражнение 1 (устно)

Определите количество информации в следующих сообщениях с позиции «много» или «мало».

1) Столица России — Москва.

2) Сумма квадратов катетов равна квадрату гипотенузы.

3) Дифракцией света называется совокупность явлений, которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженной оптической неоднородностью.

4) Эйфелева башня имеет высоту 300 метров и вес 9000 тонн.

Пояснение: содержит ли сообщение новые и понятные сведения.

Сообщение несет больше информации, если в нем содержатся новые и понятные сведения. Такое сообщение называется информативным.

Необходимо различать понятия информация и информативность.

- Содержит ли информацию учебник физики за 10 класс? (Да).

- Для кого он будет информативным - для ученика 10 класса или 1 класса? (Для ученика 10 класса он будет информативным, так как в нем содержится новая и понятная ему информация, а для ученика 1 класса она информативной не будет, так как информация для него непонятна.)

Вывод: количество информации зависит от информативности.

Количество информации в некотором сообщении равно нулю, если оно с точки зрения конкретного человека неинформативно. Количество информации в информативном сообщении больше нуля.

Но информативность сообщения сама по себе не дает точного определе­ния количества информации. По информативности можно судить только о том, много информации или мало.

3. Введение понятия вероятностного подхода в измерении инфор­мации

Рассмотрим понятие информативности с другой стороны. Если некото­рое сообщение является информативным, следовательно, оно пополняет нас знаниями или уменьшает неопределенность наших знаний. Другими словами сообщение содержит информацию, если оно приводит к уменьше­нию неопределенности наших знаний.

Рассмотрим пример

Мы бросаем монету и пытаемся угадать, какой стороной она упадет на поверхность. Возможен один результат из двух: монета окажется в положении «орел» или «решка». Каждое из этих двух событий окажется равновероятным, т.е. ни одно из них не имеет преимущества перед другим.

Перед броском монеты мы точно не знает, как она упадет. Это событие предсказать невозможно, т.е. перед броском существует неопределенность нашего знания (возможно одно событие из двух). После броска наступает полная определенность знания, т.к. мы получаем зрительное сообщение о положении монеты. Это зрительное сообщение уменьшает неопределен­ность нашего знания в два раза, т.к. из двух равновероятных событий произошло одно.

Если мы кидаем шестигранный кубик, то мы также не знаем перед брос­ком, какой стороной он упадет на поверхность. В этом случае, возможно, получить один результат из шести равновероятных. Неопределенность знаний равна шести, т.к. именно шесть равновероятных событий может произойти. Когда после броска кубика мы получаем зрительное сообщение о результате, то неопределенность наших знаний уменьшается в шесть раз.

Упражнение 2 (устно)

Еще один пример. На экзамен приготовлено 30 билетов. Чему равно количество событий, которые могут произойти при вытягивании билета? (30)

- Равновероятны эти события или нет? (Равновероятны.)

- Чему равна неопределенность знаний студента перед тем как он вытянет билет? (30)

- Во сколько раз уменьшится неопределенность знания после того как студент билет вытянул? (В 30раз.)

- Зависит ли этот показатель от номера вытянутого билета? (Нет, т.к. события равновероятны.)

Из всех рассмотренных примеров можно сделать следующий вывод:

Чем больше начальное число возможных равновероятных событий, тем в большее количество раз уменьшается неопределенность наших знаний, и тем большее количество информации будет содержать сообщение о результатах опыта.

А каким может быть самое маленькое количество информации? Вернем­ся к примеру с монетой. Предположим, что у монеты обе стороны «орел».

- Существует ли неопределенность знаний пред броском в этом случае? Почему? (Нет, так как мы заранее знаем, что выпадет в любом случае «орел».)

- Получите вы новую информацию после броска? (Нет, так как ответ мы уже знали заранее.)

- Будет ли информативным сообщение о результате броска? (Нет, так оно не принесло новых и полезных знаний.)

- Чему равно количество информации в этом случае? (Нулю, т.к. оно неинформативно.)

Вывод: мы не получаем информации в ситуации, когда происходит одно событие из одного возможного. Количество информации в этом случае равно нулю.

Для того чтобы количество информации имело положительное значение, необходимо получить сообщение о том, что произошло событие как минимум из двух равновероятных. Такое количество информации, кото­рое находится в сообщении о том, что произошло одно событие из двух равно­вероятных, принято за единицу измерения информации и равно 1 биту.

Огромное количество способов кодирования информации неизбежно привело пытливый ум человека к попыткам создать универсальный язык или азбуку для кодирования. Эта проблема была достаточно успешно реализована лишь в отдельных областях техники, науки и культуры. Своя система кодирования информации существует и в вычислительной технике. Она называется двоичным кодированием. Всю информацию, с которой работает вычислительная техника, можно представить в виде последовательности всего двух знаков – 1 и 0. Эти два символа называются двоичными цифрами, по-английски – binary digit или сокращенно bit – бит.

1 бит кодирует 2 понятия или сообщения (0 или 1)

2 бита – 4 разных сообщения (00 или 01 или 10 или 11)

3 бита – 8 разных сообщений

4 бита – 16 разных сообщений и т.д.

Общая формула

,

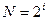где N – количество значений информации, i – количество бит.

Почему именно двоичное кодирование используется в вычислительной технике? Оказывается такой способ кодирования легко реализовать технически: 1 – есть сигнал, 0 – нет сигнала. Для человека такой способ кодирования неудобен тем, что двоичные последовательности получаются достаточно длинными. Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.

Итак, с помощью битов информация кодируется. С точки зрения коди­рования с помощью 1 бита можно закодировать два сообщения, события или два варианта некоторой информации. С точки зрения вероятности 1 бит — это такое количество информации, которое позволяет выбрать одно событие из двух равновероятных. Согласитесь, что эти два определения не противоречат друг другу, а совершенно одинаковы, но просто рассмотрены с разных точек зрения.

Еще одно определение 1 бита:

1 бит - это количество информации, уменьшающее неопределенность знаний в два раза.

Игра «Угадай число»

Загадайте число из предло­женного интервала.

Стратегия поиска:

Необходимо на каждом шаге в два раза уменьшать неопределенность зна­ния, т.е. задавать вопросы, делящие числовой интервал на два. Тогда ответ «Да» или «Нет» будет содержать 1 бит информации. Подсчитав общее ко­личество битов (ответов на вопросы), найдем полное количество информа­ции, необходимое для отгадывания числа.

Например, загадано число 5 из интервала от 1 до 16 (неопределенность знаний перед угадыванием равна 16).

Вопрос	Ответ	Неопределенность знаний	Полученное количест­во информации
Число больше 8?	Нет		1 бит
Число больше 4?	Да		1бит
Число больше 6?	Нет		1бит
Число 5?	Да		1 бит
Итого:			4 бита

Вывод: количество информации, необходимое для определения одного из 16 чисел, равно 4 бита.

Существует формула, которая связывает между собой количество возможных событий и количество информации:

,

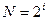где N — количество возможных вариантов, i - количество информации.

Пояснение: формулы одинаковые, только применяются с разных точек зрения - кодирования и вероятности.

Если из этой формулы выразить количество информации, то получится

.

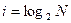Как пользоваться этими формулами для вычислений:

- если количество возможных вариантов N является целой степенью числа 2, то производить вычисления по формуле 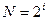достаточно легко. Вернемся к примеру: N = 32, i = 5, т.к. ;

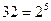- если же количество возможных вариантов информации не является целой степенью числа 2, т.е. если количество информации число ве­щественное, то необходимо воспользоваться калькулятором или сле­дующей таблицей.

Количество информации в сообщении об одном из N равновероятных событий: .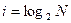

N	i	N	i	N	i	N	i
	0,00000		4,08746		5,04439		5,61471
	1,00000		4,16993		5,08746		5,64386
	1,58496		4,24793		5,12928		5,67243
	2,00000		4,32193		5,16993		5,70044
	2,32193		4,39232		5,20945		5,72792
	2,58496		4,45943		5,24793		5,75489
	2,80735		4,52356		5,28540		5,78136
	3,00000		4,58496		5,32193		5,80735
	3,16993		4,64386		5,35755		5,83289
	3,32193		4,70044		5,39232		5,85798
	3,45943		4,75489		5,42626		5,88264
	3,58496		4,80735		5,45943		5,90689
	3,70044		4,85798		5,49185		5,93074
	3,80735		4,90689		5,52356		5,95420
	3,90689		4,95420		5,55459		5,97728
	4,00000		5,00000		5,58496		6,00000

Например: Какое количество информации можно получить при угадыва­нии числа из интервала от 1 до 11? В этом примере N=11. Чтобы найти i (количество информации), необходимо воспользоваться таблицей. По таблице i = 3,45943 бит.

Упражнение 4 (устно)

1) Какое количество информации будет получено при отгадывании числа из интервала:

- от 1 до 64 - от 1 до 61 - от 1 до 20.

2) Какое количество информации будет получено после первого хода в игре «крестики-нолики» на поле:

- 3x3 - 4x4.

3) Сколько могло произойти событий, если при реализации одного из них получилось 6 бит информации.

Неравновероятные события

На самом деле рассмотренная нами формула является частным случаем, так как применяется только к равновероятным событиям. В жизни же мы сталкиваемся не только с равновероятными событиями, но и событиями, которые имеют разную вероятность реализации.

Например:

1. Когда сообщают прогноз погоды, то сведения о том, что будет дождь, более вероятно летом, а сообщение о снеге - зимой.

2. Если вы – лучший студент в группе, то вероятность сообщения о том, что за контрольную работу вы получили 5, больше, чем вероятность получения двойки.

3. Если на озере живет 500 уток и 100 гусей, то вероятность подстрелить на охоте утку больше, чем вероятность подстрелить гуся.

4. Если в мешке лежат 10 белых шаров и 3 черных, то вероятность достать черный шар меньше, чем вероятность вытаскивания белого.

5. Если одна из сторон кубика будет более тяжелой, то вероятность выпадения этой стороны будет меньше, чем других сторон.

Как вычислить количество информации в сообщении о таком событии?

Для этого необходимо использовать следующую формулу

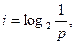
где i - это количество информации, р - вероятность события.

Вероятность события выражается в долях единицы и вычисляется по формуле:

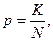
где К — величина, показывающая, сколько раз произошло интересующее нас событие, N — общее число возможных исходов какого-то процесса.

Задача №1

В мешке находятся 20 шаров. Из них 15 белых и 5 красных. Какое количество информации несет сообщение о том, что достали: а) белый шар; б) красный шар. Сравните ответы.

Решение:

1. Найдем вероятность того, что достали белый шар: рб = 15 / 20 = 0,75;

2. Найдем вероятность того, что достали красный шар: р = 5 / 20 = 0,25.

3. Найдем количество информации в сообщении о вытаскивании бело­го шара: 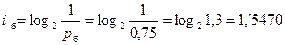бит.

4. Найдем количество информации в сообщении о вытаскивании красного шара: 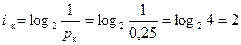бит.

Ответ: количество информации в сообщении о том, что достали белый шар, равно 1,1547 бит. Количество информации в сообщении о том, что достали красный шар, равно 2 бит.

При сравнении ответов получается следующая ситуация: вероятность вытаскивания белого шара была больше, чем вероятность вытаскивания красного шара, а информации при этом получилось меньше. Это не случай­ность, а закономерная, качественная связь между вероятностью события и количеством информации в сообщении об этом событии.

Задача №2

И коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вы­числите вероятность доставания кубика каждого цвета и количество ин­формации, которое при этом будет получено.

- Являются ли события равновероятными? Почему? (Нет, т.к. количество кубиков разное.)

- Какую формулу будем использовать для решения задачи?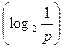
Решение:

1. Всего кубиков в коробке N = 10 + 8 + 5 + 12 = 35.

2. Найдем вероятности:

р_к = 10 / 35 ≈ 0,29,

р_з = 8/ 35 ≈ 0,22,

р_с = 12/35 ≈ 0,34,

р_ж = 5/35 ≈ 0,14.

3. Найдем количество информации:

i_c = log₂ (1/0,34) = log₂ 2,9 = 1,5360529 бит,

i_к = log₂ (1/0,29) = log₂ 3,4 = 1,7655347 бит,

i_з = log₂ (1/0,22) = log₂ 4,5 = 2,169925 бит,

i_ж = log₂ (l/0,14) = log₂ 7,l = 2,827819 бит.

Ответ: наибольшее количество информации мы получим при доставании желтого кубика по причине качественной связи между вероятностью и количеством информации.