Вероятностный подход к измерению количества информации

При вероятностном подходе предполагается, что существует обратная зависимость между величиной информации, содержащейся в сообщении о каком-либо событии и вероятностью осуществления этого события.

Предположим, что нас интересует следующая информация о студенте:

На каком из 5-ти курсов он учится?

В какой из 5-ти групп он числится?

Ответы на эти вопросы будут содержать одинаковое количество информации, так как являются равновероятными (р = 0,2). Сравним другие два вопроса:

На каком из 5-ти курсов он учится?

На какой форме обучения - по бюджету или контракту?

Ответ на первый вопрос содержит больше информации, чем на второй, так как вероятность правильного ответа на первый вопрос (р = 0,2) меньше вероятности правильного ответа на второй вопрос (р = 0,5).

Таким образом, на количество информации, получаемой из сообщения влияет фактор неожиданности его для получателя, зависящий от вероятности получения сообщения. Чем меньше эта вероятность, тем сообщение более неожиданно, и, следовательно, более информативно.

К данному выводу пришли исходя из следующих соображений.

Пусть имеется алфавит, состоящий из m символов. Как измерить количество информации (I), которое можно передать при помощи этого алфавита?

Было предложено принять в качестве меры количества информации число сообщений (N), которое можно передать при помощи этого алфавита. Например, пусть алфавит состоит из двух символов: а и b (m = 2). Сообщение может содержать разное число символов (п). Если сообщение содержит один символ (n = 1), то возможное число сообщений будет N = 2, при п = 2 N = 2 =4, при п = 3 N = 2 = 8 (таблица).

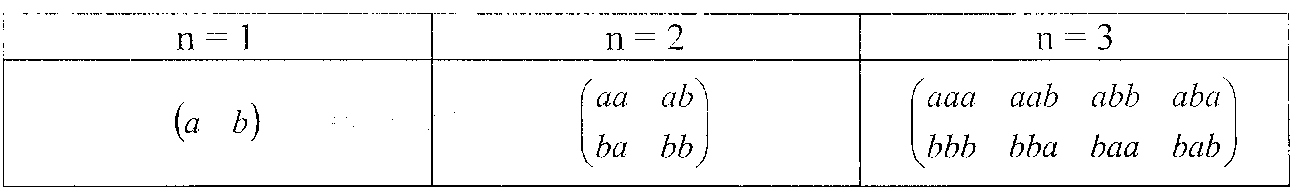
Анализируя таблицу, видим, что общее число сообщений зависит от числа символов в алфавите (ш) и в самом сообщении (п), и находится по формуле N = in". Таким образом количество информации равно I = N = т".

Однако оказалось, что не всегда можно применить данный подход.

1)Пусть алфавит состоит из одного символа (m = 1). Тогда
I = N = lⁿ = 1, то есть количество информации отлично от нуля. Между
тем, при одном символе мы не получим никакой информации, так как
знаем, что может появится только этот символ, т.е. 1 = 0.

2)Если поступают сообщения из двух источников, то число
сообщений будет равно I = N = Nj • N₂. Между тем логичней
предположить, что информация из двух источников должна складываться,
а не перемножаться.

Указанные недостатки устранил Хартли (1928 г.), который предложит измерять информацию, приходящуюся на одно сообщение, логарифмом числа сообщений: I = log N.

Тогда в первом случае (т = 1, N =1) количество информации будет равно I = log 1=0. При двух алфавита количество информации будет равно I = log Ni • N₂ = log Ni + log N₂.

Таким образом, общее количество информации будет равно

I = log N = log m" = n • log m.

Далее Хартли предположил, что вероятность появления любого символа из алфавита одинакова и равна р = 1 / т. Тогда общее количество информации можно выразить через вероятность появления символов з сообщении

I = п • log m = n ■ log (1 / p) = - n • log p.

Количество информации, приходящееся на один символ будет равно

I = - log р.

Это формула Хартли в окончательном виде. Для использования этой формулы на практике необходимо задать единицу измерения количества информации. Поступили следующим образом. Рассмотрели ситуацию, когда возможны всего два несовместных равновероятных события -например, появление герба или цифры при подбрасывании монеты (р = 0,5). Взяли логарифм по основанию 2 и получили: I = - log₂(l/2) = 1. Полученную величину приняли за единицу количества информации и назвали бит (bit - англ. binary unit - двоичная единица).

Формулу Хартли можно применять только в случае одинаковой вероятности появления символов. Олнако известно, что вероятность появления букв алфавита в словах неодинакова. Поэтому Шеннон (1948 г.) предложил другую формулу:

где pi - вероятность появления i-ro символа в сообщении. В данном случае Н - это среднее количество информации, приходящееся на один символ.

Формула Хартли является частным случаем формулы Шеннона. Если

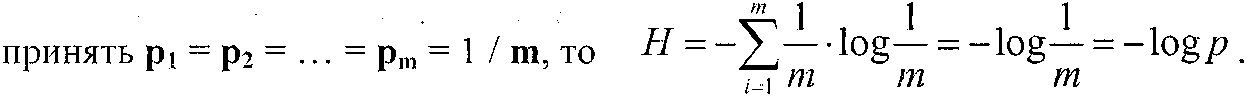
Величину Нназывают энтропией Шеннона. В теории информации энтропия - это мера неопределенности ситуации.

Чем больше энтропия системы, тем больше степень ее неопределенности. Поступающее сообщение полностью или частично снимает эту неопределенность. Следовательно, количество информации можно измерять тем, насколько понизилась энтропия системы после поступления сообщения.

Недостатком статистического подхода является то. что не всегда известны все вероятности. К тому же полностью игнорируется смысл, который несет информация. Например, сообщение «дважды два четыре» -это содержательное сообщение, часть таблицы умножения. А вот с точки зрения вероятностного подхода это сообщение не содержит никакой информации. Ведь вероятность того, что дважды два равно четыре, а не другому числу равна единице. Следовательно, сообщение содержит log? 1 = 0 бит информации. С этих позиций любая математическая теорема содержит нулевое количество информации.